Tứ giác nào sau đây vừa là hình chữ nhật, vừa là hình thoi?
Hình vuông vừa là hình chữ nhật, vừa là hình thoi.
Tứ giác nào sau đây vừa là hình chữ nhật, vừa là hình thoi?
Hình vuông vừa là hình chữ nhật, vừa là hình thoi.
Nhóm tứ giác nào có tổng số đo hai góc đối bằng 1800?
Nhóm tứ giác có tổng số đo hai góc đối bằng 1800 là: “Hình thang cân, hình chữ nhật, hình vuông.”
Cho hình chữ nhật ![]() . Trên tia đối của tia
. Trên tia đối của tia ![]() và
và ![]() lấy lần lượt hai điểm
lấy lần lượt hai điểm ![]() và
và ![]() sao cho
sao cho ![]() . Trên tia đối của tia
. Trên tia đối của tia ![]() lấy điểm
lấy điểm ![]() sao cho
sao cho ![]() . Tính tổng số đo hai góc
. Tính tổng số đo hai góc ![]() .
.
Hình vẽ minh họa
Theo giả thiết, và
, suy ra tứ giác
là hình bình hành.
Mặt khác
Vậy là hình chữ nhât.
Ta có:
Xét tai tam giác và có:
Mặt khác
Cho tam giác ![]() vuông cân tại
vuông cân tại ![]() . Trên các cạnh
. Trên các cạnh ![]() lấy lần lượt các điểm
lấy lần lượt các điểm ![]() sao cho
sao cho ![]() . Từ điểm
. Từ điểm ![]() vẽ
vẽ ![]() song song với
song song với ![]() . Tứ giác
. Tứ giác ![]() là hình gì?
là hình gì?
Hình vẽ minh họa
Ta có:
Tam giác vuông cân tại
nên
Do đó tam giác vuông tại
và
nên tam giác
là tam giác vuông cân tại
.
Mà . Và
Do đó là hình bình hành.
Hình bình hành có
Vậy là hình chữ nhật.
Cho hình bình hành ![]() , tia phân giác góc
, tia phân giác góc ![]() cắt tia phân giác góc
cắt tia phân giác góc ![]() và tia phân giác góc
và tia phân giác góc ![]() lần lượt tại
lần lượt tại ![]() , tia phân giác góc
, tia phân giác góc ![]() cắt
cắt ![]() lần lượt tại . Tứ giác
lần lượt tại . Tứ giác ![]() là hình gì?
là hình gì?
Hình vẽ minh họa
Gọi E là giao điểm của BP và CD, F là giao điểm của DQ và AB. Ta có:
(so le trong)
(hai góc đồng vị bằng nhau)
Chứng minh tương tự
Suy ra tam giác AFD cân tại A.
AQ là đường phân giác cũng là đường cao nên .
Vì theo trên nên suy ra
.
Chứng minh tương tự như trên, ta có .
Tứ giác MNPQ có bốn góc vuông nên MNPQ là hình chữ nhật.
Tìm x trong hình vẽ sau:

Hình vẽ minh họa:
Kẻ , ta có
là hình chữ nhật nên
Xét tam giác vuông tại H có
Cho hình vuông ![]() , trên các cạnh
, trên các cạnh ![]() lần lượt lấy
lần lượt lấy ![]() sao cho
sao cho ![]() . Chọn khẳng định đúng?
. Chọn khẳng định đúng?
Hình vẽ minh họa:
Bốn tam giác bằng nhau
=> Tứ giác là hình thoi.
Ta có:
Mặt khác
Vậy hình thoi có một góc vuông nên tứ giác
là hình vuông.
Cho tam giác ABC vuông tại A, M là một điểm thuộc cạnh BC. Qua M vẽ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC, AB theo thứ tự tại E và F. Xác định vị trí điểm M trên cạnh BC để tứ giác AFME là hình vuông?
Hình vẽ minh họa:
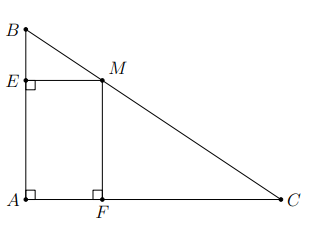
Tứ giác có
nên tứ giác AFME là hình chữ nhật.
Để tứ giác AFME là hình vuông thì đường chéo AM trở thành đường phân giác của góc
=> M là giao điểm của đường phân giác trong góc với BC.
Cho hình chữ nhật ![]() ,
, ![]() . Điểm M nằm trong hình chữ nhật. Tìm giá trị nhỏ nhất của tổng
. Điểm M nằm trong hình chữ nhật. Tìm giá trị nhỏ nhất của tổng ![]() .
.
Hình vẽ minh họa
Ta có ABCD là hình chữ nhật nên
Đặt
Xét ba điểm ta có:
Do đó hay
Mặt khác hay
Từ (*) và (**) suy ra
Dấu " = " xảy ra khi và chỉ khi M nằm giữa A và C và
=> M là trung điểm của AC
Chứng minh tương tự ta được:
Dấu “=” xảy ra khi M là trung điểm của BD
Hay
Do đó giá trị nhỏ nhất của tổng S là 100 khi M là giao điểm của hai đường chéo AC và BD.
Cho tam giác ![]() vuông tại
vuông tại ![]() . Gọi
. Gọi ![]() là đường phân giác của góc
là đường phân giác của góc ![]() , (
, (![]() thuộc
thuộc ![]() ), từ
), từ ![]() kẻ
kẻ ![]() và
và ![]() lần lượt vuông góc với
lần lượt vuông góc với ![]() và
và ![]() . Tứ giác
. Tứ giác ![]() là hình gì?
là hình gì?
Hình vẽ minh họa
Xét tứ giác có
Nên tứ giác là hình chữ nhật.
Mà AD là đường chéo đồng thời là đường phân giác nên tứ giác là hình vuông.
Tứ giác có 4 cạnh bằng nhau và 4 góc bằng nhau là:
Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
Cho hình vuông ![]() cân tại
cân tại ![]() , góc ở đáy bằng 750 và hình vuông
, góc ở đáy bằng 750 và hình vuông ![]() (các điểm
(các điểm ![]() nằm cùng phía đối với
nằm cùng phía đối với ![]() ). Xác định dạng của tam giác
). Xác định dạng của tam giác ![]() .
.
Hình vẽ minh họa
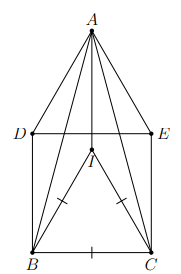
Vẽ tam giác đều vào trong hình vuông
Suy ra
Chứng minh tương tự
Vậy tam giác đều.
Cho hình thang vuông ![]() (
(![]() );
); ![]() . Vẽ
. Vẽ ![]() vuông góc
vuông góc ![]() tại
tại ![]() . trên tia đối của tia
. trên tia đối của tia ![]() lấy điểm
lấy điểm ![]() sao cho
sao cho ![]() . Gọi
. Gọi ![]() là giao điểm của
là giao điểm của ![]() và
và ![]() ,
, ![]() là trung điểm của
là trung điểm của ![]() . Vẽ
. Vẽ ![]() vuông góc
vuông góc ![]() . Tính số đo góc
. Tính số đo góc ![]() .
.
Trong tam giác , NK là đường trung bình, do đó
Dễ thấy tứ giác là hình chữ nhật, do đó N là trung điểm của AE và BD và
.
Tam giác IAE vuông tại I, có IN là đường trung tuyến, do đó: .
Tam giác IBD có IN là trung tuyến thỏa mãn , do đó BID là tam giác vuông tại I.
Chọn khẳng định sai?
Hình vuông vừa là hình chữ nhật và hình thoi nên nó có đầy đủ tính chất của hình chữ nhật và hình thoi.
Vậy khẳng định sai là: “Hình vuông là hình chữ nhật nhưng không là hình thoi”
Câu nào đúng trong các câu sau:
Trong hình thoi hai đường chéo vuông góc với nhau.
