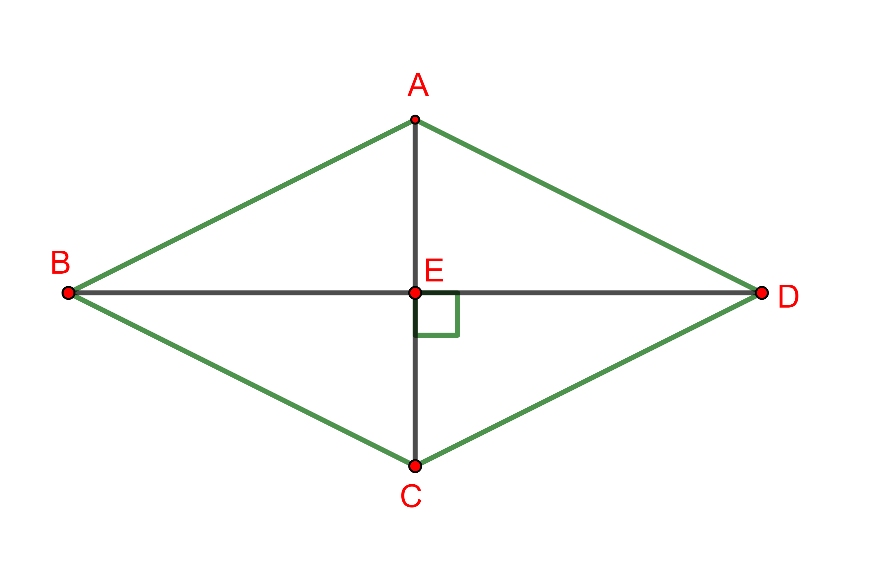
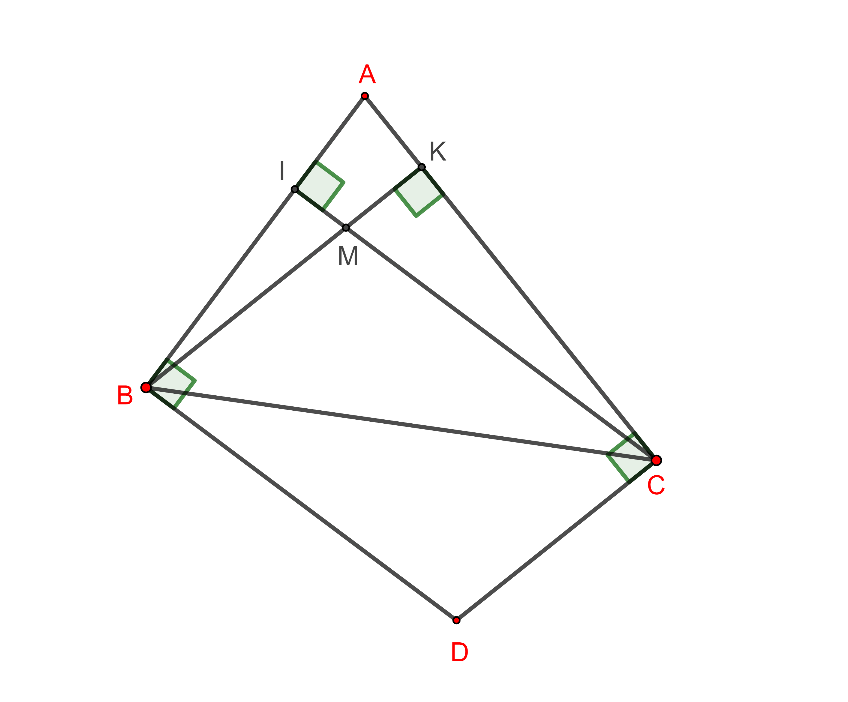
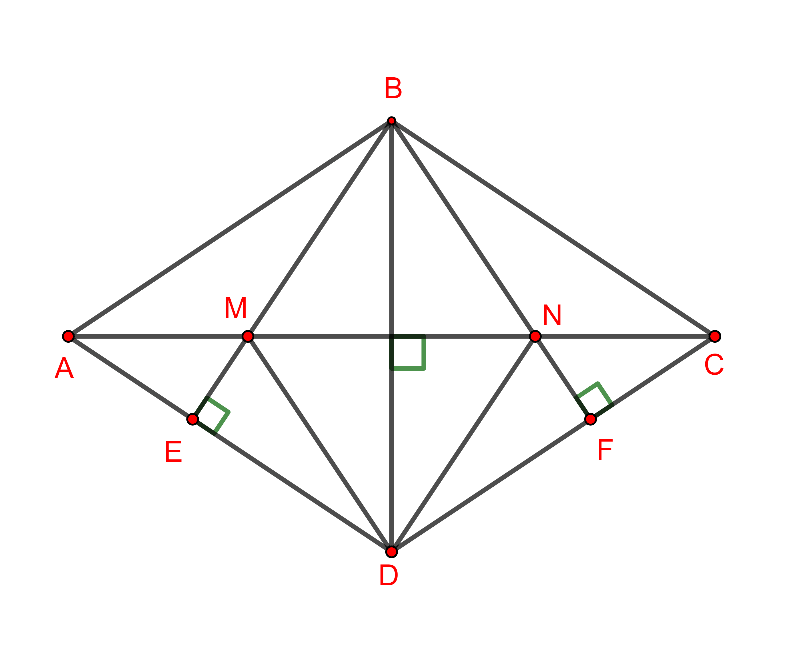
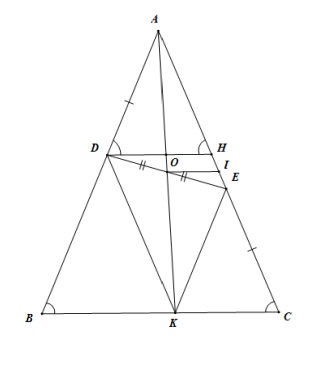
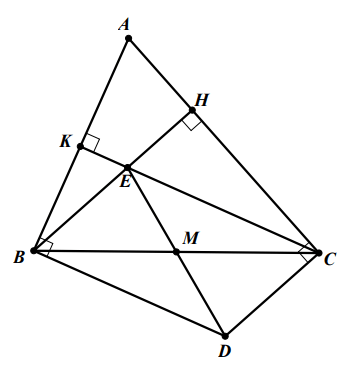
Cho tam giác ![]() có
có ![]() . Từ một điểm
. Từ một điểm ![]() bất kì trên cạnh
bất kì trên cạnh ![]() kẻ đường đường vuông góc với
kẻ đường đường vuông góc với ![]() , cắt tia đối của
, cắt tia đối của ![]() tại
tại ![]() , cắt
, cắt ![]() tại
tại ![]() . Tia phân giác của góc
. Tia phân giác của góc ![]() cắt
cắt ![]() và
và ![]() lần lượt tại
lần lượt tại ![]() và
và ![]() , tia phân giác góc
, tia phân giác góc ![]() cắt
cắt ![]() và
và ![]() lần lượt tại
lần lượt tại ![]() và
và ![]() . Tứ giác
. Tứ giác ![]() là hình gì?
là hình gì?
Hình vẽ minh họa
Gọi là giao điểm của
và
(cùng phụ với góc
)
Ta có:
Ta có: tam giác cân tại
=> Tam giác cân tại
Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường và hai đường chéo đó vuông góc với nhau nên
là hình thoi.