Lớp 8 Toán 8 - Chân trời sáng tạo

Ôn tập chương 7 Định lí Thalès trong tam giác CTST

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 15 câu
  • Điểm số bài kiểm tra: 15 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Vận dụng
    Tìm điều kiện để tứ giác là hình chữ nhật

    Cho tam giác ABC. Gọi D, E, F theo thứ tự là trung điểm của AB, BC, CA. Gọi M, N, P, Q theo thứ tự là trung điểm của AD, AF, EF, ED. Khi đó ΔABC có điều kiện gì thì MNPQ là hình chữ nhật?

    Hướng dẫn:

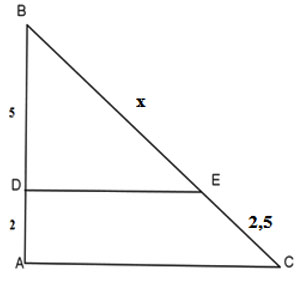
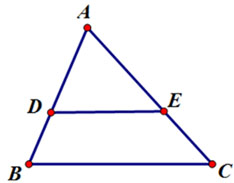
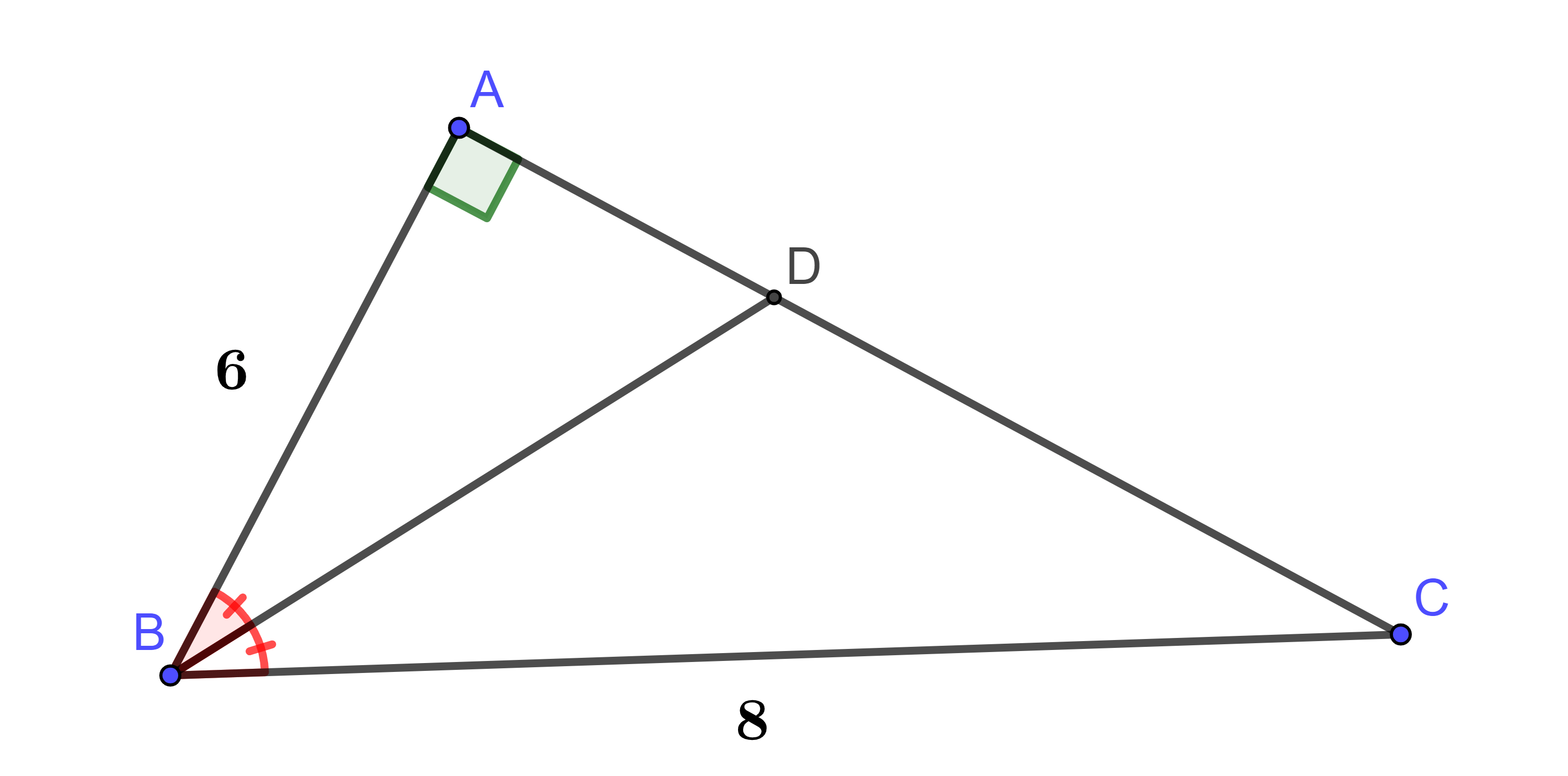
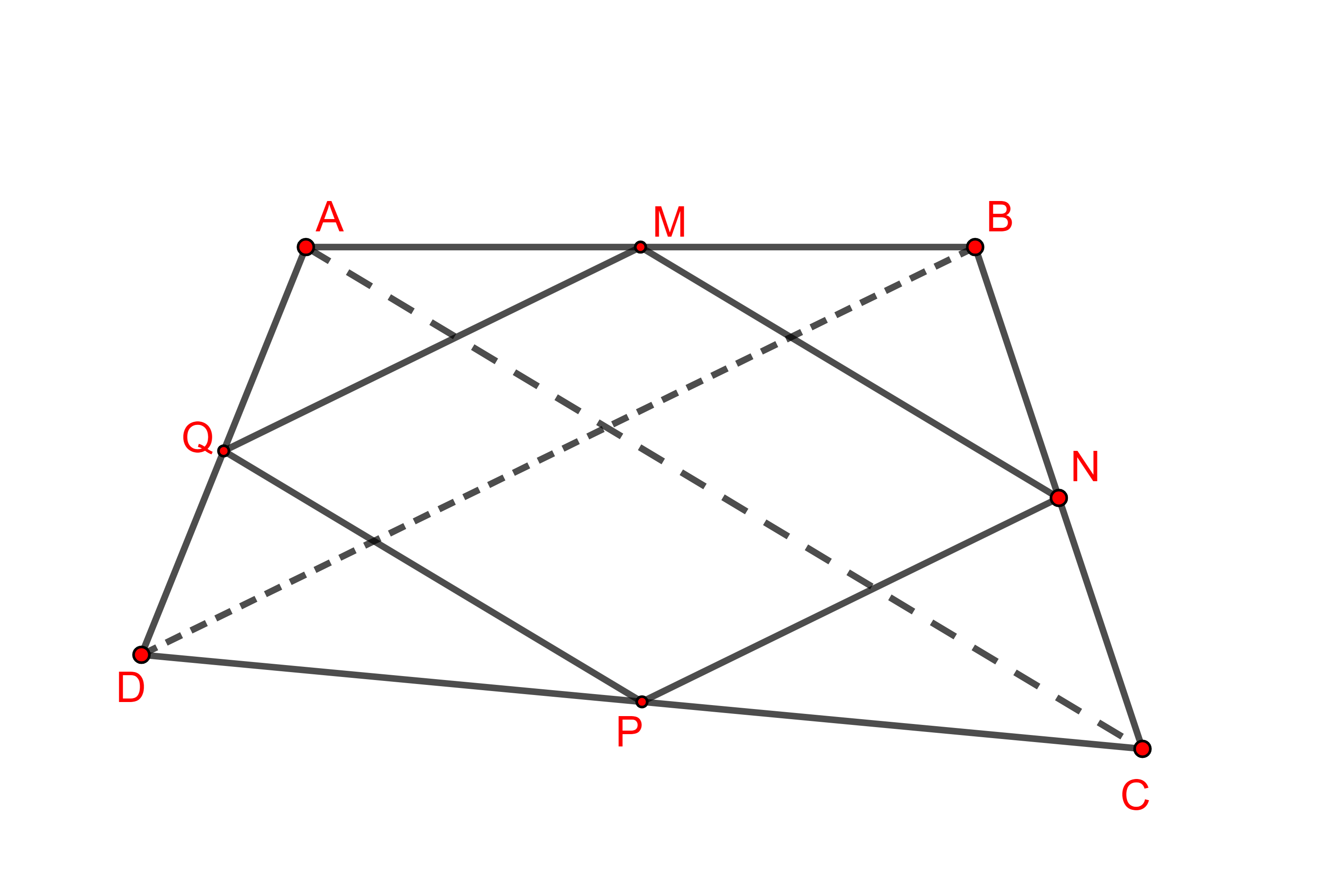
    Hình vẽ minh họa

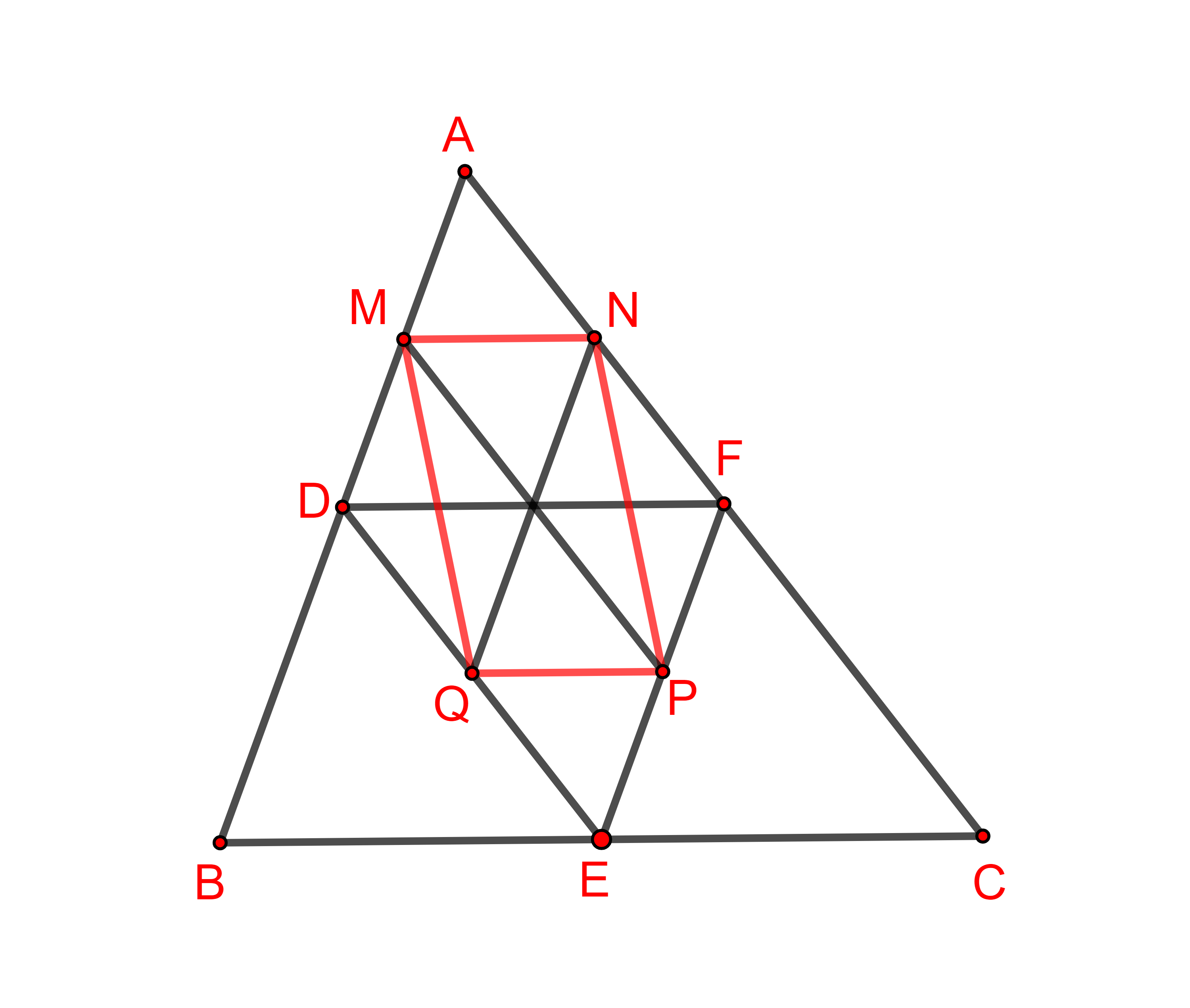
    Đường trung bình trong tam giác

    Xét ΔADE có:

    AM = MD; DQ = EQ

    => MQ là đường trung bình của ΔADE

    \Rightarrow \left\{ \begin{gathered} MQ//AE \hfill \\ MQ = \frac{1}{2}AE \hfill \\ \end{gathered} ight.

    Xét ΔAEF có:

    AN = NF; FP = PE (giả thiết)

    => NP là đường trung bình của ΔAEF

    \Rightarrow \left\{ \begin{gathered} NP//AE \hfill \\ NP = \frac{1}{2}AE \hfill \\ \end{gathered} ight.

    \Rightarrow \left\{ {\begin{array}{*{20}{l}} {MQ//NP\left( {//AE} ight)} \\ {MQ = NP\left( { = \dfrac{1}{2}AE} ight)} \end{array}} ight.

    Tứ giác MNPQ có:

    MQ // NP; MQ = NP

    => MNPQ là hình bình hành

    Để MNPQ là hình chữ nhật thì MN ⊥ PQ (1)

    Ta có: NP // AE (chứng minh trên) (2)

    Ta lại có: AM = MD, AN = NF (gt) => MN // DF

    Mặt khác: AD = DB, AF = FC (gt) => DF // BC

    Vậy MN // BC (3)

    Từ (1), (2), (3) suy ra: AE ⊥ BC

    Mà BE = EC (gt)

    Do đó ΔABC cân tại A (do AE vừa là đường cao, vừa là đường trung tuyến)

  • Câu 2: Thông hiểu
    Tính độ dài BC

    Cho tam giác ABC, phân giác trong kẻ từ đỉnh A cắt BC tại D. Biết rằng AB = \frac{1}{2}AC. Giả sử độ dài DC bằng 6cm khi đó độ dài cạnh BC là:

    Hướng dẫn:

    Áp dụng tính chất đường phân giác cho tam giác ABC, phân giác AD ta có:

    \frac{AB}{AC} = \frac{BD}{CD} \Rightarrow \frac{BD}{CD} = \frac{1}{2} \Rightarrow \frac{BD}{1} = \frac{CD}{2}

    \frac{BD}{1} = \frac{CD}{2} = \frac{BD + CD}{1 + 2} = \frac{BC}{3} (theo tính chất dãy tỉ số bằng nhau)

    \Rightarrow BC = \frac{3}{2}DC

    \Rightarrow BC = \frac{3}{2}.6 = 9(cm)

  • Câu 3: Nhận biết
    Tính độ dài AE

    Cho tam giác ABC, M là trung điểm của BC, AC =6cm. Gọi D là trung điểm của AM, E là giao điểm của DB và AC, F là trung điểm của EC. Tính độ dài AE.

    Hướng dẫn:

    Hình vẽ minh họa

    Xét tam giác BEM có BM = MC, EF = FC nên MF là đường trung bình của tam giác BEC.

    Do đó MF // BE

    Xét tam giác AMF có AD = CM, DE // MF nên DE là đường trung bình của tam giác AMF.

    Do đó AE = EF

    \Rightarrow AE = EF = FC

    \Rightarrow AE = \frac{1}{3}AC =\frac{1}{3}.6 = 2(cm)

  • Câu 4: Nhận biết
    Tính độ dài AB

    Cho hình vẽ:

    Định lí Thales

    Trong đó DE // BC, AE = 12, DB = 18, CA = 36. Độ dài AB bằng:

    Hướng dẫn:

    Ta có: DE // BC, theo định lý Thales ta có:

    \begin{matrix} \dfrac{{AE}}{{EC}} = \dfrac{{AD}}{{DB}} \Leftrightarrow \dfrac{{12}}{{36 - 12}} = \dfrac{{AD}}{{18}} \hfill \\ \Leftrightarrow \dfrac{{12}}{{24}} = \dfrac{{AD}}{{18}} \Leftrightarrow AD = \dfrac{{18.12}}{{24}} = 9\left( {cm} ight) \hfill \\ \Rightarrow AB = AD + DB = 9 + 18 = 27\left( {cm} ight) \hfill \\ \end{matrix}

  • Câu 5: Thông hiểu
    Tính tỉ số hai cạnh

    Cho hình thang ABCD; ( AB//CD ) có O là giao điểm của hai đường chéo. Đường thẳng qua O song song hai đáy và cắt AD, BC lần lượt tại E và F. Tính tỉ số \frac{{OE}}{{OF}}.

    Hướng dẫn:

    Hình vẽ minh họa

     

    Định lí Thales

    Áp dụng hệ quả của định lí Thales cho OE//DC, OF//DC và AB//DC ta được:

    \left\{ \begin{gathered} \dfrac{{OE}}{{DC}} = \dfrac{{AO}}{{AC}} \hfill \\ \dfrac{{OF}}{{DC}} = \dfrac{{BO}}{{DB}} \hfill \\ \dfrac{{AO}}{{AC}} = \dfrac{{BO}}{{BD}} \hfill \\ \end{gathered} ight. \Rightarrow \dfrac{{EO}}{{DC}} = \dfrac{{OF}}{{DC}} \Rightarrow OE = OF

    Vậy \frac{{OE}}{{OF}} =1

  • Câu 6: Thông hiểu
    Tính độ dài cạnh AD

    Cho tam giác ABC có \widehat A = {90^0}. Tia phân giác góc B cắt AC tại D. Biết AB = 6cm, AC = 8cm. Tính độ dài AD?

    Hướng dẫn:

    Hình vẽ minh họa

    Tính chất đường phân giác

    Xét tam giác ABC vuông tại A, áp dụng định lý Pythagore ta có:

    B{C^2} = A{B^2} + A{C^2}

    BD là tia phân giác góc B 

    => \frac{{DA}}{{DC}} = \frac{{AB}}{{BC}} = \frac{6}{{10}} = \frac{3}{5}

    \Rightarrow \frac{{DA}}{3} = \frac{{DC}}{5}

    Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

    \Rightarrow \frac{{DA}}{3} = \frac{{DC}}{5} = \frac{{DA + DC}}{{3 + 5}} = \frac{{AC}}{8} = \frac{8}{8} = 1 

    => DA = 3.1 = 3; DC = 5.1 = 5(cm)

    Vậy AD = 3.

  • Câu 7: Nhận biết
    Chọn khẳng định đúng

    Cho tam giác ACE có AC = 12cm. Lấy điểm B trên cạnh AC sao cho BC = 6cm. Lấy điểm D trên cạnh AE sao cho BD // EC. Chọn khẳng định đúng.

    Hướng dẫn:

    Xét tam giác ACE có: BD//CE

    Khi đó theo định lí Thalès ta có: \frac{DE}{AE} = \frac{BC}{AC} = \frac{6}{12} = \frac{1}{2}

  • Câu 8: Thông hiểu
    Xác định giá trị x trong hình vẽ

    Cho hình vẽ sau:

    Tìm giá trị của x?

    Hướng dẫn:

    Ta có:

    GH = FG - FH = 12,5 - 3,5 = 9(cm)

    Lại có EH là phân giác trong của góc E

    Áp dụng tính chất đường phân giác của góc E ta có:

    \frac{EF}{EG} = \frac{FH}{GH} \Rightarrow \frac{6,3}{x} = \frac{3,5}{9} \Rightarrow x = 16,2(cm)

  • Câu 9: Nhận biết
    Tìm đáp án đúng

    Cho hình vẽ sau:

    Biết AE là phân giác ngoài của góc \widehat{CAB}. Khẳng định nào sau đây đúng?

    Hướng dẫn:

    Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy nên

    \frac{AB}{AC} = \frac{BE}{CE}

  • Câu 10: Thông hiểu
    Tính độ dài EF

    Trong hình thang ABCD; (AB // CD) có AB = 28cm,CD = 70cm,AD = 35cm, vẽ một đường thẳng song song với hai cạnh đáy, cắt AD, BC theo thứ tự ở E và F. Tính độ dài EF biết rằng DE = 10cm.

    Hướng dẫn:

    Hình vẽ minh họa

    Theo giả thiết, vì DE = 10cm nên AE = 25cm.

    Gọi I là giao của AC và EF.

    Áp dụng định lí Thalès cho tam giác ACD nên ta có:

    \frac{AE}{AD} = \frac{EI}{DC} = \frac{AI}{AC} \Rightarrow \frac{25}{35} = \frac{EI}{70} \Rightarrow EI = 50

    Vì \frac{AI}{AC} = \frac{5}{7} \Rightarrow \frac{IC}{AC} = \frac{2}{7}

    Áp dụng định lí Thalès cho tam giác ABC ta có

    \frac{IC}{CA} = \frac{IF}{AB} \Rightarrow \frac{2}{7} = \frac{IF}{28} \Rightarrow IF = 8

    Vậy EF = 58cm

  • Câu 11: Vận dụng
    Tìm điều kiện của hai đường chéo AC và BD

    Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA. Hai đường chéo AC và BD phải thỏa mãn điều kiện gì để M, N, P, Q là bốn đỉnh của hình vuông.

    Hướng dẫn:

    Hình vẽ minh họa

    Hình vuông

    Xét tam giác ABD có: \left\{ {\begin{array}{*{20}{c}} {MA = MB} \\ {QA = QD} \end{array}} ight.

    => QM là đường trung bình của tam giác ABD.

    \Rightarrow \left\{ {\begin{array}{*{20}{c}} {QM//BD} \\ {QM = \dfrac{1}{2}BD} \end{array}} ight.\left( 1 ight)

    Tương tự ta cũng có NP là đường trung bình của tam giác BCD.

    \Rightarrow \left\{ {\begin{array}{*{20}{c}} {NP//BD} \\ {NP = \dfrac{1}{2}BD} \end{array}} ight.\left( 2 ight)

    Từ (1) và (2) suy ra MNPQ là hình bình hành (dấu hiệu nhận biết)

    Tương tự ta cũng có MN là đường trung bình của tam giác BAC \Rightarrow \left\{ {\begin{array}{*{20}{c}} {MN//AC} \\ {MN = \dfrac{1}{2}AC} \end{array}} ight.

    Để hình bình hành MNPQ là hình vuông

    \Rightarrow \left\{ {\begin{array}{*{20}{l}} {MN \bot NP} \\ {MN = NP} \end{array}} ight.

    Để {MN \bot NP} => AC ⊥ BD (vì MN // AC, NP // BD)

    Để {MN = NP} => AC = BD (vì \Rightarrow \left\{ \begin{gathered} MN = \dfrac{1}{2}AC \hfill \\ NP = \dfrac{1}{2}BD \hfill \\ \end{gathered} ight.)

    Vậy điều kiện cần để MNPQ là hình vuông là BD = AC; AC ⊥ BD

  • Câu 12: Nhận biết
    Chọn đáp án đúng

    Cho tam giác ABC có I, K lần lượt là trung điểm của AB và AC. Biết IK = 7cm. Ta có: 

    Hướng dẫn:

    Ta có:

    I, K là trung điểm của AB và AC 

    => IK là đường trung bình tam giác ABC

    \Rightarrow \left\{ \begin{gathered} IK//BC \hfill \\ IK = \frac{1}{2}BC \hfill \\ \end{gathered} ight. \Rightarrow BC = 2IK = 2.7 = 14\left( {cm} ight)

  • Câu 13: Thông hiểu
    Tính giá trị biểu thức

    Cho hình bên, biết DE // AC

    Định lí Thales

    Tính giá trị của x - 1

    Hướng dẫn:

    Theo bài ra ta có: DE // AC, áp dụng định lí Thales ta có:

    \begin{matrix} \dfrac{{BE}}{{BC}} = \dfrac{{BD}}{{BA}} \Leftrightarrow \dfrac{x}{{x + 2,5}} = \dfrac{5}{{5 + 2}} \hfill \\ \Leftrightarrow \dfrac{x}{{x + 2,5}} = \dfrac{5}{7} \Leftrightarrow 7x = 5x + 12,5 \hfill \\ \Leftrightarrow x = 6,25 \hfill \\ \end{matrix}

    Vậy x - 1 = 5,25

  • Câu 14: Nhận biết
    Chọn khẳng định đúng

    Cho tam giác ABC có đường phân giác trong AD. Kẻ đường phân giác ngoài AE của góc A. Chọn khẳng định đúng.

    Hướng dẫn:

    Hình vẽ minh họa

    Ta có AD là phân giác trong của tam giác ABC

    => \frac{DB}{DC} = \frac{AB}{AC}(*)

    Vì AE là phân giác ngoài của tam giác ABC nên \frac{EB}{EC} = \frac{AB}{AC}(**)

    Từ (*) và (**) \Rightarrow \frac{BD}{DC} = \frac{EB}{EC} \Rightarrow \frac{CE}{BE} = \frac{CD}{BD}

  • Câu 15: Thông hiểu
    Tính độ dài cạnh MP

    Cho tứ giác ACBD có AB vuông góc với CD. Gọi M, N, P, Q lần lượt là trung điểm của BC, BD, AD, AC. Biết BC // AD, BC = 4cm, AD = 16cm. Tính độ dài cạnh MP.

    Hướng dẫn:

    Hình vẽ minh họa

    Trong tam giác ACD, PQ là đường trung bình, suy ra PQ // CD.

    Tương tự MN // CD, MQ // AB, NP // AB.

    Từ đó ta có MN // PQ và NP // MQ

    Suy ra MNPQ là hình bình hành. Mặt khác AB ⊥ CD; MN ⊥ MQ.

    Vậy MNPQ là hình chữ nhật.

    Ta có MP = NQ.

    Theo giả thiết thì BCAD là hình thang với hai đáy BC, AD và QN là đường trung bình nên MP = NQ = 1/2.(BC + AD) = 10cm.

0/15
15 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (40%):
    2/3
  • Thông hiểu (47%):
    2/3
  • Vận dụng (13%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 20 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 8 CTST

Đăng nhập