Cho ΔABC có I, K lần lượt là trung điểm của AB và AC. Biết BC = 10cm. Khi đó:
Hình vẽ minh họa
Ta có:
=> là đường trung bình tam giác ABC
Cho 
đều cạnh , gọi là trung điểm của và . Tính chu vi của tứ giác bằng
Hình vẽ minh họa
Ta có: M, N là trung điểm của các cạnh AB và AC
=> MN là đường trung bình của tam giác ABC
Do tam giác ABC đều nên ta có:
Chu vi tứ giác MNCB là:
Cho tam giác . Trên tia đối của tia AB lấy điểm D sao cho , trên tia đối của tia BC lấy điểm E sao cho . Gọi I là giao điểm của AC và DE. Mối liên hệ giữa DI và DE là:
Hình vẽ minh họa
Qua điểm B kẻ đường thẳng BJ // CI cắt ED tại J và BC = BE
Khi đó BJ là đường trung bình tam giác CIE
và J là trung điểm của IE
Ta có AI // BJ và AB = AB
Khi đó AI là đường trung bình tam giác DBJ
=> I là trung điểm của cạnh DJ
Suy ra
Cho góc . Cho một điểm A cố định trên tia Ox sao cho , một điểm B bất kì trên tia Oy. Trên tia đối của tia BA lấy điểm C sao cho . Hỏi khi điểm B di động trên tia Oy thì điểm C di động trên đường nào?
Hình vẽ minh họa
Gọi M là trung điểm của BC.
Vẽ A và
Xét tam giác AOH vuông tại H có nên
Xét tam giác BCE, dễ thấy MD là đường trung bình nên
Điểm C cách Oy một khoảng là 2cm nên C di động trên đường thẳng song song với Oy và cách Oy một khoảng bằng 2cm.
Cho hình vuông ABCD, hai đường chéo cắt nhau tại O. Gọi M và N lần lượt là trung điểm của OA và CD. Khẳng định nào dưới đây đúng nhất?
Hình vẽ minh họa
Gọi E là trung điểm của OB thì ME là đường trung bình của tam giác AOB
=>
Do đó .
Tứ giác MECN là hình bình hành
Ta có: tại F (vì
),
(tính chất đường chéo hình vuông).
Xét tam giác có E là trực tâm nên
do đó
Xét tam giác và tam giác
có:
(một nửa của hai đoạn thẳng bằng nhau).
Vậy
Từ (1) và (2) suy ra tam giác MNB vuông cân.
Cho hình thoi ABCD có . Gọi O là giao điểm của hai đường chéo. Đường cao kẻ từ O đến mỗi cạnh của hình thoi bằng 10cm. Xác định độ dài cạnh hình thoi.
Hình vẽ minh họa
Vẽ thì
và OH là đường trung bình của tam giác BKD
Xét tam giác ABK vuông tại K có
Từ (*) và (**) suy ra
Cho tam giác ABC có chu vi . Gọi là trung điểm của các cạnh . Chu vi của tam giác EFP là:
Hình vẽ minh họa
Chu vi tam giác ABC là:
Ta có: E, F là trung điểm của các cạnh AB và BC
=> EF là đường trung bình của tam giác ABC
Ta có: F, P là trung điểm của BC và AC
=> FP là đường trung bình của tam giác ABC
Lại có: E, P là trung điểm của AB và AC
=> EP là đường trung bình của tam giác ABC
Chu vi tam giác EFP là:
Cho hình thang , . Kẻ , gọi K là trung điểm của HC. Tính số đo góc .
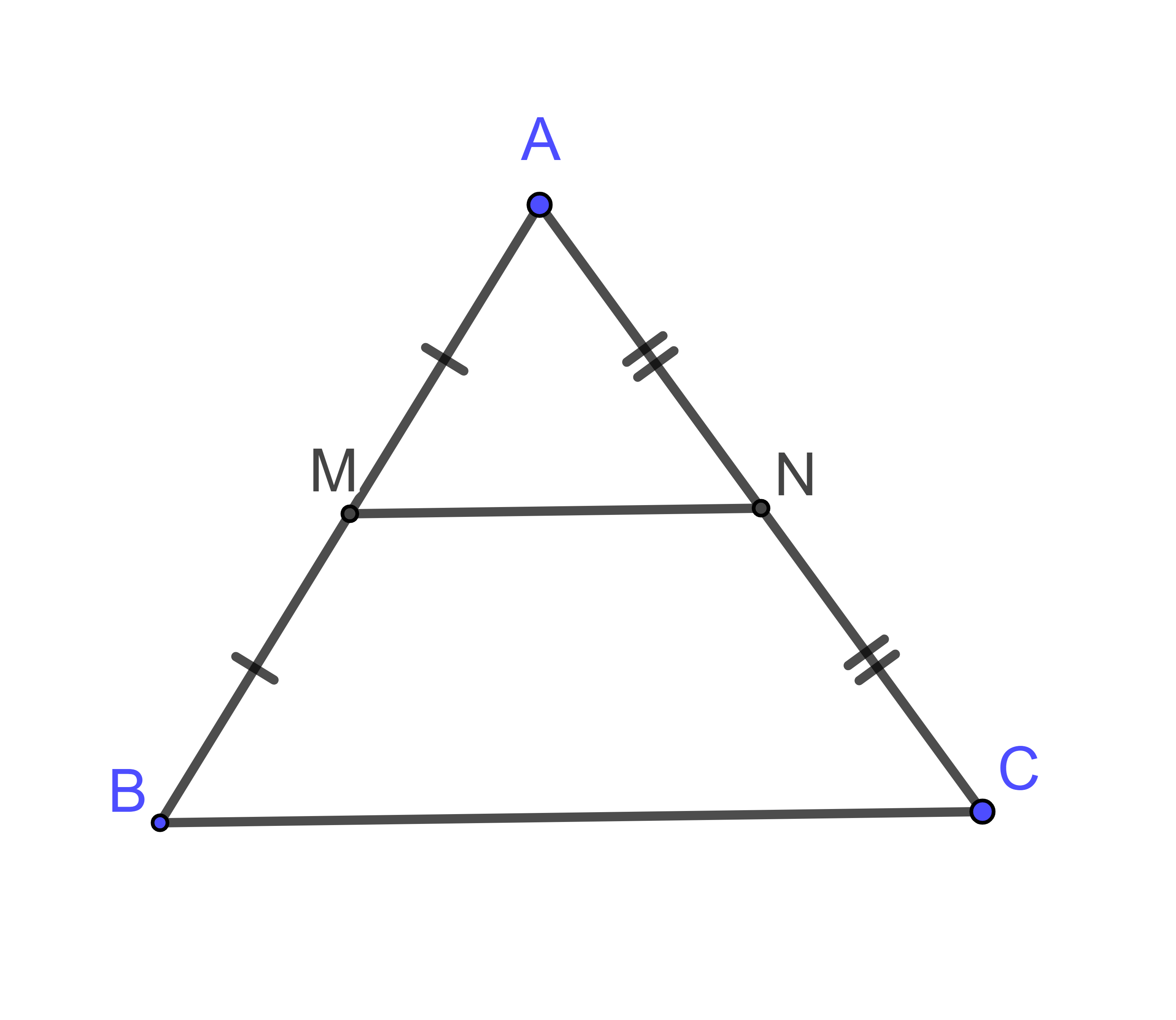
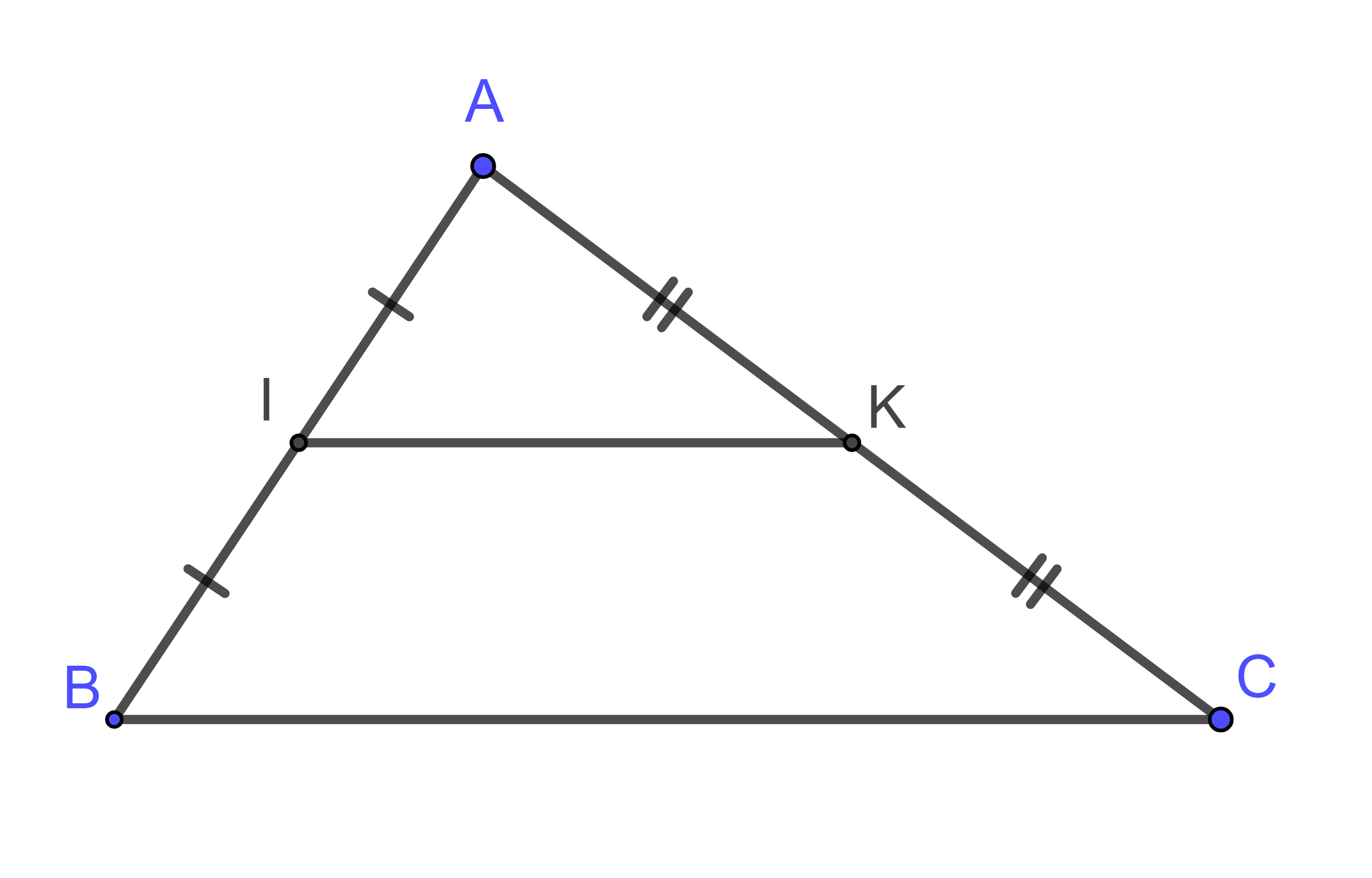
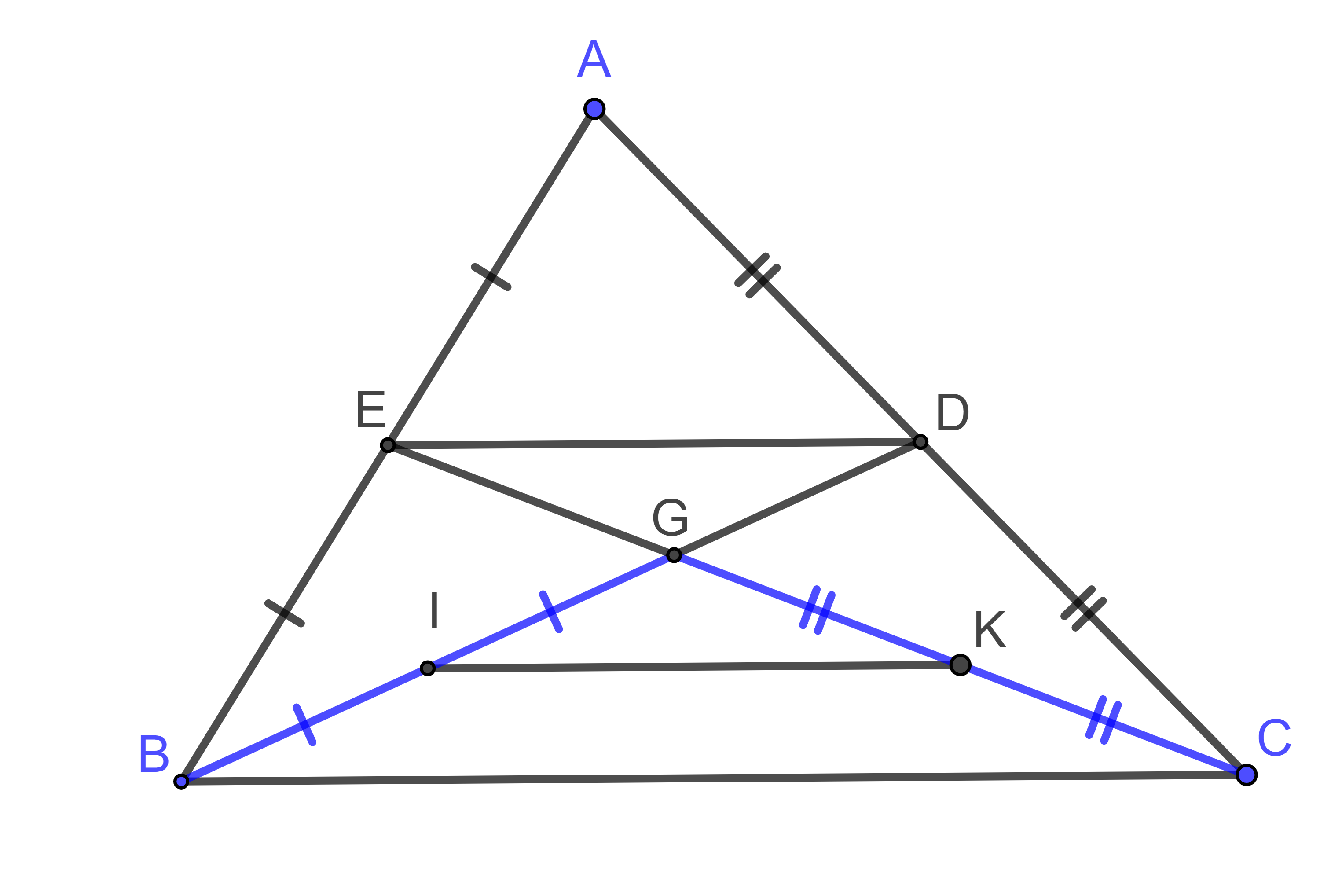
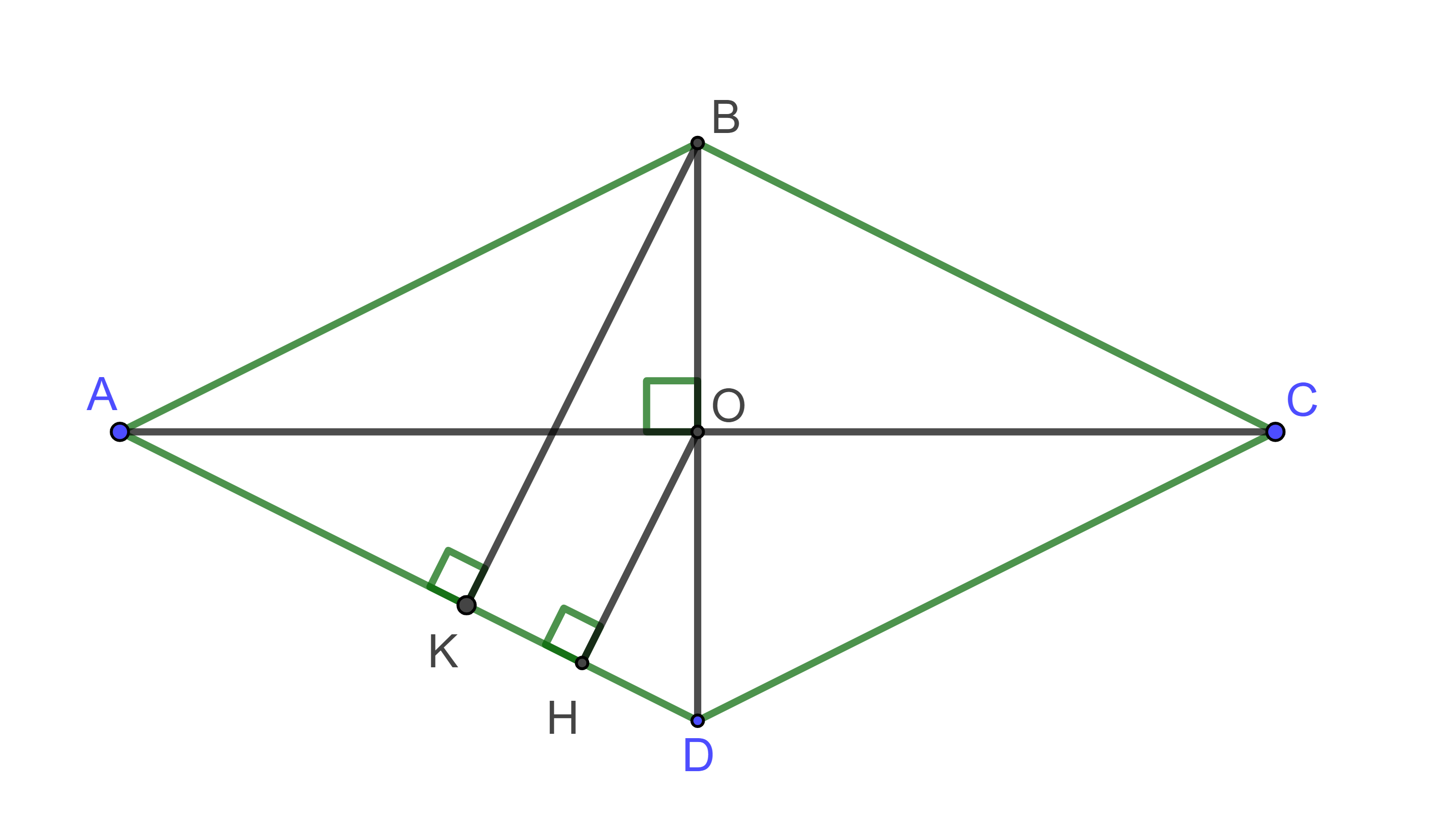
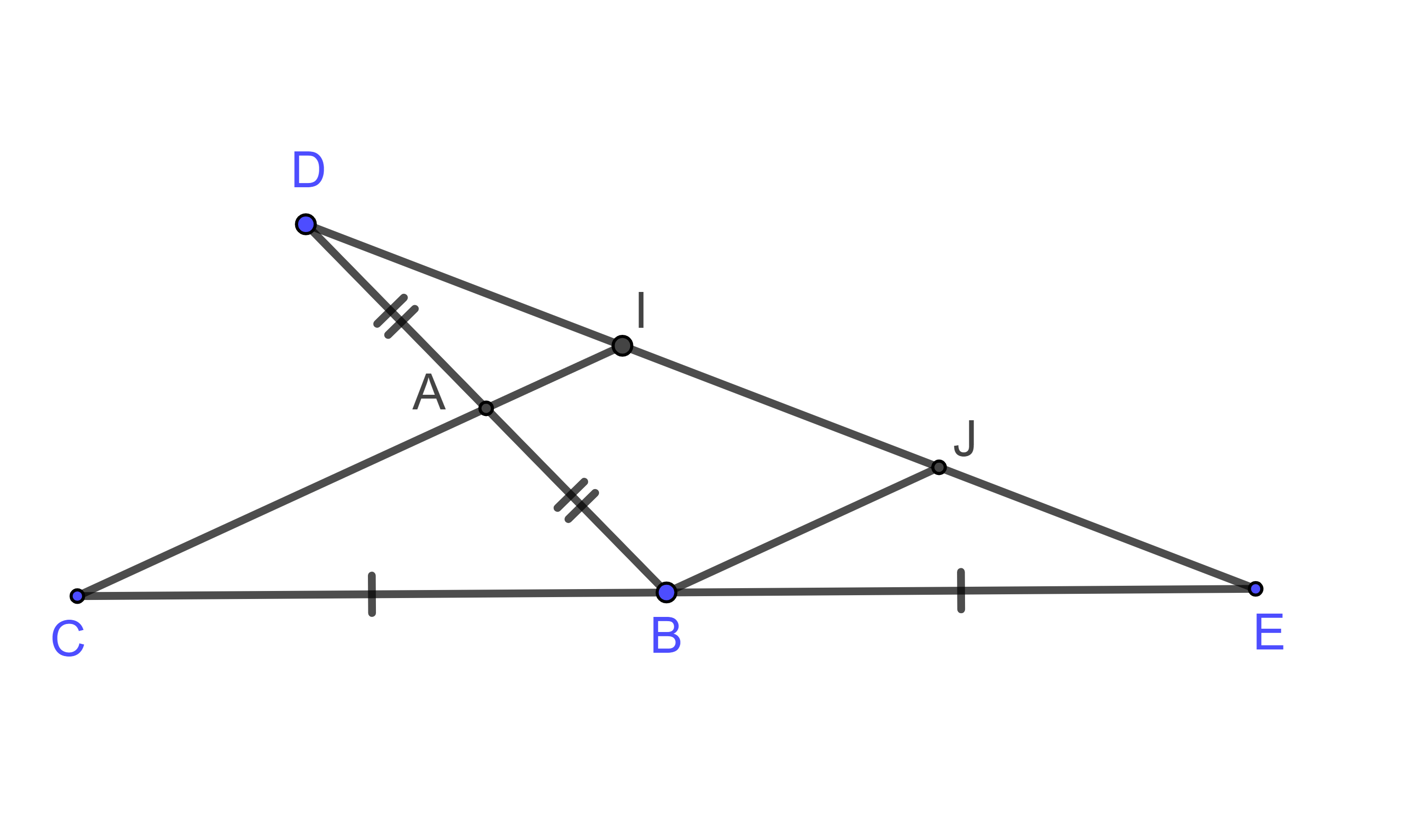
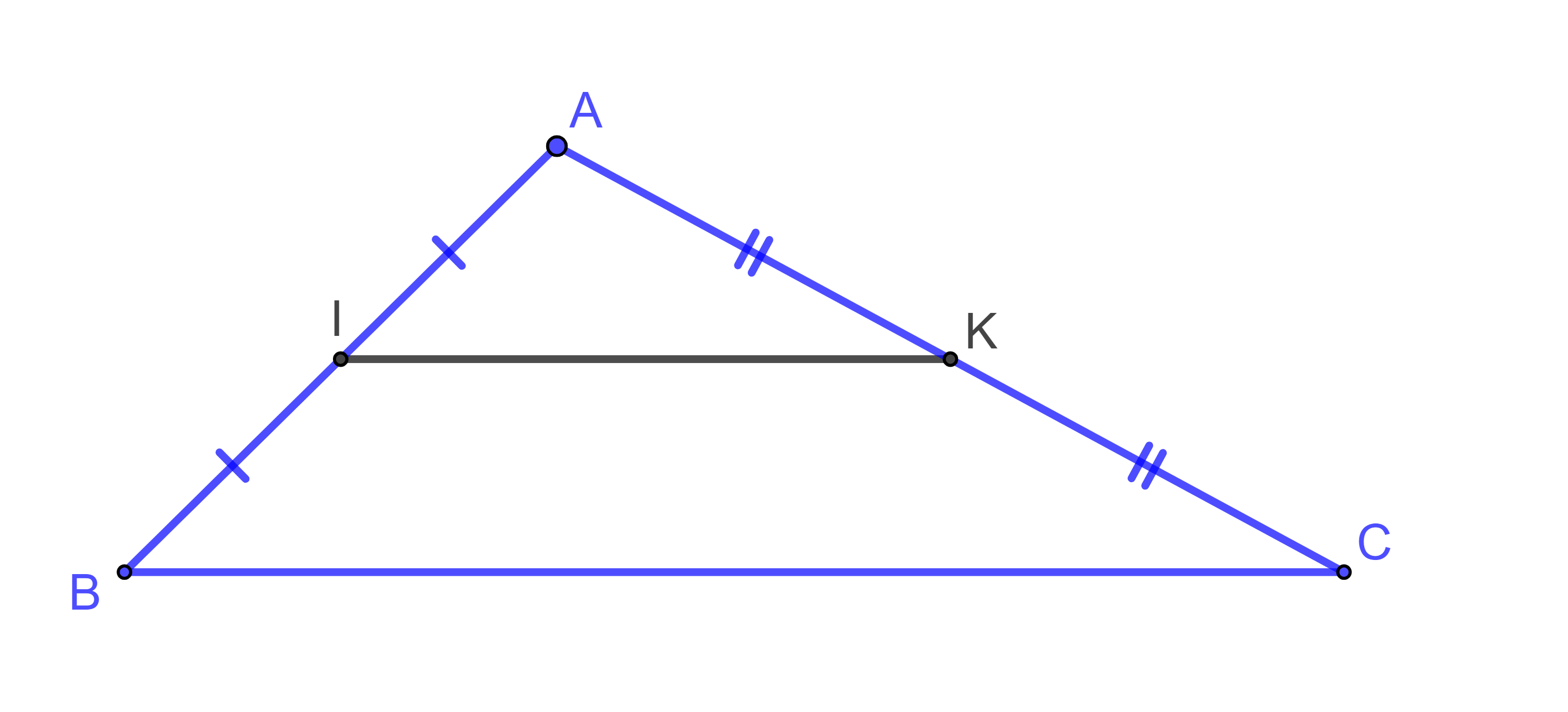
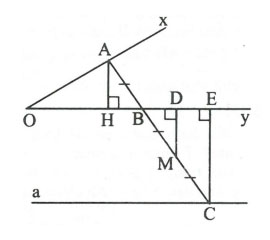
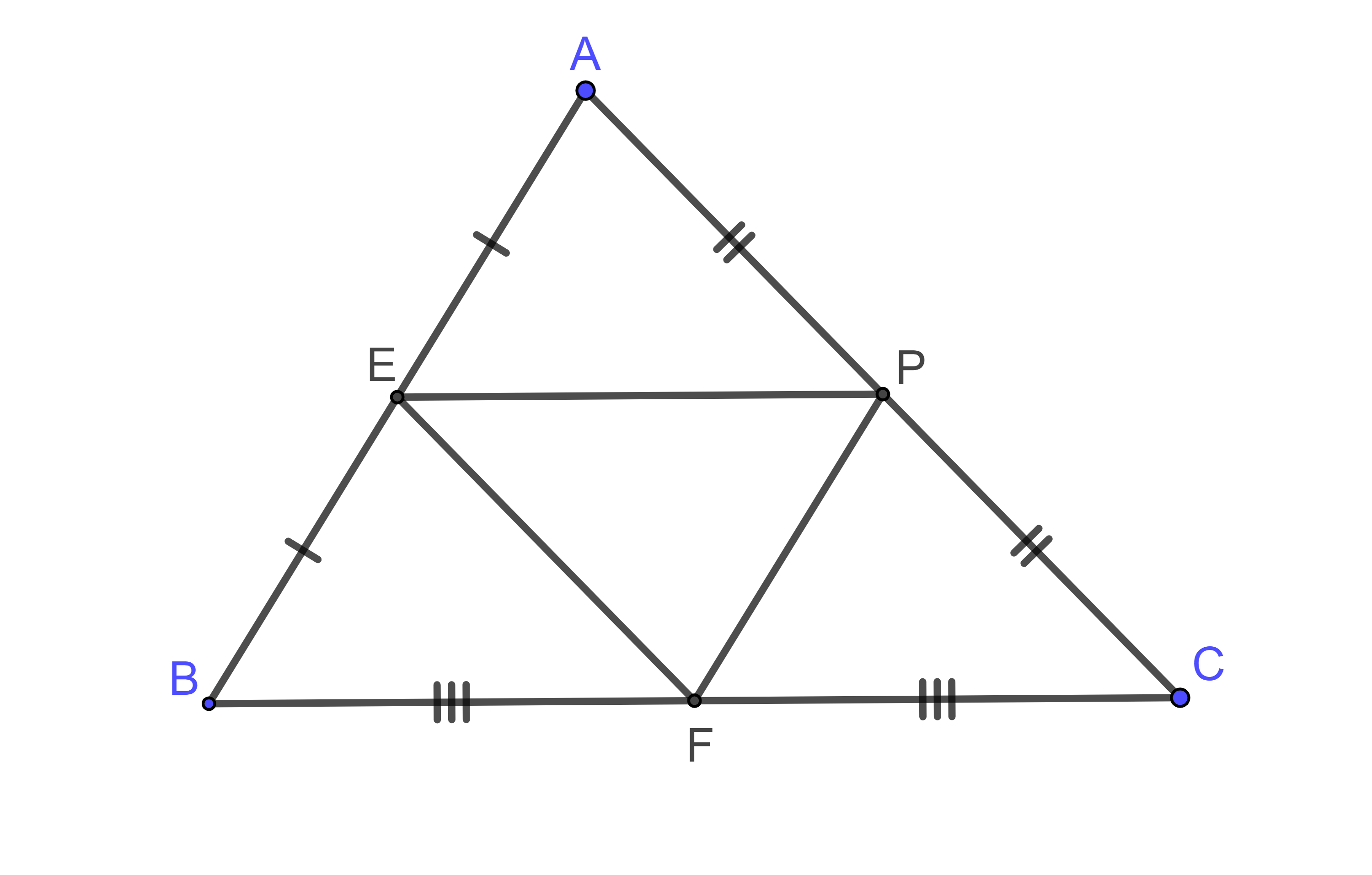
Hình vẽ minh họa
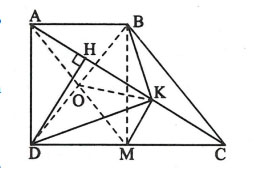
Gọi M là trung điểm của CD.
Xét tam giác có
là đường trung bình nên
do đó
(vì
).
Tứ giác có
và
nên
là hình bình hành.
Hình bình hành này có góc nên là hình chữ nhật. Suy ra
và
Xét tam giác AKM vuông tại K có KO là đường trung tuyến nên
Xét tam giác KBD có KO là đường trung tuyến mà
Suy ra tam giác KBD vuông tại K
=>
Cho tam giác ABC có I, K lần lượt là trung điểm của AB và AC. Biết . Ta có:
Ta có:
I, K là trung điểm của AB và AC
=> IK là đường trung bình tam giác ABC
Cho tam giác ABC đều cạnh 2cm. Gọi trung điểm của AB và AC lần lượt tại M và N. Chu vi của tứ giác MNCB bằng:
Hình vẽ minh họa
Ta có: M, N là trung điểm của các cạnh AB và AC
=> MN là đường trung bình của tam giác ABC
Do tam giác ABC đều nên ta có:
Chu vi tứ giác MNCB là:
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Trong các câu sau câu nào đúng?
Hình vẽ minh họa:
Xét tam giác ABC, ta có:
(Vì E là trung điểm của A)
(Vi D là trung điểm của AC)
=> ED là đường trung bình của ΔABC
(tính chất đường trung bình của tam giác) (*)
Xét tam giác GBC, ta có:
(Vì I là trung điểm của BG)
(Vì K là trung điểm của CG)
=> IK là đường trung bình của ∆GBC
(tính chất đường trung bình của tam giác) (**)
Từ (*) và (**) suy ra: .
Chọn khẳng định đúng
Đáp án đúng: "Đường trung bình của tam giác là đoạn nối trung điểm hai cạnh của tam giác."
Cho tam giác , các đường trung tuyến và cắt nhau ở G. Gọi theo thứ tự là trung điểm của . Tính biết .
Hình vẽ minh họa
Xét tam giác ABG có:
=> EI là đường trung bình của tam giác ABG
Xét tam giác AGC có:
=> DK là đường trung bình của tam giác AGC
Cho tam giác, đường phân giác BM. Từ M vẽ một đường thẳng vuông góc với BM cắt đường thẳng BC tại D. Tìm mối liên hệ giữa hai đoạn thẳng BD và CM.
Hình vẽ minh họa
Gọi E là giao điểm của đường thẳng DM và AB.
Tam giác DBE có BM vừa là đường phân giác vừa là đường cao nên là tam giác cân
Do đó
Gọi N là trung điểm của BE thì MN là đường trung bình của tam giác EBD
=> Tam giác NBM cân
Tứ giác BCMN là hình thang cân
Xét tam giác MBE vuông tại M có MN là đường trung tuyến nên
Cho có lần lượt là trung điểm của và . Biết . Ta có:
Hình vẽ minh họa
Ta có: I và K lần lượt là trung điểm của AB và AC
Suy ra IK là đường trung bình của tam giác ABC
