Luyện tập Hình chóp tam giác đều - Hình chóp tứ giác đều

Hình chóp tứ giác đều có các cạnh bên bằng nhau và các cạnh đáy bằng nhau nên mặt bên là những tam giác cân.

Hình chóp tứ giác đều có 5 mặt.

Ta có: S.ABC là hình chóp tứ giác đều có các mặt là tam giác đều.

Mặt khác

=> M là trung điểm của AB

Và O là trọng tâm giác tam giác ABC

Suy ra

Đặt AB = BC = x, áp dụng định lí Pi – ta – go cho tam giác BCM

Vậy AB = 4

Hình vẽ minh họa

Gọi H là trung điểm AB, ta có SH là trung đoạn của hình chóp

Trong tam giác SBH vuông tại H, theo Pi – ta – go ta có:

Vậy độ dài trung đoạn là .

Hình có thể ghép thành hình chóp tứ giác đều là:

Hình chóp tứ giác đều có các cạnh bên bằng nhau và các cạnh đáy bằng nhau nên mặt bên là những tam giác cân.

Mỗi mặt bên của hình chóp tứ giác đều là: tam giác cân.

Ta có A.BCDE là hình chóp tứ giác đều

=> BCDE là hình vuông

=> CD = DE = 48cm

F là trung điểm của DE => DF = FE = 48/2 = 24cm

Tam giác ADE là tam giác cân, F là trung điểm của DE

=> FA là đường cao của tam giác ADE

Áp dụng định lí Py – ta – go cho tam giác AFE vuông tại F ta được:

Hình chóp tam giác đều có 6 cạnh.

Hình chóp đều là hình chóp có mặt đáy là đa giác đều và các mặt bên là các tam giác cân có chung đỉnh.

Hình vẽ minh họa

Ta có: ABCD là hình vuông và các cạnh bên bằng nhau

Ta có:

Trong tam giác SOA vuông tại O theo Pi – ta – go ta có:

Vậy chiều cao hình chóp là cm.

Hình vẽ minh họa

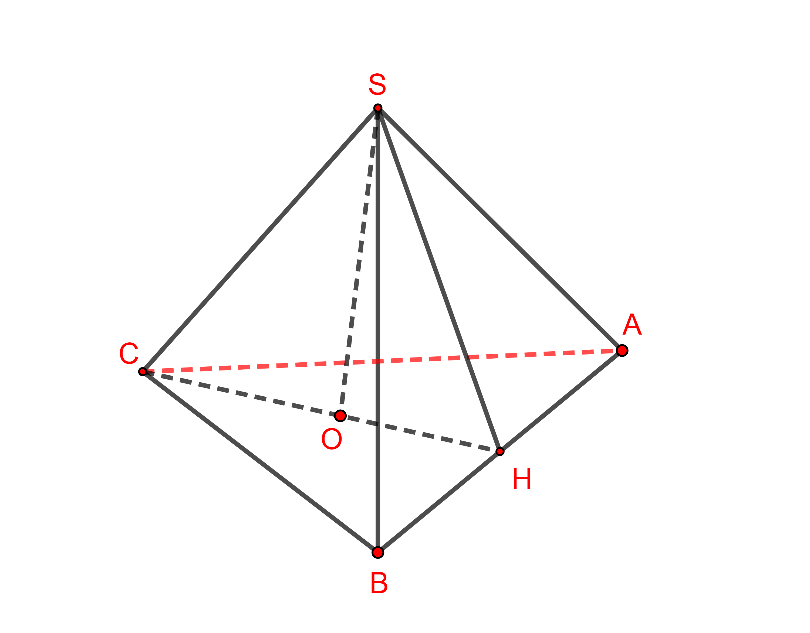
Hình chóp tam giác đều S ABC nên ABC là tam giác đều.

Gọi H là trung điểm AB, O là trong tâm tam giác ABC

Ta có CH là đường cao tam giác ABC Trong tam giác CHB vuông tại H ta có:

Trong tam giác vuông SOC vuông tại O ta có:

Vậy chiều cao hình chóp là: .