Cho hình thang cân ![]() có
có ![]() . Khi đó các góc B của hình thang cân là:
. Khi đó các góc B của hình thang cân là:
Hình vẽ minh họa
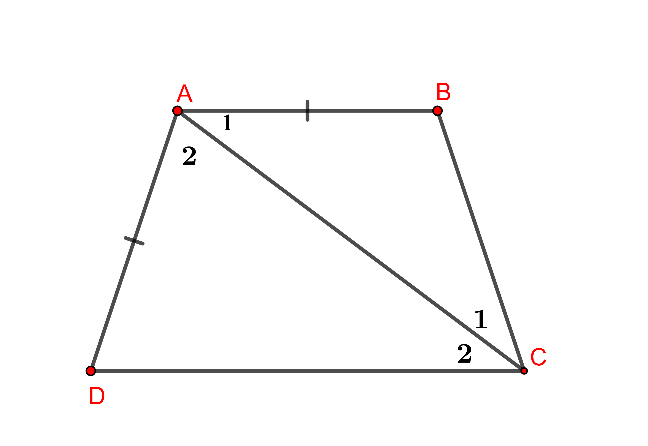
Ta có tam giác ABC cân tại B =>
Tương tự ta chứng minh được:
Có
Cho hình thang cân ![]() có
có ![]() . Khi đó các góc B của hình thang cân là:
. Khi đó các góc B của hình thang cân là:
Hình vẽ minh họa

Ta có tam giác ABC cân tại B =>
Tương tự ta chứng minh được:
Có
Hình thang ABCD có AB // CD và ![]() . Tính số đo góc B và góc C.
. Tính số đo góc B và góc C.
Ta có ABCD là hình thang:
Ta có:
Ta lại có:
Câu nào sau đây là đúng khi nói về hình thang:
Câu đúng: “Hình thang là tứ giác có hai cạnh đối song song.”
Cho hình vẽ sau:

Tìm ![]() biết
biết ![]() là hình thang với
là hình thang với ![]()
Ta có:
Cho hình thang ABCD như hình vẽ:

Tính độ dài cạnh AB.
Vẽ ta được:
Xét vuông tại
có:
Xét vuông tại
có:
Vậy
Góc kề cạnh bên của hình thang có số đo là ![]() . Góc kề còn lại của cạnh bên đó là:
. Góc kề còn lại của cạnh bên đó là:
Vì tổng hai góc kề cạnh bên của hình thang bằng nên góc kề còn lại của cạnh bên đó có số đo bằng
Cho hình thang cân ![]() như hình vẽ:
như hình vẽ:

Tính độ dài AB.
Hình vẽ minh họa
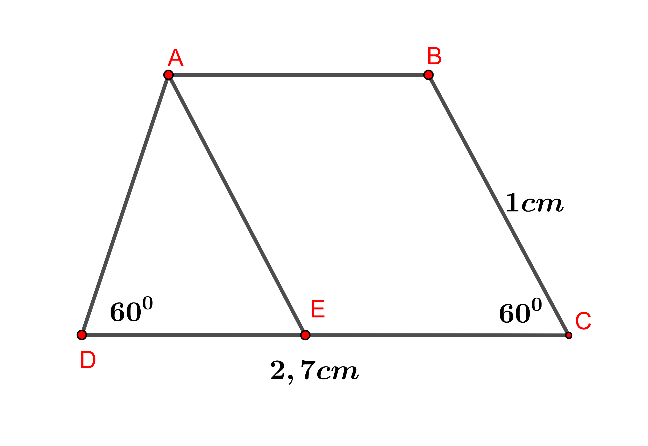
Kẻ
suy ra tam giác
đều
Chọn đáp án sai.
Đáp án sai: “Hình thang cân là hình có hai cạnh bằng nhau."
Cho hình thang ![]() có
có ![]() . Xác định số đo các góc B và C. Biết
. Xác định số đo các góc B và C. Biết ![]() .
.
Hình vẽ minh họa
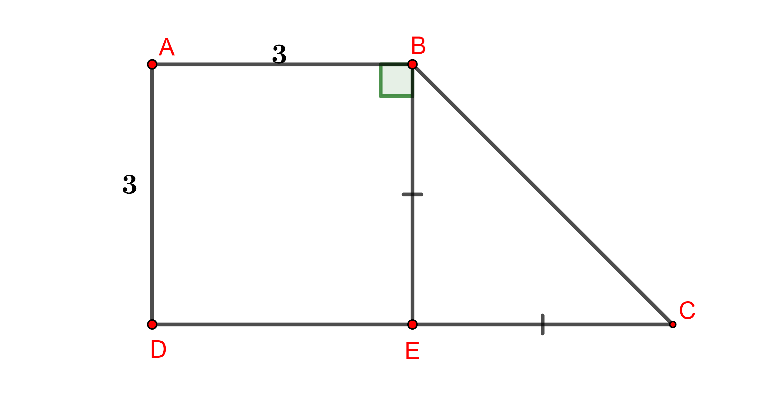
Kẻ thì
do cùng vuông góc với CD nên hình thang
có hai cạnh bên song song
Áp dụng nhận xét về hình thang có hai cạnh bên song song vào hình thang và giả thiết ta được
Suy ra vuông cân tại E nên
Ta lại có:
Cho hình thang cân ![]() có
có ![]() ,
, ![]() ,
, ![]() là tia phân giác của góc
là tia phân giác của góc ![]() . Tính độ dài cạnh
. Tính độ dài cạnh ![]() của hình thang biết chu vi hình thang bằng
của hình thang biết chu vi hình thang bằng ![]() .
.
Hình vẽ minh họa
Gọi => Tam giác
đều.
;
Có là tia phân giác của góc
=>
=> Tam giác cân tại
Chu vi hình thang là
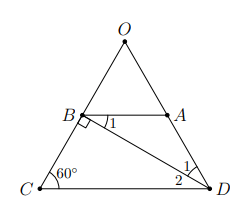
Cho tam giác đều ![]() . Từ một điểm
. Từ một điểm ![]() nằm bên trong tam giác ta vẽ các tia gốc
nằm bên trong tam giác ta vẽ các tia gốc ![]() song song với
song song với ![]() cắt
cắt ![]() ở
ở ![]() , song song với
, song song với ![]() cắt
cắt ![]() tại
tại ![]() , song song với
, song song với ![]() cắt
cắt ![]() tại
tại ![]() . Gọi chu vi tam giác
. Gọi chu vi tam giác ![]() là
là ![]() . Chọn khẳng định đúng.
. Chọn khẳng định đúng.
Ta có:
Chu vi tam giác là:
Khoảng cách từ đến 3 đỉnh là:
Ta có hình thang là hình thang cân
Chứng minh tương tự ta có:
Cho hình thang ABCD có ![]() . Tính độ dài cạnh
. Tính độ dài cạnh ![]() biết
biết ![]() .
.
Hình vẽ minh họa
Tam giác vuông tại
, theo định lí Pythagore ta có:
Kẻ . Hình thang
có
nên:
Tam giác vuông tại
, theo định lí Pythagore ta có:
Cho hình thang ![]() ,
, ![]() có đường chéo AC và BD vuông góc với nhau tại
có đường chéo AC và BD vuông góc với nhau tại ![]() . Trên đáy AD lấy M sao cho AM bằng độ dài đường trung bình của hình thang. Chọn khẳng định đúng.
. Trên đáy AD lấy M sao cho AM bằng độ dài đường trung bình của hình thang. Chọn khẳng định đúng.
Hình vẽ minh họa
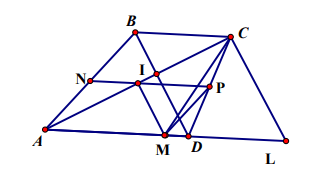
Gọi L là điểm đối xứng với đối xứng với A qua M
Gọi NM là đường trung bình của hình thang như hình vẽ
Gọi I là giáo điểm của AC và NP
Vì =>
mà N là trung điểm AB
=> I cũng là trung điểm AC (1)
Suy ra
Xét hình thang ABCD ta có:
Suy ra mà
Suy ra tứ giác BCLD là hình bình hành
Suy ra
Mà (gt)
=> (3)
Từ (1), (2) và (3) suy ra và MI là đường trung trục của đoạn thẳng AC
Suy ra
Vậy tam giác MAC cân tại M.
