Tứ giác có hai cạnh đối song song và hai đường chéo bằng nhau là:
Tứ giác có hai cạnh đối song song và hai đường chéo bằng nhau là hình thang cân.
Tứ giác có hai cạnh đối song song và hai đường chéo bằng nhau là:
Tứ giác có hai cạnh đối song song và hai đường chéo bằng nhau là hình thang cân.
Cho hình vuông ![]() có cạnh bằng
có cạnh bằng ![]() . Giả sử
. Giả sử ![]() là hai điểm lần lượt nằm trên cạnh
là hai điểm lần lượt nằm trên cạnh ![]() sao cho
sao cho ![]() . Tính chu vi tam giác
. Tính chu vi tam giác ![]() ?
?
Hình vẽ minh họa:
Đường thẳng qua C vuông góc với CE cắt AD tại I
(cùng phụ với góc
)
Do đó hai tam giác vuông BCE và DCI bằng nhau
Suy ra
Từ đó ta chứng minh được
=> .
Từ đây, tương tự như trên ta chứng minh được tam giác AEF có chu vi bằng 2.
Cho tam giác ![]() cân tại
cân tại ![]() , trung tuyến
, trung tuyến ![]() . Gọi
. Gọi ![]() là trung điểm của
là trung điểm của ![]() ,
, ![]() là điểm đối xứng với
là điểm đối xứng với ![]() qua
qua ![]() . Tứ giác
. Tứ giác ![]() là hình gì?
là hình gì?
Hình vẽ minh họa
Tam giác cân tại
,
là đường trung tuyến nên
đồng thời là đường cao.
Xét tứ giác có:
Suy ra tứ giác là hình bình hành
Lại có (cmt) nên hình bình hành
là hình chữ nhật.
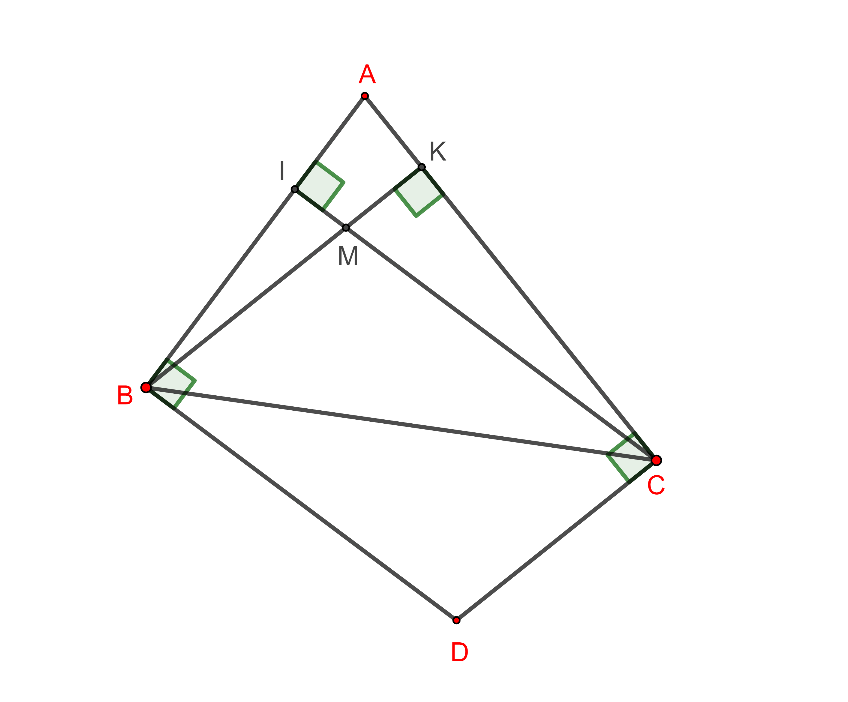
Cho ![]() nhọn, các đường cao
nhọn, các đường cao ![]() . Tia phân giác của góc ABD và ACE cắt nhau tại O, cắt AC và AB lần lượt tại N và M. Tia BN cắt CE tại K, tia CM cắt BD tại H. Khi đó tứ giác MNHK là hình gì?
. Tia phân giác của góc ABD và ACE cắt nhau tại O, cắt AC và AB lần lượt tại N và M. Tia BN cắt CE tại K, tia CM cắt BD tại H. Khi đó tứ giác MNHK là hình gì?
Hình vẽ minh họa:
Ta có:
Xét tam giác ABN có (góc ngoài của tam giác) (2)
Từ (1) và (2) suy ra
Lại có CO là phân giác góc NCK từ đó ta có O là trung điểm NK.
Chứng minh tương tự, O là trung điểm của MH.
Tứ giác MNHK có hai đường chéo vuông góc nhau tại trung điểm mỗi đường nên MNHK là hình thoi.
Cho hình thang cân ![]() có đường chéo BD vuông góc với cạnh bên BC và đồng thời BD là tia phân giác góc
có đường chéo BD vuông góc với cạnh bên BC và đồng thời BD là tia phân giác góc ![]() . Tính số đo các góc B và góc D hình thang cân ABCD.
. Tính số đo các góc B và góc D hình thang cân ABCD.
Tam giác DBC vuông:
Cho hình thang ![]() biết
biết ![]() . Tính đường cao
. Tính đường cao ![]() .
.
Hình vẽ minh họa
Ta tính được
Vận dụng nhận xét hình thang có hai cạnh bên song song thì hai cạnh đáy bằng nhau, để tính được
Chứng minh tam giác vuông cân tại
, nên
.
Một tứ giác là hình bình hành nếu nó là:
Hình bình hành là tứ giác có hai cạnh đối bằng nhau và song song.
Cho hình vẽ.

Tính độ dài cạnh DC. biết ![]() .
.
Tam giác vuông tại
nên
Lại có BD là phân giác góc nên
Tam giác ABC vuông tại A có nên
Áp dụng định lí Pythagore cho tam giác ABC vuông tại A ta có
Trong tam giác vuông ABC vuông tại A có: nên
Áp dụng định lí Pythagore cho tam giác ABD vuông tại A ta có
Tính giá trị của x trong hình vẽ dưới đây:

Kẻ
Khi đó ACDH là hình chữ nhật, suy ra:
Do đó:
Áp dụng định lí Pythagore cho tam giác ∆AHB vuông tại H, ta có:
Hình thoi có độ dài hai đường chéo lần lượt bằng ![]() và
và ![]() . Độ dài cạnh hình thoi đó là:
. Độ dài cạnh hình thoi đó là:
Hình vẽ minh họa
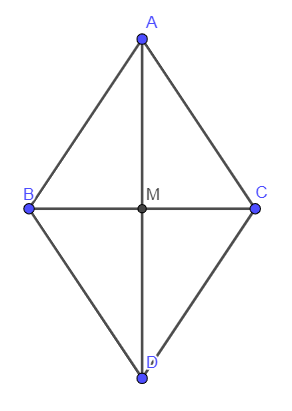
Ta có:
Gọi là giao điểm của
Do là hình thoi suy ra
Áp dụng định lí Pythagore cho tam giác vuông tại
ta có:
Vậy độ dài cạnh hình thoi là .
Hình bình hành có hai đường chéo vuông góc là:
Hình bình hành có hai đường chéo vuông góc là hình thoi.
Chọn đáp án không chính xác trong các đáp án dưới đây?
Ta có:
Trong hình vuông có hai đường chéo vuông góc với nhau, bằng nhau và cắt nhau tại trung điểm mỗi đường
Hai đường chéo trong hình vuông đồng thời là trục đối xứng của hình vuông đó.
Vậy đáp án không chính xác là: “Trong hình vuông có hai đường chéo không vuông góc với nhau.”
Cho hình thoi ![]() có
có ![]() . Kẻ
. Kẻ ![]() . Tính số đo góc
. Tính số đo góc ![]()
Hình vẽ minh họa
Hình thoi ABCD có AB = BC và nên tam giác ABC đều
Do đó đường cao AF cũng là đường phân giác suy ra
Tương tự ta cũng chứng minh được
Vậy
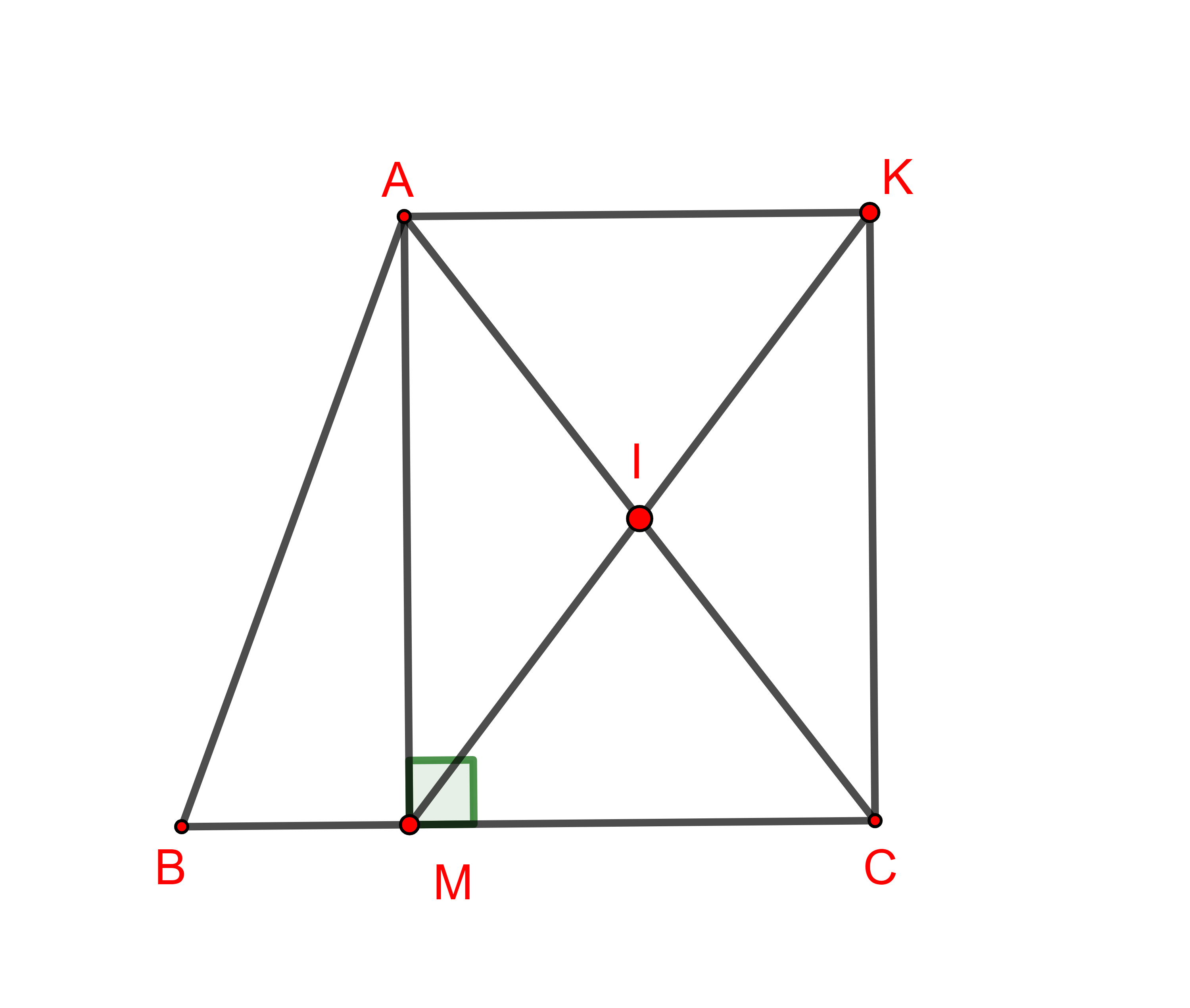
Cho tam giác ![]() có trực tâm
có trực tâm ![]() . Từ
. Từ ![]() và
và ![]() kẻ các đường vuông góc với
kẻ các đường vuông góc với ![]() và
và ![]() cắt nhau tại
cắt nhau tại ![]() . Xác định tứ giác
. Xác định tứ giác ![]() ?
?
Ta có:
Gọi là các đường cao của tam giác
.
Khi đó hay
(vì M là trực tâm).
Lại có (giả thiết) nên
(cùng vuông với
)
và (cùng vuông với
)
Suy ra tứ giác là hình bình hành.
Cho hình bình hành ABCD, ![]() . Gọi H là hình chiếu của B trên AD, M là trung điểm của CD. Tính số đo góc
. Gọi H là hình chiếu của B trên AD, M là trung điểm của CD. Tính số đo góc ![]() ?
?
Hình vẽ minh họa
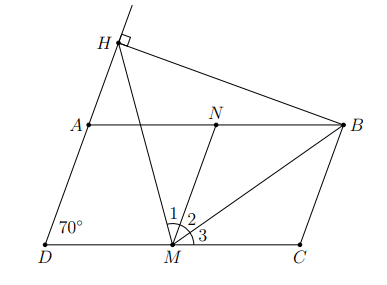
Gọi N là trung điểm AB, có
MN // DA
DA ⊥ BH
=> MN ⊥ BH và MN đi qua trung điểm của BH
=> MN là đường trung trực của BH
Lại có
