Lớp 8 Toán 8 - Cánh diều

Luyện tập Định lí Pythagore Cánh Diều

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 12 câu
  • Điểm số bài kiểm tra: 12 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Vận dụng
    Tìm độ dài cạnh huyền của tam giác

    Tính độ dài cạnh huyền của một tam giác vuông biết tỉ lệ cạnh góc vuông 3 : 4 và chu vi tam giác là 36cm.

    Hướng dẫn:

    Gọi độ dài hai cạnh góc vuông là x; y (cm) (y > x > 0)

    Và độ dài cạnh huyền là z(cm) (z > y)

    Theo bài ra ta có: \frac{x}{3} = \frac{y}{4}

    Khi đó: \frac{x}{3} = \frac{y}{4} = k;\left( {k > 0} ight) \Rightarrow \left\{ {\begin{array}{*{20}{c}} {x = 3k} \\ {y = 4k} \end{array}} ight.

    Áp dụng định lí Pythagore cho tam giác vuông ta có:

    x^{2} + y^{2} = z^{2} \Rightarrow z^{2} = (3k)^{2} + (4k)^{2} = 25k^{2}

    \Rightarrow z = 5k

    Suy ra x + y + z = 3k + 4k + 5k = 12k

    Mà x + y + z = 36

    \Rightarrow 12k = 36

    \Rightarrow k = 3

    Vậy x = 9cm;y = 12cm;z = 15cm

    Vậy độ dài cạnh huyền là 15cm.

  • Câu 2: Nhận biết
    Tính BC

    Cho tam giác ABC vuông tại A, biết AB = 4cm, BC = 5cm. Tính độ dài BC?

    Hướng dẫn:

    Áp dụng định lí Pythagore cho tam giác ABC vuông tại A ta có

    BC^{2} = AB^{2} + AC^{2}

    \Rightarrow BC^{2} - AB^{2} = AC^{2}

    \Rightarrow 5^{2} - 4^{2} = AC^{2}

    \Rightarrow AC^{2} = 9 \Rightarrow AC = 3cm

  • Câu 3: Thông hiểu
    Điền đáp án đúng vào chỗ trống

    Cho hình vẽ.

    Giá trị của x là: 24

    Đáp án là:

    Cho hình vẽ.

    Giá trị của x là: 24

    Quan sát hình vẽ ta thấy tam giác ABC vuông tại B.

    Áp dụng định lí Pythagore ta có:

    AC^{2} = AB^{2} + BC^{2}

    \Rightarrow BC^{2} = AC^{2} -AB^{2}

    \Rightarrow x^{2} = 26^{2} - 10^{2} =576

    \Rightarrow x = 24

    Vậy x = 24

  • Câu 4: Nhận biết
    Chọn khẳng định đúng

    Cho tam giác ABC vuông tại C, khi đó:

    Hướng dẫn:

    Vì tam giác ABC vuông tại B nên theo định lí Pythagore ta có: A{C^2} + B{C^2} = A{B^2}

    A{B^2} - B{C^2} = A{C^2}

  • Câu 5: Thông hiểu
    Chọn đáp án đúng

    Xác định dạng của tam giác ABC biết AB = 4cm;BC = 4\sqrt{2}cm;AC = 4cm?

    Hướng dẫn:

    Ta có: \left\{ \begin{gathered} A{B^2} + A{C^2} = {4^2} + {4^2} = 32 \hfill \\ AB = AC \hfill \\ B{C^2} = {\left( {4\sqrt 3 } ight)^2} = 32 \hfill \\ \end{gathered} ight.

    \Rightarrow \left\{ \begin{matrix} AB^{2} + AC^{2} = BC^{2} \\ AB = AC \\ \end{matrix} ight.

    Vậy tam giác ABC vuông cân tại A.

  • Câu 6: Nhận biết
    Chọn đáp án đúng

    Xác định tam giác vuông trong các tam giác có độ dài ba cạnh dưới đây.

    Hướng dẫn:

    Với bộ số 21dm;20dm;29dm ta thấy:

    \left\{ \begin{matrix} 21^{2} + 20^{2} = 841 \\ 29^{2} = 841 \\ \end{matrix} ight.\ \Rightarrow 21^{2} + 20^{2} = 29^{2}

    Vậy 21dm;20dm;29dm là ba cạnh của tam giác vuông.

  • Câu 7: Thông hiểu
    Tính độ lớn cạnh BC

    Cho tam giác ABC vuông cân tại A. Tính độ dài BC biết AB = AC = 4.

    Hướng dẫn:

    Tam giác ABC vuông cân tại A nên theo định lí Pythagore ta có:

    AB^{2} + AC^{2} = BC^{2} mà AB = AC = 4 nên BC^{2} = 4^{2} + 4^{2} = 32 \Rightarrow BC =\sqrt{32}

  • Câu 8: Vận dụng
    Tính độ dài cạnh DC

    Cho hình vẽ.

    Tính độ dài cạnh DC. biết AC = 3cm.

    Hướng dẫn:

    Tam giác ABC vuông tại A nên \widehat {ABC} + \widehat {ACB} = {90^0}

    \Rightarrow \widehat{ABC} = 90^{0} -\widehat{ACB} = 90^{0} - 30^{0} = 60^{0}

    Lại có BD là phân giác góc \widehat{ABC} nên \widehat{ABD} = \widehat{DBC} =\frac{\widehat{ABC}}{2} = \frac{60^{0}}{2} = 30^{0}

    Tam giác ABC vuông tại A có \widehat{ACB}= 30^{0} nên AB = \frac{1}{2}BC\Rightarrow BC = 2AB

    Áp dụng định lí Pythagore cho tam giác ABC vuông tại A ta có

    BC^{2} = AB^{2} + AC^{2}

    \Rightarrow (2AB)^{2} = AB^{2} +AC^{2}

    \Rightarrow 4AB^{2} = AB^{2} + 3^{2}\Rightarrow AB = \sqrt{3}

    Trong tam giác vuông ABC vuông tại A có: \widehat{ABD} = 30^{0} nên AD = \frac{1}{2}BD \Rightarrow BD =2AD

    Áp dụng định lí Pythagore cho tam giác ABD vuông tại A ta có

    BD^{2} = AD^{2} + AD^{2}

    \Rightarrow (2AD)^{2} = AB^{2} +AD^{2}

    \Rightarrow 4x^{2} = \left( \sqrt{3}ight)^{2} + x^{2}

    \Rightarrow x = 1

    => DC = 2cm

  • Câu 9: Thông hiểu
    Tìm x

    Tính giá trị của x trong hình vẽ dưới đây:

    Hướng dẫn:

    Kẻ AH\bot BD

    Khi đó ACDH là hình chữ nhật, suy ra: \left\{ \begin{matrix}HD = AC = 6cm \\AH = CD = 8cm \\\end{matrix} ight.

    Do đó: BH = BD - HD = 10 - 8 =2(cm)

    Áp dụng định lí Pythagore cho tam giác ∆AHB vuông tại H, ta có:

    AB^{2} = BH^{2} + AH^{2} = 2^{2} + 8^{2}= 68

    \Rightarrow AB =\sqrt{68}cm

  • Câu 10: Thông hiểu
    Tính độ dài cạnh AH

    Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H. Cho BH = 2cm; AB = 4cm. Tính độ dài cạnh AH.

    Hướng dẫn:

    Hình vẽ minh họa

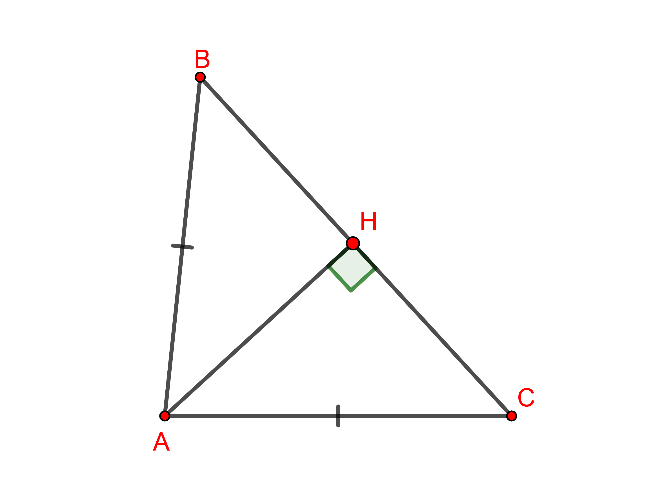
    Tính độ dài cạnh AH

    Ta có: Tam giác AHB vuông tại H, áp dụng định lí Pythagore ta được:

    AB^{2} = AH^{2} + BH^{2}

    \Rightarrow AH^{2} = AB^{2} - BH^{2}

    \Rightarrow AH^{2} = 4^{2} - 2^{2} = 12

    \Rightarrow AH = \sqrt{12}(cm)

    Vậy AH = \sqrt{12}cm

  • Câu 11: Vận dụng
    Tính độ dài các cạnh góc vuông

    Một tam giác vuông có cạnh huyền bằng 26cm độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông.

    Hướng dẫn:

    Áp dụng định lí Pythagore và tính chất của dãy tỉ số bằng nhau.

    Gọi độ dài hai cạnh góc vuông là x; y (x; y > 0)

    Theo định lí Pythagore ta có:

    x^{2} + y^{2} = 26^{2} \Rightarrow x^{2} + y^{2} = 676

    Theo đề bài ta có: \frac{x}{5} = \frac{y}{12} \Rightarrow \frac{x^{2}}{25} = \frac{y^{2}}{144} = \frac{x^{2} + y^{2}}{25 + 144} = \frac{676}{167} = 4

    \Rightarrow \left\{ \begin{matrix}\dfrac{x^{2}}{25} = 4 \\\dfrac{y^{2}}{144} = 4 \\\end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix}x^{2} = 100 \\y^{2} = 576 \\\end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix}x = 10 \\y = 24 \\\end{matrix} ight.

    Vậy hai cạnh góc vuông có độ dài lần lượt là 10cm;24cm

  • Câu 12: Nhận biết
    Tính độ dài AC

    Cho hình vuông ABCD cạnh bằng 2cm. Tính độ dài đường chéo AC.

    Hướng dẫn:

    Hình vẽ minh hoạ

    Theo bài ra ta có: ABCD là hình vuông nên AB = BC = 2cm

    Áp dụng định lí Pythagore cho tam giác ABC vuông tại B ta có:

    AC^{2} = AB^{2} + BC^{2} = 2^{2} + 2^{2}= 8

    \Rightarrow AC = \sqrt{8}cm

0/12
12 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (33%):
    2/3
  • Thông hiểu (42%):
    2/3
  • Vận dụng (25%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 23 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 8 CD

Đăng nhập