Cho hình thang ![]() . Gọi
. Gọi ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() . Gọi
. Gọi ![]() là giao điểm của đường thẳng qua
là giao điểm của đường thẳng qua ![]() vuông góc với
vuông góc với ![]() và đường thẳng qua
và đường thẳng qua ![]() vuông góc với
vuông góc với ![]() . Chọn khẳng định đúng?
. Chọn khẳng định đúng?
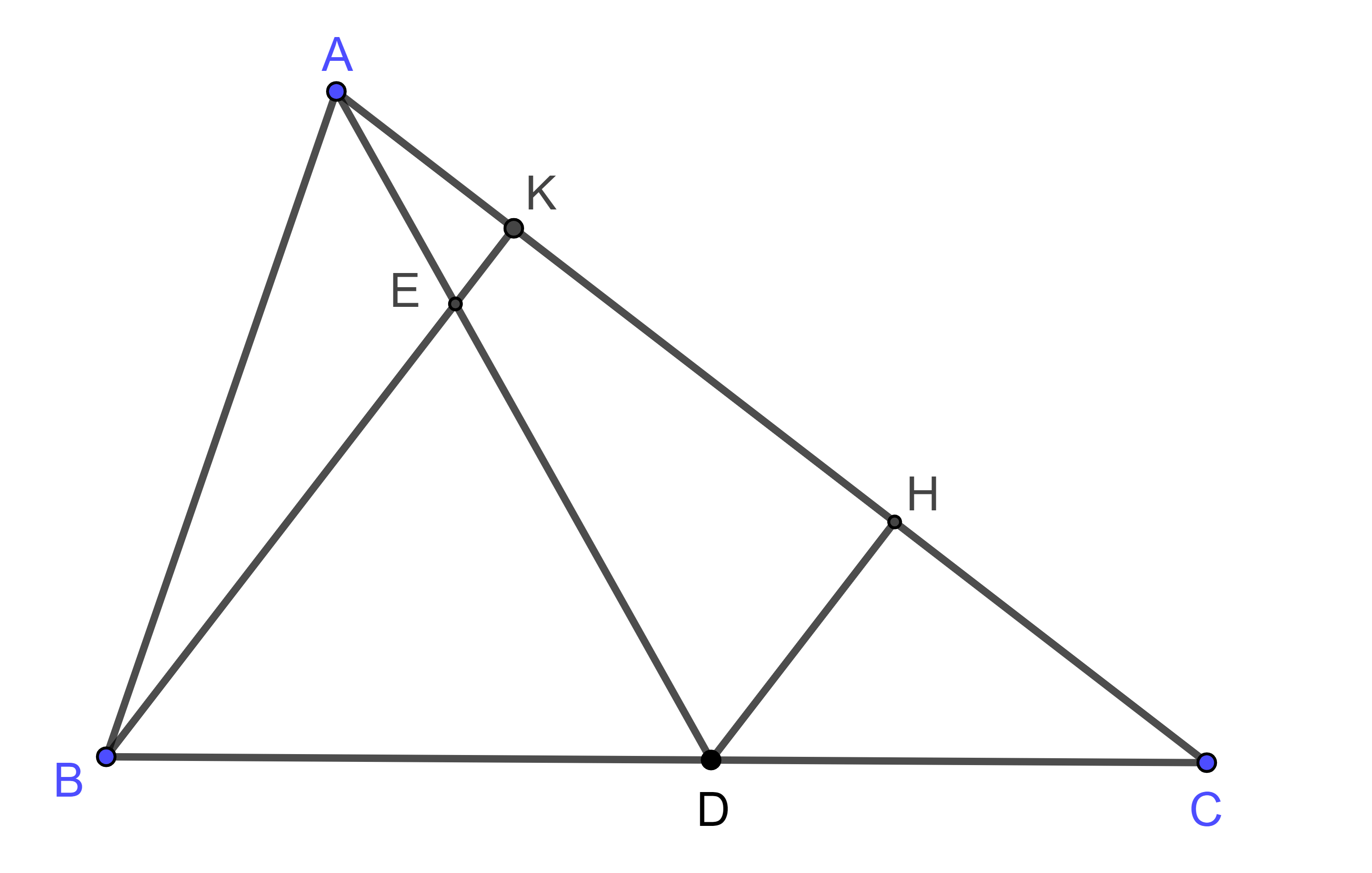
Hình vẽ minh họa
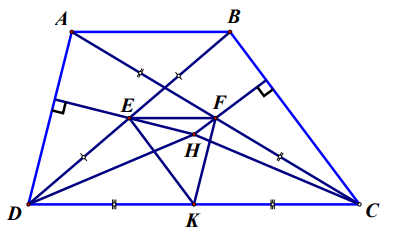
Ta có: lần lượt là trung điểm
=> là đường trung bình tam giác
=>
Mà =>
Ta có: lần lượt là trung điểm
=> là đường trung bình tam giác
Mà
=> H là trực tâm tam giác .