Luyện tập Hình vuông Cánh Diều

Nhận biết Thông hiểu Vận dụng

Bài kiểm tra này bao gồm 15 câu
Điểm số bài kiểm tra: 15 điểm
Xem lại kỹ lý thuyết trước khi làm bài
Chuẩn bị giấy và bút để nháp trước khi bắt đầu

Bắt đầu làm bài

00:00:00

Câu 1: Nhận biết
Chọn đáp án đúng
Chọn khẳng định đúng nhất trong các khẳng định dưới đây?
- A.
  Hình vuông là tứ giác có 4 góc vuông và 4 cạnh bằng nhau.
- B.
  Hình vuông là tứ giác có 4 cạnh bằng nhau.
- C.
  Hình vuông là tứ giác có 4 góc bằng nhau.
- D.
  Hình vuông là tứ giác có hai cạnh kề bằng nhau.
Hướng dẫn:
Ta có:

Tứ giác có 4 góc vuông là hình chữ nhật

Hình chữ nhật có 4 cạnh bằng nhau là hình vuông.

=> Hình vuông là tứ giác có 4 góc vuông và 4 cạnh bằng nhau.
Câu 2: Thông hiểu
Tính chu vi tam giác AEF
Cho hình vuông $ABCD$ có cạnh bằng $1$ . Giả sử $E;F$ là hai điểm lần lượt nằm trên cạnh $AB;AD$ sao cho $\widehat{ECF} = 45^{0}$ . Tính chu vi tam giác $AEF$ ?
- A.
  $8$
- B.
  $4$
- C.
  $2$
- D.
  $6$
Hướng dẫn:
Hình vẽ minh họa:
Đường thẳng qua C vuông góc với CE cắt AD tại I
$\widehat{ECF} = 45^{0} \Rightarrow\widehat{ICF} = \widehat{ECF} = 45^{0}$
$\widehat{BCE} = \widehat{DIC}$ (cùng phụ với góc $\widehat{ECD}$ )
$BC = DC$
Do đó hai tam giác vuông BCE và DCI bằng nhau
Suy ra $CE = CI$
Từ đó ta chứng minh được $\Delta ECF =\Delta ICF(c - g - c)$
=> $EF = FI$ .
Từ đây, tương tự như trên ta chứng minh được tam giác AEF có chu vi bằng 2.
Câu 3: Vận dụng
Xác định tam giác APQ
Cho tam giác $ABC$ . Phía ngoài tam giác $ABC$ dựng các hình vuông $BCDE, ACFG, ABKH$ rồi vẽ tiếp các hình bình hành $BEQK, CDPF$ . Xác định tam giác $APQ$ ?
- A.
  Tam giác vuông cân
- B.
  Tam giác vuông
- C.
  Tam giác đều
- D.
  Tam giác cân
Hướng dẫn:
Hình vẽ minh họa
Xét hai tam giác ABC và BQK
Ta có: $AB = BK; KQ = BE = AB$ ; $\widehat{BKQ} = \widehat{ABC}$ (cùng phụ với góc $\widehat{KBE}$ )
Suy ra $\Delta ABC = \Delta BKQ\Rightarrow \left\{ \begin{matrix}BQ = AC = AG \\\widehat{KBQ} = \widehat{CAB} \\\end{matrix} ight.$
$\Rightarrow \widehat{ABQ} =\widehat{BAG}$
Ta có $AQ = BG$ và $AQ // BG$
Chứng minh tương tự, $AHCP$ là hình bình hành, suy ra $AP = CH$ và $AP // CH$ .
Mặt khác, ta chứng minh được $\Delta ABG =\Delta AHC$ , từ đó suy ra $BG = CH$ và $BG ⊥ CH$ .
Do đó $AP = AQ$ và $AP ⊥ AQ$ suy ra tam giác APQ vuông cân tại A.
Câu 4: Thông hiểu
Tính bình phương đường chéo hình vuông
Cho hình vuông có chu vi $20 cm$ . Bình phương độ dài một đường chéo của hình vuông là:
- A.
  $32$
- B.
  $30$
- C.
  $25$
- D.
  $50$
Hướng dẫn:
Gọi hình vuông $ABCD$ có chu vi là $20cm$ .

Khi đó $4 . AB = 20cm$

$=> AB = 5cm = AB = CD = DA$

Xét tam giác ABC vuông tại B, theo định lý Pytago ta có

$AB^{2} + BC^{2} = AC^{2}$

$\Rightarrow 5^{2} + 5^{2} = AC^{2}$

$\Rightarrow AC^{2} = 50$
Câu 5: Nhận biết
Chọn khẳng định sai
Chọn đáp án không chính xác trong các đáp án dưới đây?
- A.
  Trong hình vuông có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
- B.
  Trong hình vuông có hai đường chéo không vuông góc với nhau.
- C.
  Trong hình vuông thì hai đường chéo đồng thời là hai trục đối xứng của hình vuông.
- D.
  Trong hình vuông có hai đường chéo vuông góc với nhau và bằng nhau.
Hướng dẫn:
Ta có:
Trong hình vuông có hai đường chéo vuông góc với nhau, bằng nhau và cắt nhau tại trung điểm mỗi đường
Hai đường chéo trong hình vuông đồng thời là trục đối xứng của hình vuông đó.
Vậy đáp án không chính xác là: “Trong hình vuông có hai đường chéo không vuông góc với nhau.”
Câu 6: Thông hiểu
Xác định tam giác DEF
Cho hình vuông $ABCD$ , lấy điểm $E$ thuộc cạnh $AB$ . Đường phân giác góc $\widehat{CDE}$ cắt $BC$ tại $K$ . Trên tia đối của tia $AB$ lấy điểm $F$ sao cho $AF= CK$ . Tam giác $DEF$ là tam giác gì?
- A.
  Tam giác đều
- B.
  Tam giác cân tại F
- C.
  Tam giác cân tại D
- D.
  Tam giác cân tại E
Hướng dẫn:
Hình vẽ minh họa
Từ giả thiết dễ dàng thấy được hai tam giác ADC và tam giác CDK bằng nhau (c – g – c)
Suy ra $\widehat{ADF} = \widehat{CDK} =\widehat{EDK}$
Từ đó ta có:
$\widehat{KDF} = \widehat{ADF} +\widehat{KDA} = \widehat{CDK} + \widehat{KDA} = 90^{0}(1)$
$\widehat{AFD} + \widehat{ADF} = 90^{0}\Rightarrow \widehat{AFD} + \widehat{KDE} = 90^{0}(2)$
Từ (1) và (2) suy ra $\widehat{EFD} =\widehat{EDF}$ (cùng phụ với góc $\widehat{EDK}$ )
Vậy tam giác DEF cân tại E
Câu 7: Vận dụng
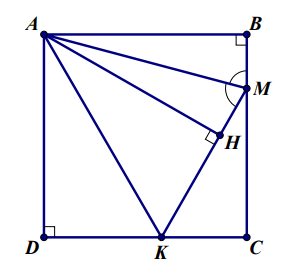
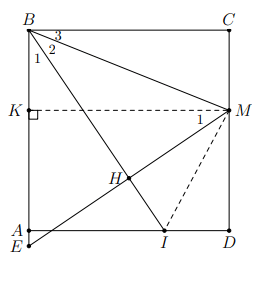
Chọn khẳng định đúng
Cho điểm $M$ thuộc cạnh $CD$ của hình vuông $ABCD$ . Tia phân giác của góc $ABM$ cắt $AD$ ở $I$ . Chọn khẳng định đúng?
- A.
  $BI \geq 3MI$
- B.
  $BI = 3MI$
- C.
  $BI > MI$
- D.
  $BI \leq 2MI$
Hướng dẫn:
Hình vẽ minh họa

Vẽ MH ⊥ BI, MH cắt AB tại E.

Do BI là phân giác ABM nên E đối xứng với M qua BI.

Ta có

$ME = 2MH \leq 2MI(1)$

Kẻ MK ⊥ AB, xét tam giác MKE và tam giác BAI có:

$\left\{ \begin{matrix} \widehat{B_{1}} = \widehat{M_{1}} \\ MK = BA \\ \widehat{K} = \widehat{A} = 90^{0} \\ \end{matrix} ight.\ \Rightarrow \Delta MKE = \Delta BAI \Rightarrow ME = BI(2)$

Từ (1) và (2) suy ra $BI \leq 2MI$
Câu 8: Thông hiểu
Chọn đáp án chính xác
Trong các dấu hiệu nhận biết sau thì dấu hiệu nào không đủ điều kiện để tứ giác là hình vuông?
- A.
  Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.
- B.
  Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
- C.
  Hình bình hành có hai đường chéo bằng nhau là hình vuông.
- D.
  Hình chữ nhật có hai đường chéo vuông gócvới nhau là hình vuông.
Hướng dẫn:
Dấu hiệu nhận biết hình vuông:

Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.
Hình thoi có một góc vuông là hình vuông.
Hình thoi có hai đường chéo bằng nhau là hình vuông.
Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
=> Hình bình hành có hai đường chéo bằng nhau thì không là hình vuông.
Câu 9: Vận dụng
Chọn khẳng định đúng
Ở phía trong của hình vuông $ABCD$ vẽ tam giác $ADE$ cân tại $E$ và có góc ở đáy bằng $15^0$ . Khẳng định nào sau đây đúng?
- A.
  Tam giác BEC đều
- B.
  Tam giác BEC cân
- C.
  Tam giác BEC vuông cân
- D.
  Tam giác BEC vuông
Hướng dẫn:
Hình vẽ minh họa
Ta có: $\widehat{BAE} = 90^{0} -\widehat{DAE} = 75^{0}$
Tương tự $\Delta ABE = \Delta DCE(c - g -c)$
Suy ra $EB = EC$
Bên trong tam giác ABE, dựng tam giác đều AEK.
$\widehat{BAK} = \widehat{BAE} -\widehat{KAE} = 75^{0} - 60^{0} = 15^{0}$
Do đó $\Delta AKB = \Delta AED(c - g -c)$
Tam giác ∆ABK cân tại K, có góc đáy bằng 15⁰, suy ra:
$\left\{ \begin{matrix}\widehat{AKB} = 150^{0} \\\widehat{EKB} = 360^{0} - \left( 60^{0} + 150^{0} ight) = 150^{0} \\\end{matrix} ight.$
Xét ∆ABK và ∆EBK có AK = EK; $\widehat{AKB} = \widehat{EKB} = 150^{0}$ ; BK chung.
Suy ra $∆ABK = ∆EBK (c‐g‐c)$
$=> EB = AB$ .
Vậy ta có $EB = EC = BC$ , nên ∆BCE đều.
Câu 10: Nhận biết
Tính độ dài cạnh hình vuông
Cho hình vuông có chu vi $28 cm$ . Độ dài cạnh hình vuông là:
- A.
  $7 cm$
- B.
  $8 cm$
- C.
  $5 cm$
- D.
  $10 cm$
Hướng dẫn:
Gọi a là độ dài một cạnh hình vuông.

Hình vuông có 4 cạnh bằng nhau nên chu vi hình vuông bằng 4x.

Từ giả thiết ta có

$4x= 28$

$=> x = 7cm$

Vậy cạnh hình vuông là $x = 7cm$
Câu 11: Nhận biết
Hoàn thành dấu hiệu nhận biết
Hình bình hành có 1 góc vuông là:
- A.
  Hình thang cân.
- B.
  Hình thoi
- C.
  Hình chữ nhật
- D.
  Hình vuông
Hướng dẫn:
Hình bình hành có 1 góc vuông là hình chữ nhật.
Câu 12: Thông hiểu
Tính số đo góc MCN
Cho hình vuông $ABCD$ có cạnh bằng $1$ . Gọi $M,N$ là hai điểm lần lượt nằm trên các cạnh $AB,AD$ sao cho chu vi tam giác $AMN$ bằng $2$ . Tính số đo góc $\widehat{MCN}$ .
- A.
  $60^{0}$
- B.
  $90^{0}$
- C.
  $30^{0}$
- D.
  $45^{0}$
Hướng dẫn:
Hình vẽ minh họa
Theo giả thiết:
$2 = AM + AN + MN$
$= (AB – BM) + (AD – DN) + MN$
$= 2 – (BM + DN) + MN$
Suy ra $MN = BM + DN.$
Trên tia đối của tia DN lấy điểm I thỏa mãn $DI = BM$ .
Hai tam giác vuông CBM và CDI bằng nhau vì có: $CB = CD$ ; $\widehat{CBM} = \widehat{CDI} = 90^{0}$ ; BM = DI
Suy ra CM = CI ; $\widehat{BCM} =\widehat{DCI}$
$\widehat{MCI} = \widehat{MCD} +\widehat{DCI} = \widehat{MCD} + \widehat{BCM} = 90^{0}$
Theo trên ta có $MN = BM + DN = ID + DN = IN$ .
Xét hai tam giác CMN và CIN có: $CM = CI; MN = IN$ ; CN chung.
Suy ra $\Delta CMN = \Delta CIN\Rightarrow \widehat{MCN} = \widehat{ICN}$
Mà $\widehat{MCN} + \widehat{ICN} =\widehat{MCI} = 90^{0}$
$\Rightarrow \widehat{MCN} =45^{0}$
Câu 13: Vận dụng
Xác định tứ giác MNPQ
Cho hình bình hành $ABCD$ . Bên ngoài hình bình hành dựng các hình vuông $ABEF,BCGH,CDIJ,ADKL$ . Gọi $M,N,P,Q$ lần lượt là tâm của 4 hình vuông đó. Khi đó tứ giác $MNPQ$ là hình gì?
- A.
  Hình chữ nhật
- B.
  Hình bình hành
- C.
  Hình vuông
- D.
  Hình thoi
Hướng dẫn:
Hình vẽ minh họa

Dễ dàng nhận thấy $CP = BM = AM = DP$ và $CN = BN = AQ = DQ (1)$

Trong bình hành ABCD, đặt $\widehat{BAD} = \widehat{BCD} = x$

Ta có:

$\widehat{PCN} = \widehat{PCD} + \widehat{DCB} + \widehat{BCN}$

$= 45^{0} + x + 45^{0} = x + 90^{0}$

Chứng minh tương tự ta được:

$\widehat{PCN} = \widehat{MBN} = \widehat{MAQ} = \widehat{PDQ} = x + 90^{0}(2)$

Từ (1) và (2) ta có: $\Delta PCN = \Delta MBN = \Delta MAQ = \Delta PDQ$

Suy ra $PN = MN = MQ = PQ$ , hay tứ giác MNPQ là hình thoi.

Lại có $\left\{ \begin{matrix} \widehat{BMN} = \widehat{AMQ} \\ \widehat{BMQ} + \widehat{AMQ} = 90^{0} \\ \end{matrix} ight.\ \Rightarrow \widehat{BMN} + \widehat{BMQ} = 90^{0}$

$\Rightarrow \widehat{NMQ} = 90^{0}$

Vậy tứ giác $MNPQ$ là hình vuông
Câu 14: Nhận biết
Chọn đáp án chính xác
Tứ giác nào không có hai đường chéo bằng nhau?
- A.
  Hình thoi
- B.
  Hình chữ nhật
- C.
  Hình vuông
- D.
  Hình thang cân
Hướng dẫn:
Trong các hình: hình vuông, hình chữ nhật, hình thang cân, hình thoi thì hình thoi là hình có hai đường chéo không bằng nhau.
Câu 15: Thông hiểu
Tính số đo góc KAM
Cho hình vuông $ABCD$ . Gọi $M$ là một điểm tùy ý trên cạnh $BC$ , vẽ đường thẳng cắt cạnh $CD$ tại $K$ sao cho $\widehat{AMB} = \widehat{AMK}$ ; $AH\bot MK$ tại $H$ . Tính số đo góc $\widehat{KAM}$ ?
- A.
  $45^{0}$
- B.
  $90^{0}$
- C.
  $30^{0}$
- D.
  $60^{0}$
Hướng dẫn:
Hình vẽ minh họa

Ta có: $\left\{ \begin{gathered} \widehat {BAM} + \widehat {BMA} = {90^0} \hfill \\ \widehat {HAM} + \widehat {HMA} = {90^0} \hfill \\ \widehat {BMA} = \widehat {HMA} \hfill \\ \end{gathered} ight. \Rightarrow \widehat {BAM} = \widehat {HAM}$

Xét hai tam giác AMH và AMB có:

$\widehat{BAM} = \widehat{HAM}$

$AH$ là cạnh chung

$\widehat{BAM} = \widehat{HMA}$

=> $\Delta AMH = \Delta AMB(g - c - g)$

$\Rightarrow AH = AB$

Xét hai tam giác ADK và AHK lần lượt vuông tại D và H, có cạnh huyền AK chung, đồng thời AH = AD (vì cùng bằng AB).

=> $\Delta ADK = \Delta AHK \Rightarrow \widehat{DAK} = \widehat{HAK}$

$\widehat{KAM} = \widehat{HAK} + \widehat{HAM}$

$= \frac{1}{2}\left( \widehat{HAD} + \widehat{HAB} ight) = \frac{1}{2}\widehat{BAD} = 45^{0}$