Luyện tập Tứ giác Cánh Diều

Câu 1: Thông hiểu

Tính giá trị biểu thức T

Gọi độ dài cạnh của tứ giác $ABCD$ là $a, b, c, d$ . Biết chu vi tứ giác bằng 76cm và $a:b:c:d = 2:5:4:8$ . Tính giá trị biểu thức $T = (a + b)(c + d)$ .

A.
$T = 1435$
B.
$T = 1520$
C.
$T = 1247$
D.
$T = 1344$

Hướng dẫn:

Theo bài ra ta có:

$a:b:c:d = 2:5:4:8$

$\Rightarrow \frac{a}{2} = \frac{b}{5} = \frac{c}{4} = \frac{d}{8} = \frac{a + b + c + d}{2 + 5 + 4 + 8} = \frac{76}{19} = 4$

$\Rightarrow \left\{ \begin{matrix} a = 8 \\ b = 20 \\ c = 16 \\ d = 32 \\ \end{matrix} ight.\ \Rightarrow T = (8 + 20)(16 + 32) = 1344$

Câu 2: Nhận biết

Chọn khẳng định đúng

Các số đo nào dưới đây chỉ bốn góc của một tứ giác?

A.
$95^{0};72^{0};68^{0};135^{0}$
B.
$54^{0};145^{0};105^{0};56^{0}$
C.
$122^{0};92^{0};74^{0};82^{0}$
D.
$67^{0};42^{0};137^{0};120^{0}$

Hướng dẫn:

Dựa vào tính chất tổng bốn góc của một tứ giác bằng 360⁰ ta suy ra dãy số chỉ bốn góc của một tứ giác là: $54^{0};145^{0};105^{0};56^{0}$

Vì $54^{0} + 145^{0} + 105^{0} + 56^{0} = 360^{0}$

Câu 3: Thông hiểu

Tính tổng các góc

Cho hình vẽ sau:

Tính $\widehat{A_{1}} + \widehat{B_{1}} +\widehat{C_{1}} + \widehat{D_{1}} = ?$

A.
$270^{0}$
B.
$180^{0}$
C.
$320^{0}$
D.
$360^{0}$

Hướng dẫn:

Ta có: $\left\{ \begin{matrix}\widehat{A} + \widehat{A_{1}} = 180^{0} \\\widehat{B} + \widehat{B_{1}} = 180^{0} \\\widehat{C} + \widehat{C_{1}} = 180^{0} \\\widehat{D} + \widehat{D_{1}} = 180^{0} \\\end{matrix} ight.$ (vì các cặp góc kề bù nhau)

$\widehat{A} + \widehat{A_{1}} +\widehat{B} + \widehat{B_{1}} + \widehat{C} + \widehat{C_{1}} +\widehat{D} + \widehat{D_{1}} = 4.180^{0}$

$\Rightarrow \left( \widehat{A} +\widehat{B} + \widehat{C} + \widehat{D} ight) + \left( \widehat{A_{1}}+ \widehat{B_{1}} + \widehat{C_{1}} + \widehat{D_{1}} ight) =720^{0}$

Mà $\widehat{A} + \widehat{B} +\widehat{C} + \widehat{D} = 360^{0}$ (tổng bốn góc của một tứ giác)

Khi đó: $\widehat{A_{1}} + \widehat{B_{1}}+ \widehat{C_{1}} + \widehat{D_{1}} = 720^{0} - 360^{0} =360^{0}$

Câu 4: Thông hiểu

Tính độ dài CD

Tứ giác ABCD có hai đường chéo vuông góc, $AB = 8cm,\ BC = 7cm,\ AD = 4cm$ . Tính độ dài CD.

A.
$CD = 1$
B.
$CD = 4$
C.
$CD = 2$
D.
$CD = 3$

Hướng dẫn:

Gọi O là giao điểm của AC và BD.

Ta có $OC^{2} + OD^{2} + OB^{2} + OA^{2} = BC^{2} + AD^{2} = 72 + 42 = 65$

và $OA^{2} + OB^{2} = AB^{2} = 64$

Suy ra $OC^{2} + OD^{2} = 1$ hay $CD^{2} = 1$

Vậy CD = 1

Câu 5: Thông hiểu

Tính số đo góc A và góc C

Cho tứ giác $ABCD$ có $AB = BC; CD = DA$ . Tính số đo các góc $A$ và $C$ biết $\widehat{B} = 100^{0};\widehat{D} = 80^{0}$ .

A.
$\widehat{A} = 60^{0};\widehat{C} = 80^{0}$
B.
$\widehat{A} = 45^{0};\widehat{C} = 30^{0}$
C.
$\widehat{A} = 40^{0};\widehat{C} = 50^{0}$
D.
$\widehat{A} = 90^{0};\widehat{C} = 90^{0}$

Hướng dẫn:

Xét tam giác $ABD$ và tam giác $CBD$ có:

$AB = BC$

$AD = DC$

$BD$ cạnh chung

$\Rightarrow \Delta ABD = \Delta CBD(c - c - c) \Rightarrow \widehat{A} = \widehat{C}$

Mặt khác $\widehat{A} + \widehat{B} + \widehat{C} + \widehat{D} = 360^{0}$

$\Rightarrow \widehat{A} = \widehat{C} = 90^{0}$

Câu 6: Nhận biết

Tính số đo góc D

Cho tứ giác $ABCD$ có $\widehat{A} = 40^{0};\widehat{B} = 54^{0};\widehat{C} = 134^{0}$ . Tính số đo góc $\widehat{D}$ ?

A.
$\widehat{D} = 145^{0}$
B.
$\widehat{D} = 138^{0}$
C.
$\widehat{D} = 120^{0}$
D.
$\widehat{D} = 132^{0}$

Hướng dẫn:

Ta có:

Tổng 4 góc của một tứ giác bằng $360^{0}$ khi đó:

$\widehat{A} + \widehat{B} + \widehat{C} + \widehat{D} = 360^{0}$

$\Rightarrow 40^{0} + 54^{0} + \widehat{D} + 134^{0} = 360^{0}$

$\Rightarrow \widehat{D} = 360^{0} - \left( 40^{0} + 54^{0} + 134^{0} ight) = 132^{0}$

Câu 7: Nhận biết

Ghép nội dung đáp án thích hợp

Cho tứ giác ABCD biết $\widehat{A} = 75^{0};\widehat{B} =90^{0};\widehat{C} = 120^{0}$ .

Góc ngoài tại đỉnh A có số đo là 105||90||60

Góc ngoài tại đỉnh B có số đo là 90||60||105

Góc ngoài tại đỉnh C có số đo là 60||90||105

Góc ngoài tại đỉnh D có số đo là 105||90||65

Đáp án là:

Cho tứ giác ABCD biết $\widehat{A} = 75^{0};\widehat{B} =90^{0};\widehat{C} = 120^{0}$ .

Góc ngoài tại đỉnh A có số đo là 105||90||60

Góc ngoài tại đỉnh B có số đo là 90||60||105

Góc ngoài tại đỉnh C có số đo là 60||90||105

Góc ngoài tại đỉnh D có số đo là 105||90||65

Ta có:

$\widehat{A} + \widehat{B} + \widehat{C}+ \widehat{D} = 360^{0}$

$\Rightarrow \widehat{D} =75^{0}$

Khi đó ta có:

Góc ngoài tại đỉnh A có số đo là $180^{0}- 75 = 105^{0}$

Góc ngoài tại đỉnh B có số đo là $180^{0}- 90^{0} = 90^{0}$

Góc ngoài tại đỉnh C có số đo là $180^{0}- 120^{0} = 60^{0}$

Góc ngoài tại đỉnh D có số đo là $180^{0}- 75^{0} = 105^{0}$

Câu 8: Thông hiểu

Tính số đo góc

Cho hình vẽ:

Tính số đo góc $\widehat{D_{1}}$ ?

A.
$105^{0}$
B.
$124^{0}$
C.
$110^{0}$
D.
$155^{0}$

Hướng dẫn:

Ta có: $\widehat{A} + \widehat{B} +\widehat{C} + \widehat{D} = 360^{0}$

$\Rightarrow \widehat{D} = 360^{0} -\left( \widehat{A} + \widehat{B} + \widehat{C} ight) =75^{0}$

Vì $\widehat{D};\widehat{D_{1}}$ là hai góc kề bù nên $\widehat{D} +\widehat{D_{1}} = 180^{0} \Leftrightarrow \widehat{D_{1}} = 180^{0} -\widehat{D} = 105^{0}$

Câu 9: Vận dụng

Tính số đo góc AIB

Cho tứ giác $ABCD$ biết $\widehat{B} + \widehat{C} = 200^{0}$ ; $\widehat{B} + \widehat{D} = 180^{0}$ ; $\widehat{D} + \widehat{C} = 120^{0}$ . Gọi I là giao điểm của các tia phân giác góc A và góc B. Tính số đo góc $AIB$ ?

A.
$110^{0}$
B.
$96^{0}$
C.
$120^{0}$
D.
$84^{0}$

Hướng dẫn:

Từ giả thiết ta có:

$2\widehat{B} + 2\widehat{C} + 2\widehat{D} = 200^{0} + 180^{0} + 120^{0}$

$\Rightarrow \widehat{B} + \widehat{C} + \widehat{D} = 250^{0}$

Vì $\widehat{A} + \widehat{B} + \widehat{C} + \widehat{D} = 360^{0} \Rightarrow \widehat{A} = 110^{0}$

$\Rightarrow \widehat{B} = 250^{0} - \left( \widehat{C} + \widehat{D} ight) = 250^{0} - 120^{0} = 130^{0}$

Trong tam giác ABI có:

$\widehat{AIB} = 180^{0} - \frac{\widehat{A} + \widehat{B}}{2} = 120^{0}$

Câu 10: Vận dụng

Tính số đo góc ABC

Cho tứ giác ABCD có $AD = DC = CB;\widehat{C} = 130^{0};\widehat{D} = 110^{0}$ . Tính số đo góc $\widehat{ABC}$ .

A.
$\widehat{ABC} = 110^{0}$
B.
$\widehat{ABC} = 55^{0}$
C.
$\widehat{ABC} = 60^{0}$
D.
$\widehat{ABC} = 135^{0}$

Hướng dẫn:

Hình vẽ minh họa

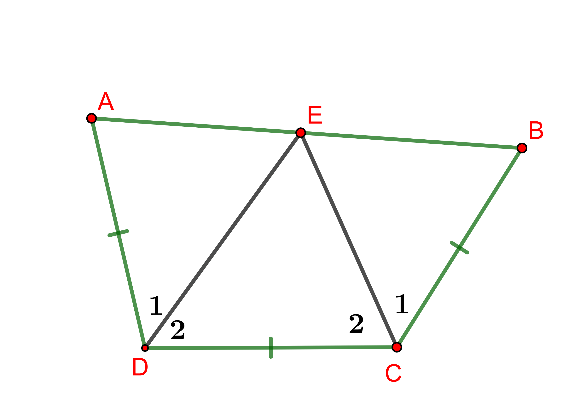
Tính số đo góc ABC

$\Rightarrow \widehat{CED} = 180^{0} - \frac{110^{0} + 130^{0}}{2} = 60^{}$

$\Delta ADE = \Delta CDE(c - g - c) \Rightarrow \widehat{AED} = \widehat{CED} = 60^{0}$

$\Delta BCE = \Delta DCE(c - g - c) \Rightarrow \widehat{BEC} = \widehat{DEC} = 60^{0}$

Suy ra $\widehat{AEB} = 180^{0}$ do đó ba điểm A, E, B thẳng hàng

$\Rightarrow \widehat{ABC} = 360^{0} - \left( 65^{0} + 110^{0} + 130^{0} ight) = 55^{0}$

Câu 11: Vận dụng cao

Tính độ dài cạnh AD

Cho tứ giác $ABCD$ có O là giao điểm hai đường chéo. Tính độ dài cạnh AD biết $AB = 6;OA =8;OB = 4;OD = 6$ .

A.
$AD = 12$
B.
$AD = 3\sqrt{2}$
C.
$AD = \sqrt{166}$
D.
$AD = 9\sqrt{12}$

Hướng dẫn:

Hình vẽ minh họa

Kẻ $AH ⊥ BD$ . Đặt $BH = x, AH = y$ .

Áp dụng định lý Pythagore vào các tam giác vuông ABH và AOH, ta có:

$\left\{ \begin{matrix}x^{2} + y^{2} = 36 \\(x + 4)^{2} + y^{2} = 64 \\\end{matrix} ight.\ \Rightarrow x = \frac{3}{2};y^{2} =\frac{135}{2}$

Áp dụng định lý Pythagore vào các tam giác vuông ADH, ta có:

$AD^{2} = HD^{2} + AH^{2} = 11,5^{2} +\frac{135}{2} = 166$

$\Rightarrow AD = \sqrt{166}$

Câu 12: Vận dụng

Tính độ dài cạnh AD

Cho tứ giác ABCD có hai đường chéo vuông góc. Biết $AB = 3;BC = 6,6;CD = 6$ . Tính độ dài cạnh $AD$ .

A.
$AD = 3,8$
B.
$AD = 1,2$
C.
$AD = 2,4$
D.
$AD = 2$

Hướng dẫn:

Hình vẽ minh họa

Gọi O là giao điểm của hai đường chéo.

Xét ∆AOB, ∆COD vuông tại O, ta có:

$AB^{2} + CD^{2} = OA^{2} + OB^{2} +OC^{2} + OD^{2}$

Chứng minh tương tự, ta được:

$BC^{2} + AD^{2} = OB^{2} + OC^{2} +OA^{2} + OD^{2}$

Do đó:

$AB^{2} + CD^{2} = BC^{2} +AD^{2}$

$\Rightarrow AB^{2} + CD^{2} - BC^{2} =AD^{2}$

$\Rightarrow AD = 1,2$

Chúc mừng Bạn đã hoàn thành bài!

Toán 8 CD

Chương 1: Đa thức nhiều biến

Luyện tập Đơn thức nhiều biến. Đa thức nhiều biến

Luyện tập Các phép toán với đa thức nhiều biến

Luyện tập Hằng đẳng thức đáng nhớ

Luyện tập Vận dụng hằng đẳng thức vào phân tích đa thức thành nhân tử

Ôn tập Chương 1

Đề kiểm tra 15 phút Chương 1 Đa thức nhiều biến

Chương 2: Phân thức đại số

Luyện tập Phân thức đại số

Luyện tập Cộng, trừ phân thức

Luyện tập Nhân, Chia phân thức

Ôn tập chương 2

Chương 3: Hàm số và đồ thị

Luyện tập Hàm số

Luyện tập Mặt phẳng tọa độ. Đồ thị của hàm số

Luyện tập Hàm số bậc nhất y = ax + b

Luyện tập Đồ thị của hàm số bậc nhất y = ax + b (a ≠ 0)

Chương 4: Hình học trực quan

Luyện tập Hình chóp tam giác đều

Luyện tập Hình chóp tứ giác đều

Chương 5: Tam giác. Tứ giác

Luyện tập Định lí Pythagore

Luyện tập Tứ giác

Luyện tập Hình thang cân

Luyện tập Hình bình hành

Luyện tập Hình chữ nhật

Luyện tập Hình thoi

Luyện tập Hình vuông

Đề thi HK1

Đề thi học kì 1 Toán 8 Cánh Diều (Đề 1)

Đề thi học kì 1 Toán 8 Cánh Diều (Đề 2)

Chương 6: Một số yếu tố thống kê và xác suất

Luyện tập Thu thập và phân loại dữ liệu

Luyện tập Mô tả và biểu diễn dữ liệu trên bảng, biểu đồ

Luyện tập Phân tích và xử lí dữ liệu thu được ở dạng bảng, biểu đồ

Luyện tập Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản

Luyện tập Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản

Ôn tập chương 6

Đề thi giữa học kì 2

Đề thi giữa học kì 2 Toán lớp 8 - Đề 1

Đề thi giữa học kì 2 Toán lớp 8 - Đề 2

Đề thi giữa học kì 2 Toán lớp 8 - Đề 3

Đề thi giữa học kì 2 Toán lớp 8 - Đề 4

Đề thi giữa học kì 2 Toán lớp 8 - Đề 5

Chương 7: Phương trình bậc nhất một ẩn

Luyện tập Phương trình bậc nhất một ẩn

Luyện tập Ứng dụng của phương trình bậc nhất một ẩn

Ôn tập chương 7 Phương trình bậc nhất một ẩn

Chương 8: Tam giác đồng dạng. Hình đồng dạng

Luyện tập Định lí Thalès trong tam giác

Luyện tập Ứng dụng của định lí Thalès trong tam giác

Luyện tập Đường trung bình của tam giác

Luyện tập Tính chất đường phân giác của tam giác

Luyện tập Tam giác đồng dạng

Luyện tập Trường hợp đồng dạng thứ nhất của tam giác

Luyện tập Trường hợp đồng dạng thứ hai của tam giác

Luyện tập Trường hợp đồng dạng thứ ba của tam giác

Ôn tập chương 8