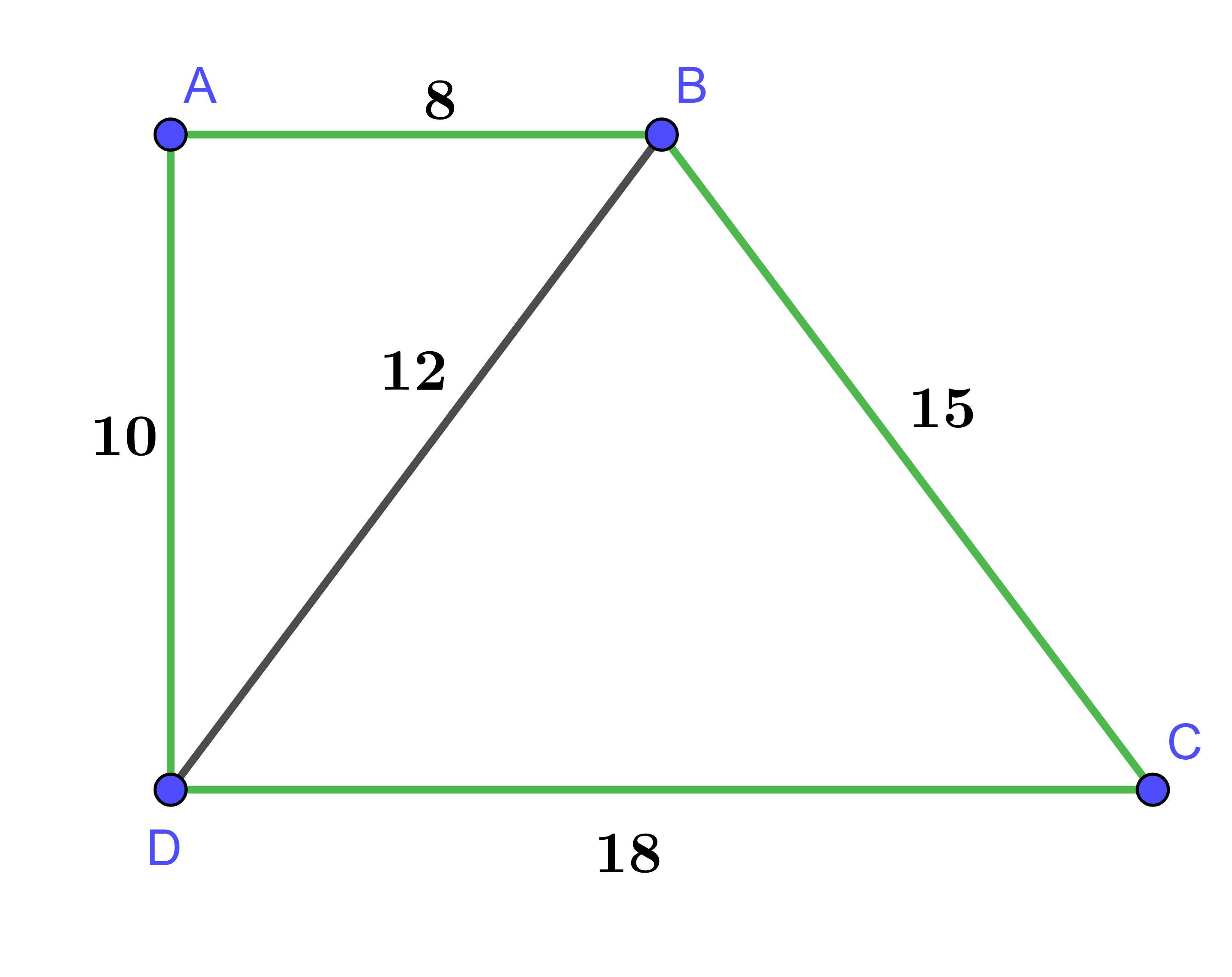
Tứ giác ABCD có ![]() . Chọn câu sai:
. Chọn câu sai:
Hình vẽ minh họa
Ta có:
Mà hai góc này ở vị trí so le trong nên AB // CD.
Vậy ABCD là hình thang.
Ta lại có:
Suy ra tam giác ABD vuông tại A
=> ABCD là hình thang vuông.
Tứ giác ABCD có ![]() . Chọn câu sai:
. Chọn câu sai:
Hình vẽ minh họa

Ta có:
Mà hai góc này ở vị trí so le trong nên AB // CD.
Vậy ABCD là hình thang.
Ta lại có:
Suy ra tam giác ABD vuông tại A
=> ABCD là hình thang vuông.
Cho tam giác ABC nhọn, kẻ đường cao BD và CE. Vẽ các đường cao DF và EG của ΔADE. Tam giác ABD đồng dạng với tam giác nào dưới đây?
Hình vẽ minh họa
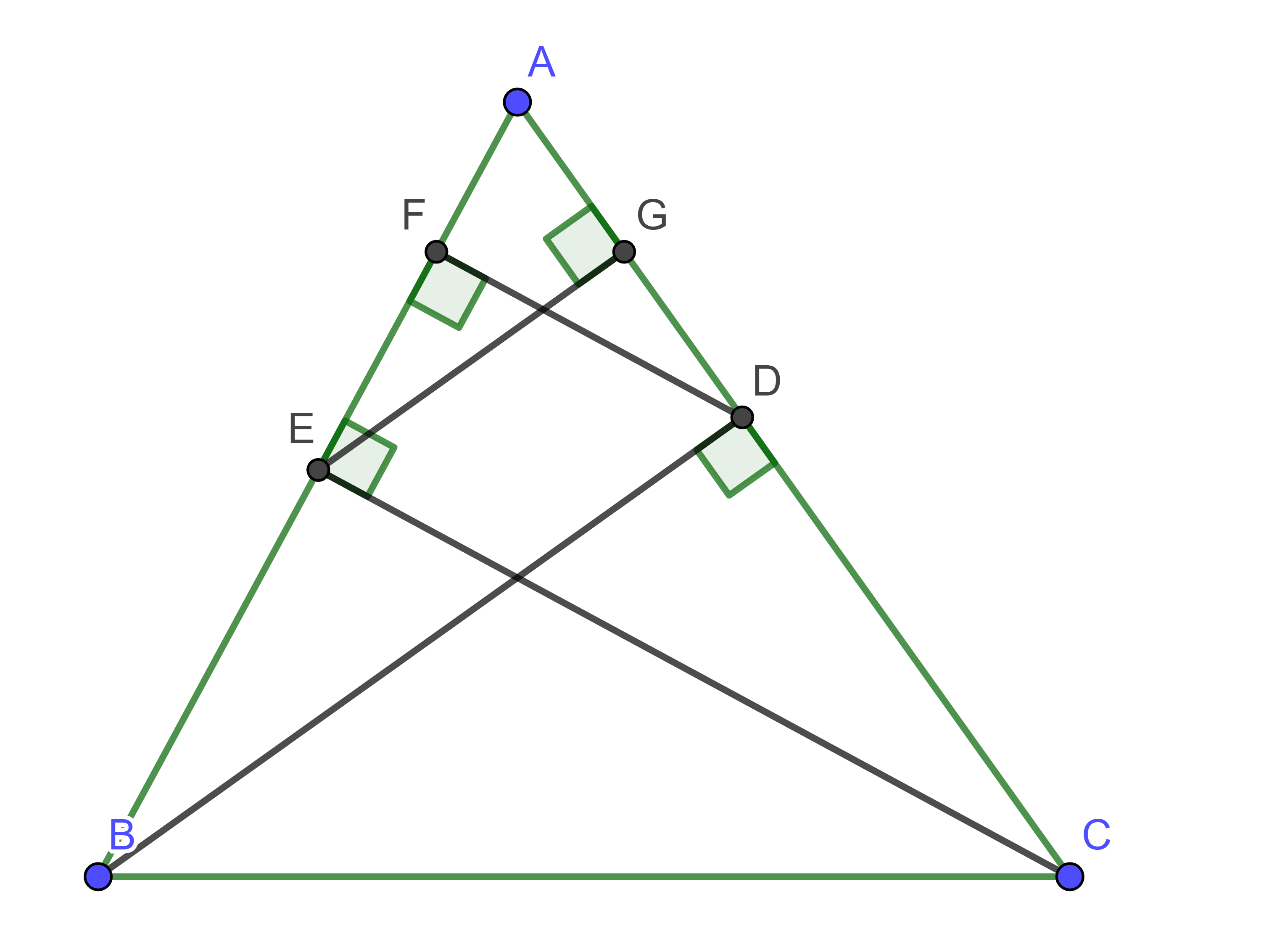
Xét ΔABD và ΔAEG, ta có:
BD ⊥ AC (BD là đường cao)
EG ⊥ AC (EG là đường cao)
=> BD // EG
Theo định lí Thales ta có:
Hai tam giác nào không đồng dạng khi biết độ dài các cạnh của hai tam giác lần lượt là:
Ta có:
=> Hai tam giác 4cm, 5cm, 6cm và 12cm, 15cm, 18cm đồng dạng
=> Hai tam giác 3cm, 4cm, 6cm và 9cm, 12cm, 18cm đồng dạng
=> Hai tam giác 1,5cm, 2cm, 2cm và 1cm, 1cm, 1cm không đồng dạng
=> Hai tam giác 14cm, 15cm, 16cm và 7cm, 7,5cm, 8cm đồng dạng
Hai tam giác nào không đồng dạng khi biết độ dài các cạnh của hai tam giác lần lượt là:
Ta có:
=>
đồng dạng
=>
không đồng dạng
=>
đồng dạng
=>
không đồng dạng
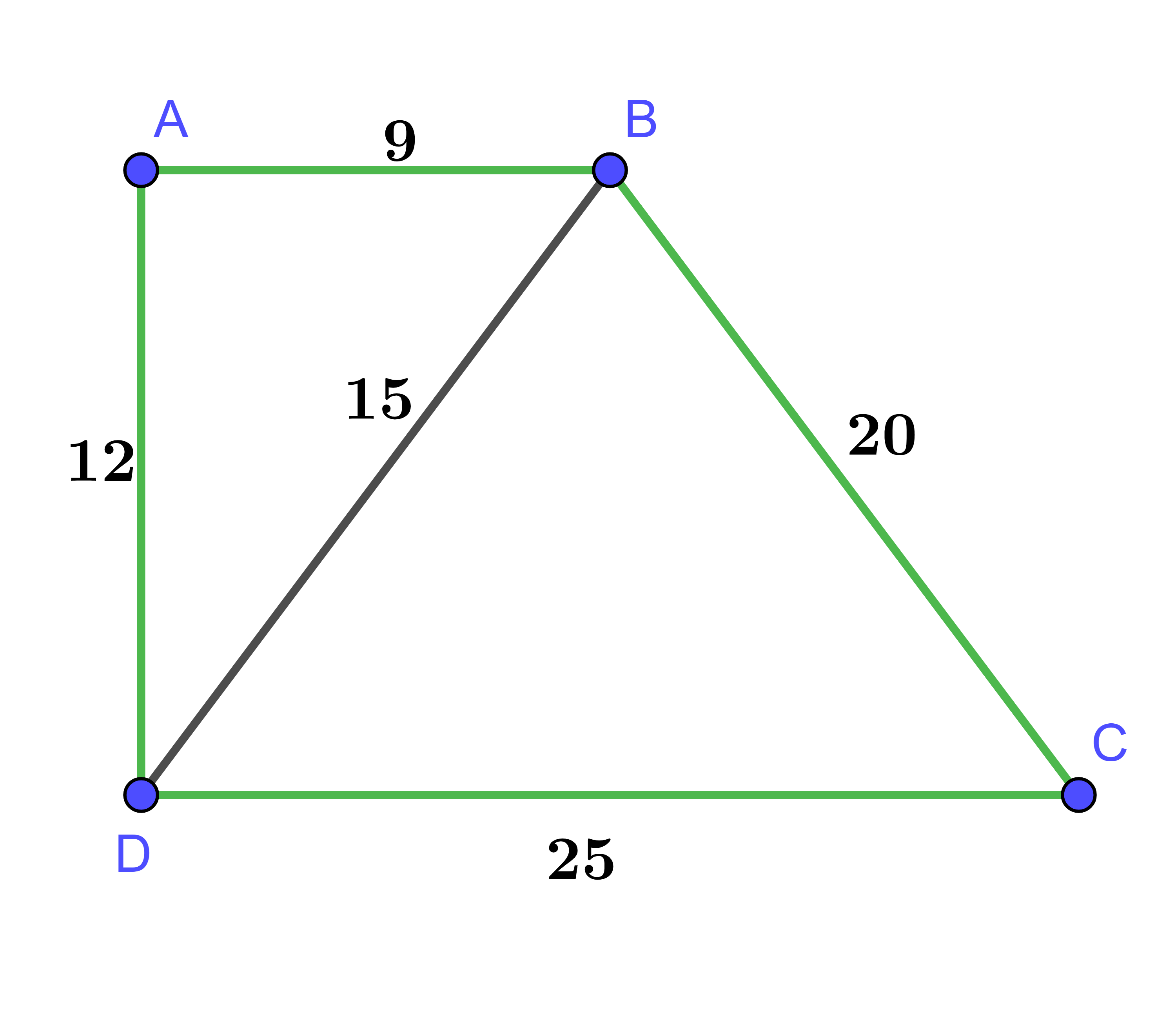
Tứ giác ABCD có ![]() ,
, ![]() . Chọn các đáp án đúng
. Chọn các đáp án đúng
Hình vẽ minh họa
Ta có:
Mà hai góc này ở vị trí so le trong nên AB // CD.
Vậy ABCD là hình thang.
Ta có:
=> Tam giác ABD không vuông
=> ABCD không là hình thang vuông
Dễ thấy tam giác ADC và tam giác ABC không đồng dạng với nhau
Biết ![]() và
và ![]() . Hãy chọn khẳng định sai:
. Hãy chọn khẳng định sai:
Ta có:
Vậy tam giác ABC cân tại A, MNP cân tại M
Vậy đáp án sai là "ΔABC cân tại C".
Một tam giác có cạnh nhỏ nhất bằng 12, hai cạnh còn lại bằng x và y (x < y). Một tam giác khác có cạnh lớn nhất bằng 40,5, hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đó đồng dạng, từ đó suy ra giá trị của S = x + y bằng:
Tam giác thứ nhất có các cạnh là
Tam giác thứ hai có các cạnh là
Vì hai tam giác đồng dạng nên
Cho ![]() . Biết
. Biết ![]() . Hãy chọn câu đúng:
. Hãy chọn câu đúng:
Ta có:
Một tam giác có cạnh nhỏ nhất bằng 8, hai cạnh còn lại bằng x và y; (x < y). Một tam giác khác có cạnh lớn nhất bằng 27, hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đó đồng dạng.
Tam giác thứ nhất có các cạnh là
Tam giác thứ hai có các cạnh là
Vì hai tam giác đồng dạng nên
Cho tam giác ABC có ba góc nhọn, kẻ đường cao BD và CE. Trong tam giác ADE vẽ các đường cao DF và EG. Cho các khẳng định:
(1) ![]()
(2) ![]()
(3) ![]()
Số khẳng định đúng là:
Hình vẽ minh họa

Xét ΔABD và ΔAEG, ta có:
BD ⊥ AC (BD là đường cao)
EG ⊥ AC (EG là đường cao)
=> BD // EG
Theo định lí Thales ta có:
Tương tự ta cũng chứng minh được
không chính xác vì:
Vậy có 2 khẳng định đúng.
