Luyện tập Hình chữ nhật Cánh Diều

Nhận biết Thông hiểu Vận dụng Vận dụng cao

Bài kiểm tra này bao gồm 15 câu
Điểm số bài kiểm tra: 15 điểm
Xem lại kỹ lý thuyết trước khi làm bài
Chuẩn bị giấy và bút để nháp trước khi bắt đầu

Bắt đầu làm bài

00:00:00

Câu 1: Thông hiểu
Xác định tứ giác AHCD
Cho tam giác $ABC$ , đường cao $AH$ . Gọi $I$ là trung điểm của $AC$ . Lấy $D$ là điểm đối xứng với $H$ qua $I$ . Khi đó tứ giác $AHCD$ là hình gì?
- A.
  Hình bình hành
- B.
  Hình thang
- C.
  Hình thang cân
- D.
  Hình chữ nhật
Hướng dẫn:
Hình vẽ minh họa

Ta có $IA = IC$ và $IH = ID$ .

$=> AHCD$ là hình bình hành do có hai đường chéo $AC$ và $DH$ cắt nhau tại trung điểm $I$ .

Mà $\widehat{AHC} = 90^{0}$

$=> AHCD$ là hình chữ nhật.
Câu 2: Thông hiểu
Tính diện tích hình chữ nhật
Tính diện tích của hình chữ nhật có đường chéo $d = 40$ và các cạnh của nó tỉ lệ với hai số 3 và 4?
- A.
  $748$
- B.
  $720$
- C.
  $768$
- D.
  $756$
Hướng dẫn:
Gọi chiều dài và chiều rộng của hình chữ nhật là a và b, (a > b > 0)
Theo đề bài ta có: $\left\{ \begin{gathered} {a^2} + {b^2} = {d^2} = 1600 \hfill \\ \frac{a}{4} = \frac{b}{3} \hfill \\ \end{gathered} ight. \Rightarrow \left\{ \begin{gathered} a = 32 \hfill \\ b = 24 \hfill \\ \end{gathered} ight.$
Vậy $S = 32.24 = 768$ .
Câu 3: Thông hiểu
Tính độ dài đường trung tuyến AO
Cho tam giác $ABC$ vuông tại $A$ có $AB = 4cm; AC = 3cm$ . Khi đó độ dài trung tuyến $AO$ của tam giác $ABC$ là:
- A.
  $2,5$
- B.
  $3$
- C.
  $1,5$
- D.
  $5$
Hướng dẫn:
Áp dụng định lí Pythagore cho tam giác $ABC$ vuông tại $A$ ta có

$AB^{2} + AC^{2} = BC^{2} \Rightarrow BC = 5(cm)$

Vì $AO$ là trung tuyến trong tam giác vuông $ABC$ nên

$AO = \frac{1}{2}BC = \frac{5}{2}(cm)$
Câu 4: Thông hiểu
Tìm giá trị của x
Tính độ dài cạnh CD trong hình vẽ sau:
- A.
  $CD = 10cm$
- B.
  $CD = 15cm$
- C.
  $CD = 9cm$
- D.
  $CD = 13cm$
Hướng dẫn:
Hình vẽ minh họa
Kẻ BH ⊥ DC ta có ABHD là hình chữ nhật nên DH = AB = 7 cm, BH = AD = 8 cm.
Tam giác BHC vuông tại H có
$HC = \sqrt{BC^{2} - BH^{2}} =6cm$
$\Rightarrow DC = DH + HC =13cm$
$=> x = 13cm$
Câu 5: Nhận biết
Chọn đáp án thích hợp
Hình chữ nhật không có:
- A.
  Hai đường chéo vuông góc với nhau
- B.
  Hai đường chéo giao nhau tại trung điểm mỗi đường
- C.
  Bốn góc
- D.
  Các cạnh đối bằng nhau
Hướng dẫn:
Hình chữ nhật không có hai đường chéo vuông góc với nhau.
Câu 6: Vận dụng cao
Tính giá trị nhỏ nhất của tổng S
Cho tam giác $ABC$ vuông tại $A$ . Gọi $O$ là một giao điểm bất kì trong tam giác. Vẽ $OD\bot AB;OE\bot BC;OF\bot AC$ . Tìm giá trị nhỏ nhất của tổng $S = OD^{2} + OE^{2} + OF^{2}$ .
- A.
  $\frac{AH^{2}}{2}$
- B.
  $AH^{2}$
- C.
  $\frac{AH^{2}}{4}$
- D.
  $\frac{AH^{2}}{3}$
Hướng dẫn:
Hình vẽ minh họa

Vẽ $AH\bot BC;OK\bot AH$

Tứ giác $ADOF; KOEH$ là hình chữ nhật nên $OF = AD; OE = HK$

Xét tam giác AOD vuông tại D ta có:

$OD^{2} + AD^{2} = OA^{2} \geq AK^{2}$

Do đó:

$OD^{2} + OF^{2} + OE^{2}$

$= OD^{2} + AD^{2} + OE^{2}$

$\geq AK^{2} + KH^{2} \geq \frac{(AK + KH)^{2}}{2} = \frac{AH^{2}}{2}$

Dấu bằng xảy ra khi O nằm giữa A và H và $AK = KH$

=> O là trung điểm của AH.

Vậy giá trị nhỏ nhất của tổng S là $\frac{AH^{2}}{2}$ khi O là trung điểm của AH.
Câu 7: Thông hiểu
Tính số đo góc BMK
Gọi $H$ là hình chiếu vuông góc của đỉnh $B$ lên đường chéo $AC$ của hình chữ nhật $ABCD$ và $M, K$ lần lượt là trung điểm của . Tính số đo góc $\widehat{BMK}$ .
- A.
  $60^{0}$
- B.
  $100^{0}$
- C.
  $90^{0}$
- D.
  $120^{0}$
Hướng dẫn:
Hình vẽ minh họa

Vì ABCD là hình chữ nhật và I, K lần lượt là trung điểm của AB, CD nên BIKC là hình chữ nhật.

Do đó O là trung điểm của CI, BK.

Xét tam giác IMC vuông tại M có

$MO = \frac{1}{2}IC$

Xét tam giác MBK có $MO = \frac{1}{2}IC = \frac{1}{2}BK$

$\Rightarrow \widehat{BMK} = 90^{0}$
Câu 8: Thông hiểu

Điền đáp án vào chỗ trống

Cho hình chữ nhật $ABCD$ biết rằng đường vuông góc $AH$ kẻ từ $A$ đến $BD$ chia thành hai đoạn $HD = 9cm,HB = 16cm$ . Khi đó:

Độ dài cạnh AB là: 20 $cm$

Độ dài cạnh AD là: 15 $cm$

Đáp án là:

Cho hình chữ nhật $ABCD$ biết rằng đường vuông góc $AH$ kẻ từ $A$ đến $BD$ chia thành hai đoạn $HD = 9cm,HB = 16cm$ . Khi đó:

Độ dài cạnh AB là: 20 $cm$

Độ dài cạnh AD là: 15 $cm$

Hình vẽ minh họa:

Ta có $BD = BH + HD = 16 + 9 = 25 cm$

Xét tam giác $ABD$ vuông tại $A$ có

$AB^{2} + AD^{2} = 25^{2} = 625\ \ (1)$

Xét tam giác $AHD$ vuông tại $H$ có

$AH^{2} + HD^{2} = AD^{2} \Rightarrow AD^{2} = AH^{2} + 9^{2}\ \ (2)$

Xét tam giác $AHB$ vuông tại H có:

$AH^{2} + HB^{2} = AB^{2} \Rightarrow AB^{2} = AH^{2} + 16^{2}\ \ (3)$

Từ (2) và (3) ta có: $AB^{2} - AD^{2} = 16^{2} - 9^{2} = 175\ \ (4)$

Từ (1) và (4) suy ra

$AB^{2} = \frac{625 + 175}{2} = 400 \Rightarrow AB = 20(cm)$

$AD^{2} = \frac{625 - 175}{2} = 225 \Rightarrow AD = 15(cm)$
Câu 9: Vận dụng
Tính tỉ số độ dài hai cạnh ED và EF
Cho hình vuông $ABCD$ có $\widehat{A} = \widehat{D} = 90^{0};AB = AD =\frac{CD}{2}$ . Qua điểm $E$ thuộc cạnh $AB$ , kẻ đường thẳng vuông góc với $DE$ , cắt $BC$ tại $F$ . Tính tỉ số độ dài hai cạnh $ED$ và $EF$ .
- A.
  $\frac{ED}{EF} =\frac{1}{2}$
- B.
  $\frac{ED}{EF} =\frac{2}{3}$
- C.
  $\frac{ED}{EF} = 1$
- D.
  $\frac{ED}{EF} = 2$
Hướng dẫn:
Hình vẽ minh họa
Kẻ $BH ⊥ CD$ tại H $=> ABHD$ là hình vuông, do đó $BH = a$ và $DH = a$
$=> CH = a$
Ta có $BH = HD = CH = a$
=> Tam giác BCD vuông tại B. Gọi M là trung điểm của DF, ta có: $EM = BM = \frac{DF}{2}$
=> Các tam giác MEB, MFB cân tại M.
Vì ABHD là hình vuông nên $\widehat{DBH} =45^{0} \Rightarrow \widehat{ABC} = 135^{0}$
Lại có: $\widehat{MEB} + \widehat{MFB} =\widehat{MBE} + \widehat{MBF} = \widehat{EBF} = 135^{0}$
Do đó $\widehat{EMF} = 360^{0} - 3.135^{0}= 90^{0}$
Xét tam giác DEF có EM là trung tuyến, đồng thời là đường cao nên tam giác DEF cân tại E nên $ED = EF$ .
Câu 10: Thông hiểu
Xác định tam giác EFG
Cho hình thang cân $ABCD$ có $AB // CD$ ; $\widehat{ACD} = 60^{0}$ . Gọi O là giao điểm hai đường chéo. Các điểm $E, F, G$ lần lượt là trung điểm của $OA, OD, BC$ . Tam giác $EFG$ là tam giác gì?
- A.
  Tam giác vuông
- B.
  Tam giác vuông cân
- C.
  Tam giác cân
- D.
  Tam giác đều
Hướng dẫn:
Hình vẽ minh họa

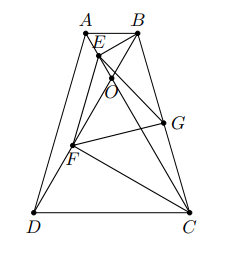
Vì $ABCD$ là hình thang cân nên .

Mà $\widehat {ACD} = {60^0} \Rightarrow \widehat {BCD} = {60^0}$

Khi đó các tam giác $OAB, OCD$ là các tam giác đều.

Vì $E, F$ lần lượt là trung điểm của $OA, OD$ nên $\left\{ \begin{gathered} BE \bot OA;CF \bot OD \hfill \\ EF = \frac{1}{2}AD = \frac{1}{2}BC \hfill \\ \end{gathered} ight.\left( 1 ight)$

Xét các tam giác $BEC, BFC$ lần lượt vuông tại $E, F$ có $G$ là trung điểm của $BC$ nên $EG = FG = \frac{1}{2}BC{\text{ }}\left( 2 ight)$

Từ (1) và (2) suy ra $\Delta EFG$ là tam giác đều.
Câu 11: Nhận biết
Điền cụm từ còn thiếu vào chỗ trống
Hình chữ nhật có .................................. là hình vuông
- A.
  Hai đường chéo bằng nhau.
- B.
  Hai đường chéo cắt nhau.
- C.
  Hai cạnh đối bằng nhau.
- D.
  Hai đường chéo vuông góc.
Hướng dẫn:
Tù cần điền vào chỗ trống là: "Hai đường chéo vuông góc."
Câu 12: Thông hiểu
Xác định tứ giác DMNC
Cho hình chữ nhật $ABCD$ . Tia phân giác góc A cắt tia phân giác góc $D$ tại $M$ , tia phân giác góc $B$ cắt tia phân giác góc $C$ tại $N$ . Gọi $E, F$ lần lượt là giao điểm $DM, CN$ với $AB$ . Xác định tứ giác $DMNC$ ?
- A.
  Hình bình hành
- B.
  Hình thang cân
- C.
  Hình thang
- D.
  Hình chữ nhật
Hướng dẫn:
Hình vẽ minh họa

Dễ thấy các tam giác $ADM, BCN, AME, BNF$ là các tam giác vuông cân với các đỉnh lần lượt là $M, N, M, N$ .

$=> AM = DM = EM$ và $BN = CN = FN$ .

Mặt khác, vì $AD = BC$ nên $\Delta AMD = \Delta CNB \Rightarrow AM = BN$

Vậy $AM = DM = EM = BN = CN = FN$

Tam giác ADE vuông tại A có $\widehat{ADE} = 45^{0} \Rightarrow \widehat{AED} = 45^{0}$

Lại có $\widehat{ABN} = 45^{0} \Rightarrow BN//EM$

Theo trên $BN = EM$ , do vậy $BNME$ là hình bình hành, suy ra $MN // BE // CD$ .

Mặt khác $CN = DM$ . Vậy $CDMN$ là hình thang cân.
Câu 13: Thông hiểu
Tính số đo góc AHM
Cho tam giác $ABC$ vuông tại $A$ , $(AC > AB)$ , đường cao $AH$ . Trên tia $HC$ lấy điểm $D$ sao cho $HD = HA$ , đường thẳng vuông góc với $BC$ tại $D$ cắt $AC$ tại $E$ . Gọi $M$ là trung điểm của $BE$ . Tính số đo góc $\widehat{AHM}$
- A.
  $60^{0}$
- B.
  $90^{0}$
- C.
  $45^{0}$
- D.
  $30^{0}$
Hướng dẫn:
Hình vẽ minh họa:

Dựng $AI\bot DE$ , $I$ thuộc $DE$ .

Ta có AHDI là hình chữ nhật.

Suy ra $AI = HD = AH$ .

Ta có tam giác DBE vuông tại D, tam giác ABE vuông tại A.

Vì M là trung điểm của BE nên $AM = DM = 1/2 BE$

Từ đó dễ dàng thấy được $\Delta AMH = \Delta DMH(c - c - c)$

Suy ra $\widehat{MHA} = \widehat{MHD} = 45^{0}$
Câu 14: Vận dụng
Tính số đo hóc AOD
Cho tam giác $ABC$ vuông tại $A$ , đường cao $AH$ , $I$ là trung điểm của $BC$ . Kẻ $HD\bot AB$ tại $D$ , $HE\bot AC$ tại $E$ . Gọi $O$ là giao điểm của $DE$ và $AI$ . Tính số đo góc $\widehat{AOD}$ .
- A.
  $\widehat{AOD} = 120^{0}$
- B.
  $\widehat{AOD} = 60^{0}$
- C.
  $\widehat{AOD} = 30^{0}$
- D.
  $\widehat{AOD} = 90^{0}$
Hướng dẫn:
Hình vẽ minh họa

Vì tam giác $ABC$ vuông tại $A$ nên $AI = IB = IC$ . Do đó $\widehat{ABI} = \widehat{DAI}(1)$

Dễ thấy $ADHE$ là hình chữ nhật ( $\widehat{A} = \widehat{D} = \widehat{H} = 90^{0}$ )

Suy ra $\widehat{ADE} = \widehat{AHE} = \widehat{BHD}$ (cùng phụ với $\widehat{AHD}$ ) (2)

Mặt khác $\widehat{ABI} + \widehat{DHB} = 90^{0}(3)$

Từ (1), (2), (3) suy ra $\widehat{ADE} + \widehat{DAI} = 90^{0}$

Vậy $\widehat{DOA} = 90^{0}$
Câu 15: Thông hiểu
Tính diện tích hình chữ nhật
Tính diện tích hình chữ nhật biết rằng đường vuông góc kẻ từ $A$ đến $BD$ chia $BD$ thành hai đoạn thẳng có độ dài lần lượt là $9cm$ và $16cm$ ?
- A.
  $S = 230cm^{2}$
- B.
  $S = 360cm^{2}$
- C.
  $S = 250cm^{2}$
- D.
  $S = 300cm^{2}$
Hướng dẫn:
Giả sử $AH$ vuông góc với DB tại H

Ta có: $HD = 9cm, HB = 16cm$

Lại có $AB^{2} + AD^{2} = 25^{2}$

Tam giác ABH $\left( \widehat{H} = 90^{0} ight) \Rightarrow AB^{2} = AH^{2} + 16^{2}(1)$

Tam giác ADH $\left( \widehat{H} = 90^{0} ight) \Rightarrow AD^{2} = AH^{2} + 9^{2}(2)$

Từ (1) và (2) $\Rightarrow \left\{ \begin{matrix} AB^{2} - AD^{2} = 16^{2} - 9^{2} = 175 \\ AB^{2} + AD^{2} = 625 \\ \end{matrix} ight.$

$\Rightarrow \left\{ \begin{matrix} AB = 20cm \\ AD = 15cm \\ \end{matrix} ight.$

Vậy diện tích hình chữ nhật là $S = 300cm^{2}$