Cho tam giác ![]() có
có ![]() . Khi đó tỉ số
. Khi đó tỉ số ![]() bằng bao nhiêu?
bằng bao nhiêu?
Hình vẽ minh họa:
Kẻ đường phân giác BD của tam giác ABC
Khi đó
Ta có:
Xét tam giác ABC và tam giác ADB có
Góc A chung
Cho tam giác ![]() có
có ![]() . Khi đó tỉ số
. Khi đó tỉ số ![]() bằng bao nhiêu?
bằng bao nhiêu?
Hình vẽ minh họa:
Kẻ đường phân giác BD của tam giác ABC
Khi đó
Ta có:
Xét tam giác ABC và tam giác ADB có
Góc A chung
Cho tam giác ABC có ![]() . Điểm D thuộc cạnh AB sao cho
. Điểm D thuộc cạnh AB sao cho ![]() . Điểm E thuộc cạnh AC sao cho
. Điểm E thuộc cạnh AC sao cho ![]() . Chọn câu đúng.
. Chọn câu đúng.
Ta có:
Xét tam giác AED và tam giác ABC có:
Góc A chung
Cho hình vẽ:

Biết M là trung điểm của BC. Tính độ dài cạnh AD?
Ta có: M là trung điểm của BC nên
D là trung điểm của BM nên
Xét tam giác BAD và tam giác BCA ta có:
Góc B chung
Cho tam giác ABC có ![]() . Điểm D thuộc cạnh BC sao cho
. Điểm D thuộc cạnh BC sao cho ![]() . Tính độ dài AD.
. Tính độ dài AD.
Hình vẽ minh họa
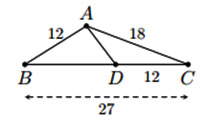
Xét tam giác CAD và tam giác CBA có:
Góc C chung
Cho hình thang ABCD có ![]() . Độ dài BC là:
. Độ dài BC là:
Hình vẽ minh họa
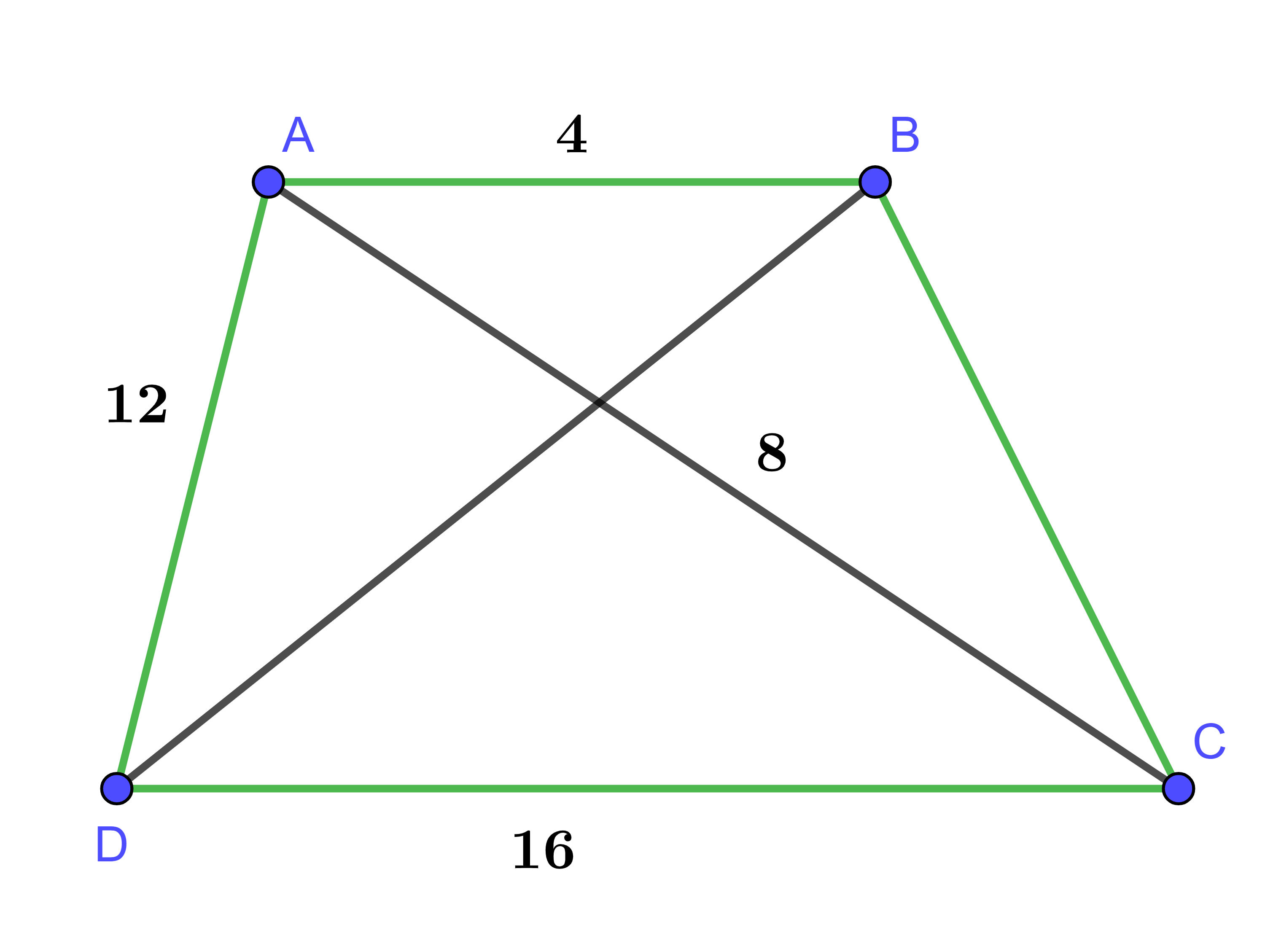
Ta có:
Xét ΔABC và ΔCAD có:
Cho tam giác ![]() có
có ![]() . Trên tia đối của tia
. Trên tia đối của tia ![]() lấy điểm
lấy điểm ![]() sao cho
sao cho ![]() . Tìm tỉ số giữa hai góc
. Tìm tỉ số giữa hai góc ![]() và
và ![]() ?
?
Hình vẽ minh họa
Ta có
Xét tam giác BAC và tam giác BCE ta có
Góc B chung
Ta có
=> Tam giác ACE cân tại A.
Từ (*) và (**) ta có:
Mặt khác
Suy ra
Cho tam giác nhọn ABC có ![]() . Vẽ hình bình hành ABCD. Gọi AH, AK theo thứ tự là các đường cao của các tam giác ABC, ACD. Tính số đo góc AKH.
. Vẽ hình bình hành ABCD. Gọi AH, AK theo thứ tự là các đường cao của các tam giác ABC, ACD. Tính số đo góc AKH.
Hình vẽ minh họa
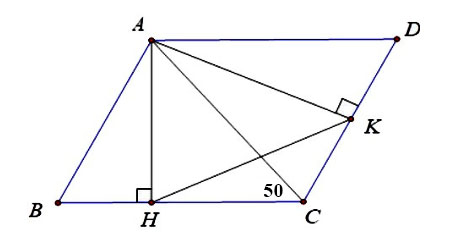
Ta có:
Lại có: (Vì ABCD là hình bình hành)
Mà
(Vì cùng phụ với góc BAH)
Xét tam giác AKH và tam giác BCA có:
Cho tam giác ABC có ![]() . Trên đường thẳng nối hai điểm A, B lấy điểm D sao cho B là điểm nằm giữa và BC = BD. Chọn kết luận đúng.
. Trên đường thẳng nối hai điểm A, B lấy điểm D sao cho B là điểm nằm giữa và BC = BD. Chọn kết luận đúng.
Hình vẽ minh họa
Ta có:
Xét tam giác ABC và ACD có:
Góc A chung
Ta có: => Tam giác BCD là tam giác cân
Lại có:
Cho đoạn thẳng ![]() , gọi
, gọi ![]() là trung điểm của
là trung điểm của ![]() . Trên tia đối của tia
. Trên tia đối của tia ![]() lấy điểm
lấy điểm ![]() sao cho
sao cho ![]() . Vẽ điểm
. Vẽ điểm ![]() sao cho
sao cho ![]() . Tính độ dài
. Tính độ dài ![]() ?
?
![]() a
a
Cho đoạn thẳng , gọi
là trung điểm của
. Trên tia đối của tia
lấy điểm
sao cho
. Vẽ điểm
sao cho
. Tính độ dài
?
a
Hình vẽ minh họa
Ta có:
M là trung điểm của AB =>
Xét tam giác MAD và tam giác DAC ta có
Góc A chung
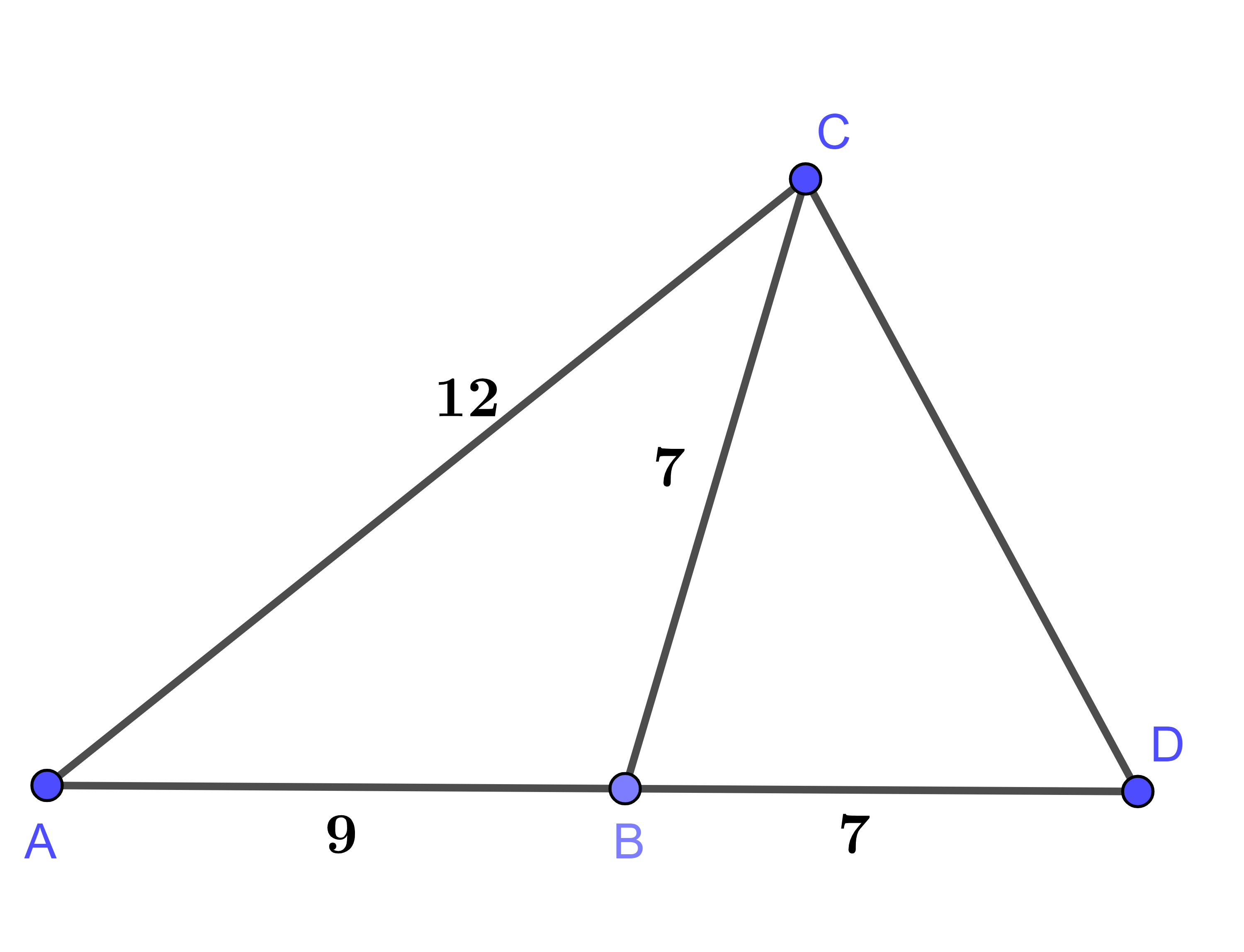
Cho tam giác ABC có AB = 8cm, AC = 16cm. Điểm D thuộc cạnh AB sao cho BD = 2cm. Điểm E thuộc cạnh AC sao cho CE = 13cm. Chọn câu sai.
Hình vẽ minh họa
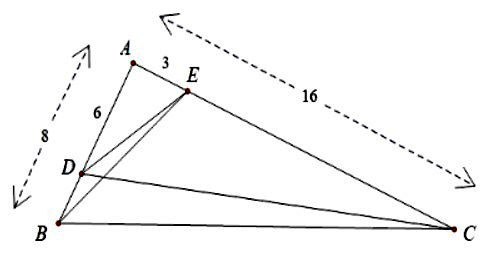
Xét ΔABE và ΔACD có
Góc A chung
Ta có:
Xét tam giác AED và tam giác ABC có:
Góc A chung
Vậy đáp án sai là:
Cho hình vẽ:

Tính độ dài cạnh AD?
Xét tam giác CAD và tam giác CBA ta có:
Góc C chung
Cho tam giác nhọn ABC có ![]() . Vẽ hình bình hành ABCD. Gọi
. Vẽ hình bình hành ABCD. Gọi ![]() theo thứ tự là các đường cao của các tam giác
theo thứ tự là các đường cao của các tam giác ![]() . Tính số đo góc
. Tính số đo góc ![]() .
.
Hình vẽ minh họa
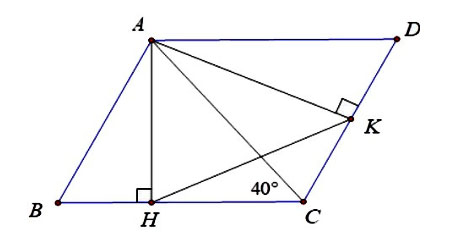
Ta có:
Lại có: (Vì ABCD là hình bình hành)
Mà
(Vì cùng phụ với góc BAH)
Xét tam giác AKH và tam giác BCA có:
Hãy chỉ ra cặp tam giác đồng dạng với nhau từ các tam giác sau đây:
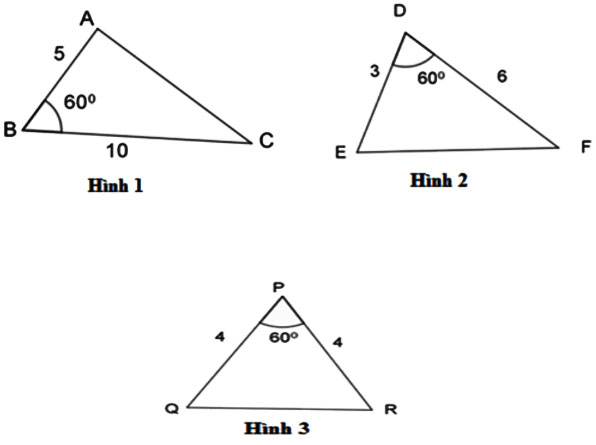
Ta có:
Xét tam giác ABC và tam giác EDF ta có:
Vậy cặp tam giác đồng dạng là Hình 1 và Hình 2.
Cho hình thang vuông ![]() có
có ![]() .
.
Tam giác ABD đồng dạng với tam giác nào dưới đây?
Hình vẽ minh họa
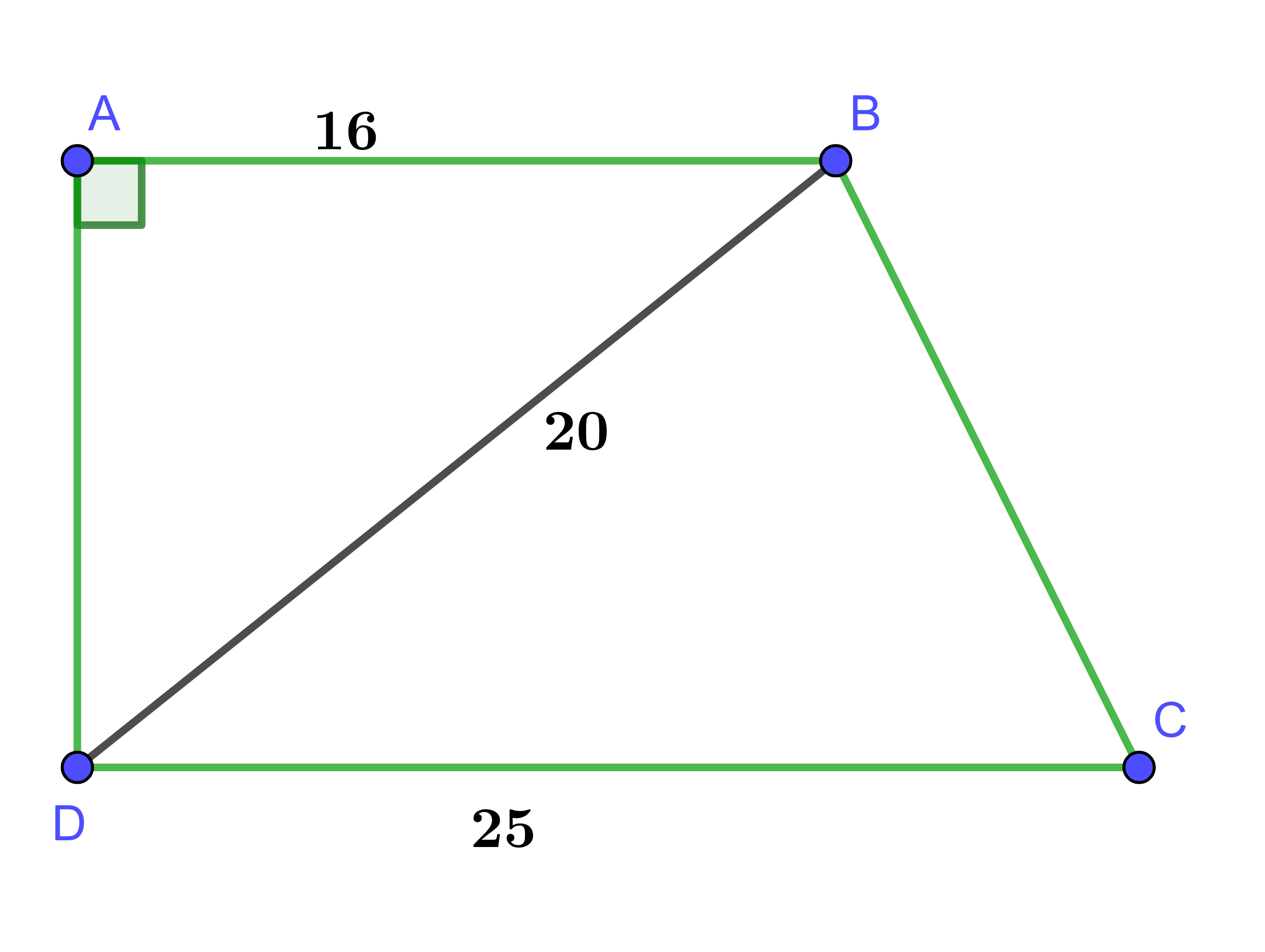
Xét ΔABD và ΔBDC có:
(hai góc ở vị trí so le trong bằng nhau do AB // CD)
Cho tam giác ABC vuông tại A, gọi H là hình chiếu của A lên BC. Dựng hình bình hành ABCD. Chọn kết luận không đúng:
Hình vẽ minh họa
Xét tam giác ABC và tam giác CDA có:
AB = CD (tính chất)
Cạnh AC chung
Vậy ΔABC = ΔCDA đúng
Ta lại có:
Xét ΔABC và ΔHAC có:
Vậy ΔABC ~ ΔHCA sai
Ta có:
và
hay ΔADC ~ ΔCAH nên ΔADC ~ ΔCAH đúng
Có
Xét ΔABH và ΔCBA có:
Góc B chung
Mà ΔADC = ΔCBA nên ΔABH ~ ΔADC hay ΔABH ~ ΔADC đúng.
