Cho tam giác ![]() có
có ![]() . Tính độ dài
. Tính độ dài ![]() ?
?
Hình vẽ minh họa
Trên tia đối của tia BA lấy .
Suy ra tam giác BCD cân tại B.
(vì
là góc ngoài tại đỉnh B)
Xét tam giác ACD và tam giác ABC có:
Góc chung
Cho tam giác ![]() có
có ![]() . Tính độ dài
. Tính độ dài ![]() ?
?
Hình vẽ minh họa
Trên tia đối của tia BA lấy .
Suy ra tam giác BCD cân tại B.
(vì
là góc ngoài tại đỉnh B)
Xét tam giác ACD và tam giác ABC có:
Góc chung
Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của AB và CD. Chọn câu trả lời đúng?
Hình vẽ minh họa
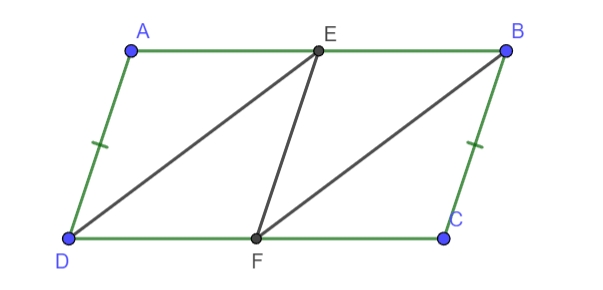
Do ABCD là hình bình hành nên AD = CB, AB = DC;
Mà E, F là trung điểm của AB và CD nên AE = EB = CF = FD
Xét tam giác ADE và tam giác CBF ta có:
AD = CB
AE = CF
Suy ra (c - g - c)
Cho ΔABC có các đường cao BD và CE cắt nhau tại H. Gọi M là giao của AH với BC.
ΔHBE ~ΔHCD||ΔACE
ΔABD ~ΔACE||ΔHCD
Cho ΔABC có các đường cao BD và CE cắt nhau tại H. Gọi M là giao của AH với BC.
ΔHBE ~ΔHCD||ΔACE
ΔABD ~ΔACE||ΔHCD
Hình vẽ minh họa
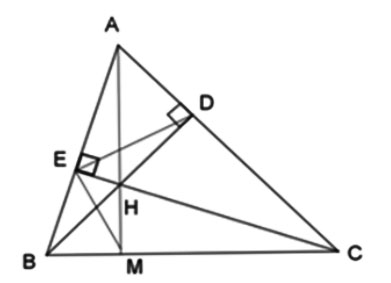
Xét ΔHBE và ΔHCD có:
Xét ΔABD và ΔACE có:
Góc A chung
Cho tam giác ![]() . Kẻ đường phân giác
. Kẻ đường phân giác ![]() . Đường trung trực của
. Đường trung trực của ![]() cắt
cắt ![]() ở
ở ![]() . Biết rằng
. Biết rằng ![]() . Tính độ dài cạnh
. Tính độ dài cạnh ![]() ?
?
Kết quả: 4cm
Cho tam giác . Kẻ đường phân giác
. Đường trung trực của
cắt
ở
. Biết rằng
. Tính độ dài cạnh
?
Kết quả: 4cm
Hình vẽ minh họa
Do K thuộc đường trung trực của AD nên .
Suy ra tam giác KAD cân tại K
(
là góc ngoài tại đỉnh D của tam giác DAC)
Mà (AD là phân giác tam giác ABC) nên
Xét tam giác KAB và tam giác KCA ta có:
Góc chung
Mà (AD là phân giác tam giác ABC)
mà
Cho hình bình hành ABCD, điểm F trên cạnh BC. Tia AF cắt BD và DC lần lượt ở E và G. Chọn khẳng định sai.
Hình vẽ minh họa
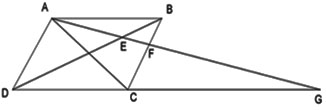
Ta có: ABCD là hình bình hành
Xét tam giác BFE và tam giác DAE có:
Xét tam giác DGE và tam giác BAE có:
Vậy khẳng định sai là: ΔBFE ~ ΔDEA
Cho hình bình hành ABCD có I là giao điểm của AC và BD. E là một điểm bất kì thuộc BC, qua E kẻ đường thẳng song song với AB và cắt BD, AC, AD tại G, H, F. Chọn kết luận sai?
Hình vẽ minh họa
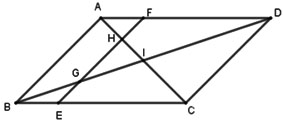
Ta có: ABCD là hình bình hành
Xét ΔBGE và ΔDGF có:
Xét ΔAHF và ΔCHE có:
Lại có GH // AB =>
Xét ΔGHI và ΔBAI có
Góc I chung
Vậy đáp án sai là ΔBGE ~ ΔHGI
Cho tam giác ABC cân tại A, M là trung điểm của BC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho DM là tia phân giác của BDE. Chọn kết luận đúng.
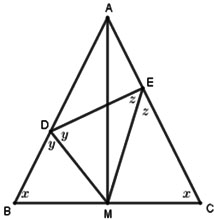
Xét tứ giác BDCE có:
Xét ΔBDM và ΔCME có:
Nếu 2 tam giác ABC và DEF có ![]() =
= ![]() ,
, ![]() =
= ![]() thì:
thì:
Xét ΔABC và ΔDEF có:
=
=
Cho tam giác ![]() . Kẻ đường phân giác
. Kẻ đường phân giác ![]() có
có ![]() . Kẻ tia
. Kẻ tia ![]() sao cho
sao cho ![]() (Tia
(Tia ![]() khác phía với
khác phía với ![]() đối với
đối với ![]() ). Gọi
). Gọi ![]() là giao điểm của
là giao điểm của ![]() và
và ![]() . Khi đó
. Khi đó ![]() bằng:
bằng:
Hình vẽ minh họa
Xét tam giác ABD và tam giác CID ta có
Xét tam giác ABD và tam giác AIC ta có:
Từ (*) và (**) suy ra
Cho biết tam giác ABC có hai đường cao AD và BE cắt nhau tại H.
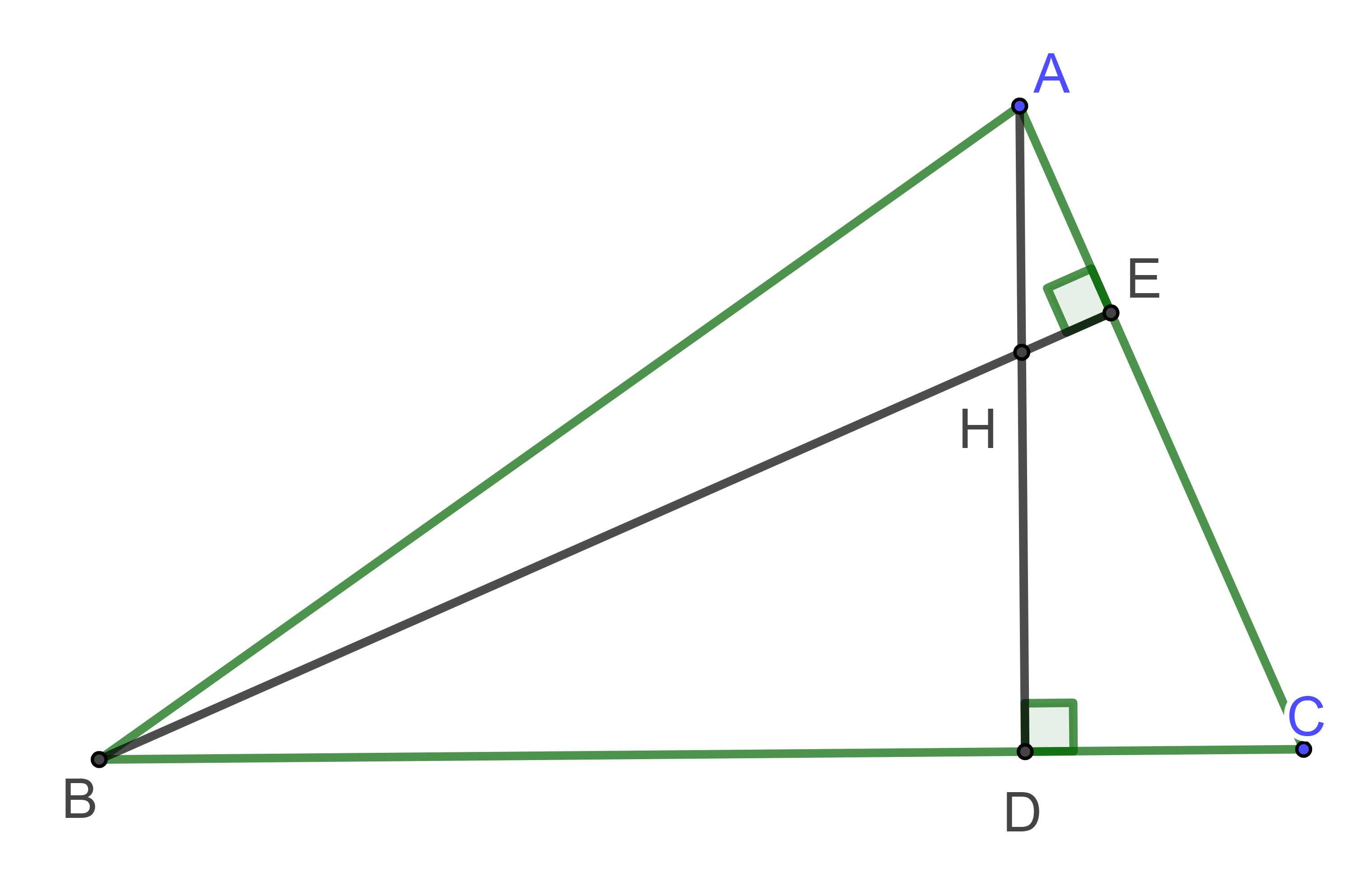
Trong hình có số cặp tam giác đồng dạng với nhau là:
Xét cặp tam giác BEC và tam giác ADC có:
Góc C chung
Xét cặp tam giác AHE và tam giác BHD có:
Xét cặp tam giác AHE và tam giác ACD có:
Góc chung
Xét cặp tam giác AHE và tam giác BCE có:
Xét cặp tam giác BHD và tam giác BEC có:
Góc chung
Xét cặp tam giác BHD và tam giác ADC có:
Vậy có 6 cặp tam giác đồng dạng với nhau.
Tìm khẳng định đúng trong các khẳng định dưới đây?
Hai tam giác bằng nhau có các cặp góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên chúng đồng dạng theo tỉ số 1
=> "Hai tam giác bằng nhau thì đồng dạng" đúng và "Hai tam giác bằng nhau thì không đồng dạng" sai
Hai tam giác đồng dạng thì chưa chắc bằng nhau, nó chỉ bằng nhau khi tỉ số đồng dạng bằng 1
=> "Hai tam giác đồng dạng thì bằng nhau" sai.
Hai tam giác vuông chưa chắc đồng dạng
=> "Hai tam giác vuông luôn đồng dạng với nhau" sai.
Cho tam giác ![]() , kẻ đường phân giác
, kẻ đường phân giác ![]() . Biết
. Biết ![]() . Tính độ dài cạnh
. Tính độ dài cạnh ![]() .
.
Hình vẽ minh họa
Do BD là tia phân giác tam giác ABC nên
Mà nên
.
Vẽ đường phân giác CE của tam giác CBD (E thuộc BD).
(vì BD là phân giác góc
)
(EC là phân giác góc
)
(tam giác ABC cân tại A)
=> Tam giác ECB cân tại E
Đặt ta có
. Xét tam giác CED và tam giác BCD ta có:
Góc chung
Cho tam giác ![]() . Kẻ đường phân giác
. Kẻ đường phân giác ![]() . Kẻ tia
. Kẻ tia ![]() sao cho
sao cho ![]() (Tia
(Tia ![]() khác phía với
khác phía với ![]() đối với
đối với ![]() ). Gọi I là giao điểm của AD và Cx. Tính tích
). Gọi I là giao điểm của AD và Cx. Tính tích ![]() biết
biết ![]() .
.
Hình vẽ minh họa
Xét tam giác ABD và tam giác CID ta có
Hình thang ![]() có
có ![]() đường chéo BD vuông góc với cạnh BC tại B và
đường chéo BD vuông góc với cạnh BC tại B và ![]() ,
, ![]() . Hãy tính độ dài cạnh DC.
. Hãy tính độ dài cạnh DC.
Hình vẽ minh họa
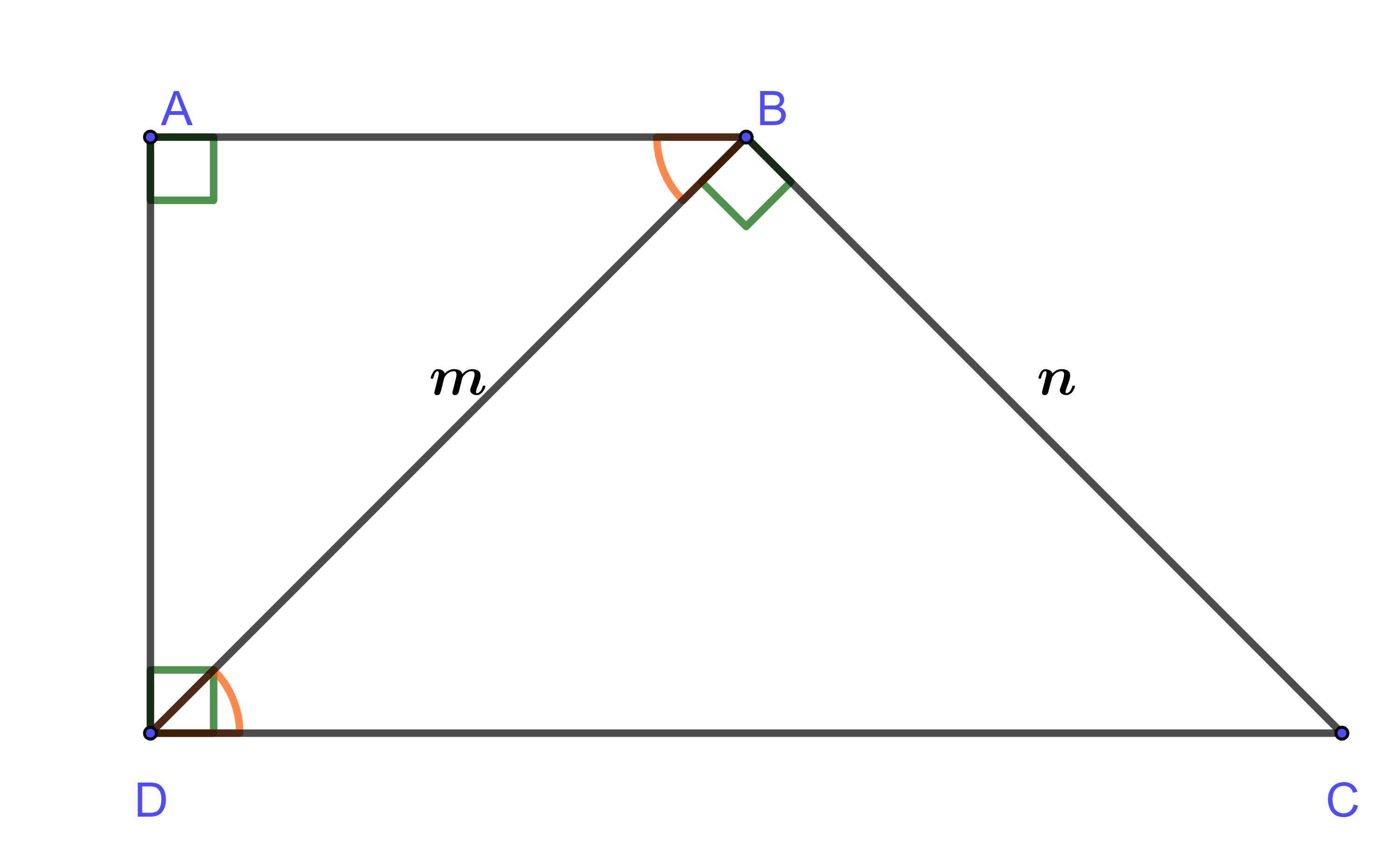
Ta có: ABCD là hình thang vuông tại A và D và nên ta có:
Xét tam giác vuông DBC, theo định lí Pythagore, ta có:
Từ hệ thức (*) ta suy ra:
Thay ta được
Hãy tính độ dài các đoạn thẳng CD trong hình vẽ (làm tròn đến chữ số thập phân thứ nhất)
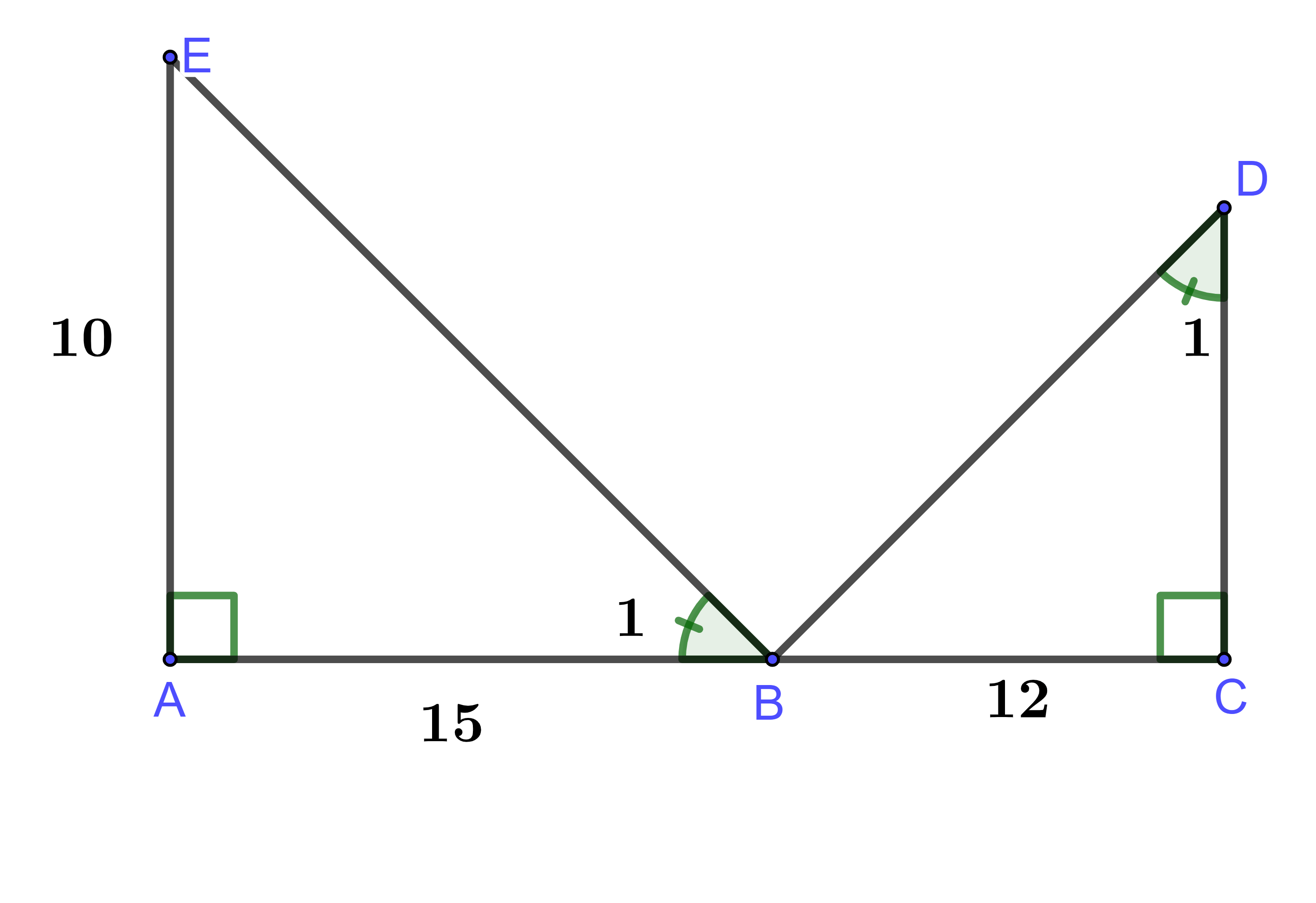
Ta có:
