Cho hình thoi ![]() cạnh
cạnh ![]() có
có ![]() . Đường thẳng d cắt 2 cạnh AB, BC lần lượt tại M, N sao cho
. Đường thẳng d cắt 2 cạnh AB, BC lần lượt tại M, N sao cho ![]() . Tam giác
. Tam giác ![]() là tam giác gì?
là tam giác gì?
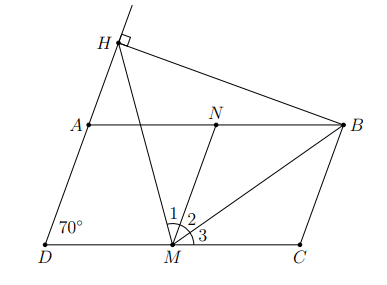
Hình vẽ minh họa:
Theo đề: suy ra
Tam giác đều nên
Xét hai tam giác và
, có:
Do đó
Từ đó
(Vì tam giác
đều)
Tam giác có
và góc
.
Vậy tam giác đều.