Xác định giá trị của x trong hình vẽ, biết ![]()
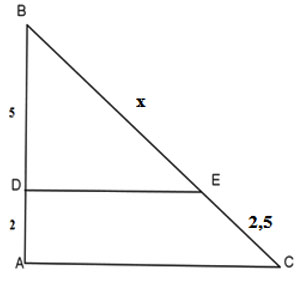
Theo bài ra ta có: , áp dụng định lí Thales ta có:
Xác định giá trị của x trong hình vẽ, biết ![]()

Theo bài ra ta có: , áp dụng định lí Thales ta có:
Cho tam giác ABC có AB = 9cm, lấy điểm D thuộc cạnh AB sao cho AD = 6cm. Kẻ DE song song với BC (E thuộc AC), kẻ EF song song với CD (F thuộc AB). Tính độ dài AF.
Hình vẽ minh họa
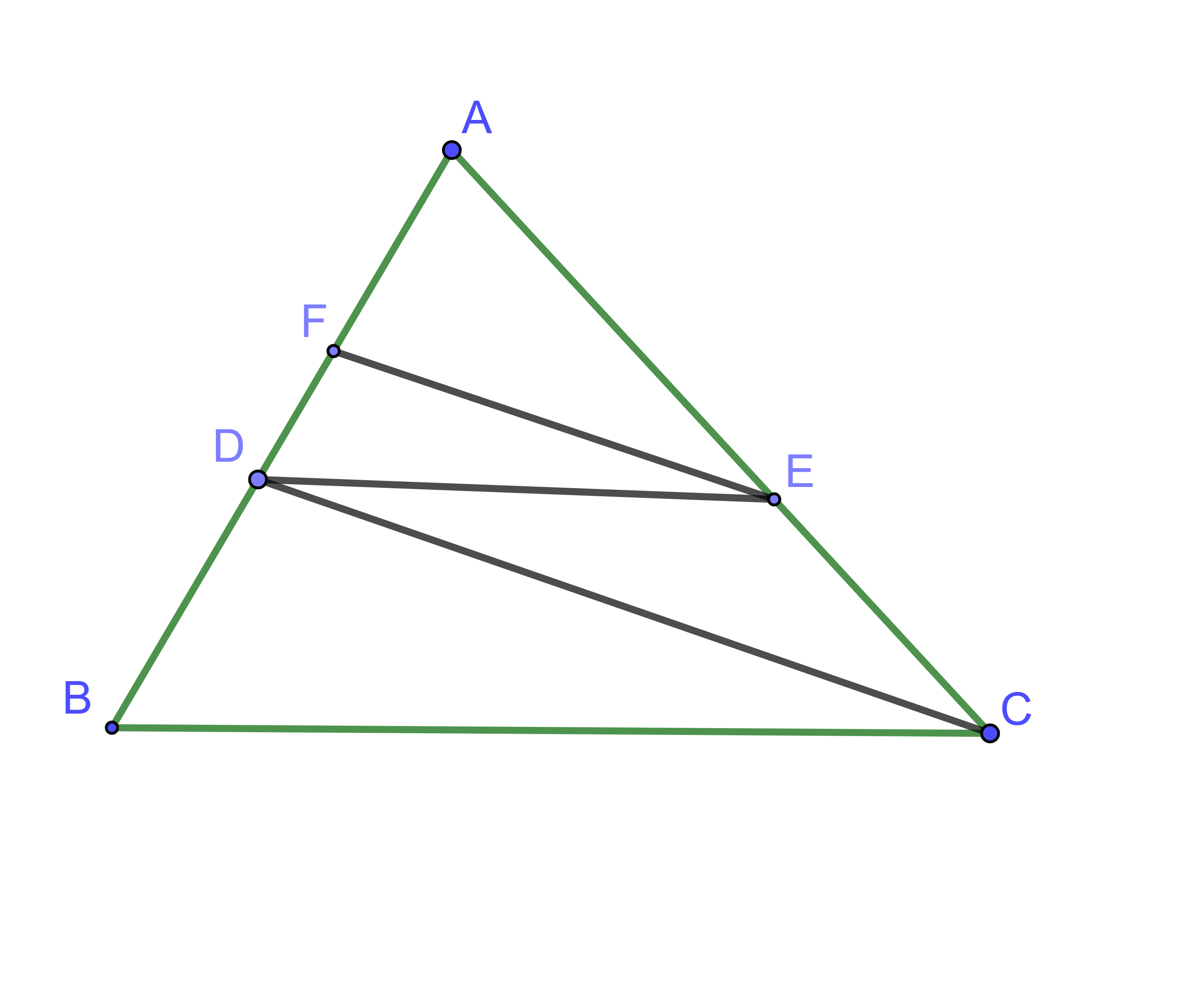
Với EF // CD, áp dụng định lý Thales ta có:
Với DE // BC, áp dụng định lý Thales ta có:
Cho hình vẽ:
Giá trị biểu thức ![]() là:
là:
Áp dụng định lý Pythagore cho tam giác vuông , ta có:
Lại có:
(Theo định lý từ vuông góc đến song song)
Áp dụng định lý Thales, ta có:
Vậy
Cho tam giác ![]() có
có ![]() . Lần lượt lấy trên cạnh
. Lần lượt lấy trên cạnh ![]() các điểm
các điểm ![]() và
và ![]() sao cho
sao cho ![]() và
và ![]() . Khi đó độ dài cạnh
. Khi đó độ dài cạnh ![]() là: 12cm
là: 12cm
Cho tam giác có
. Lần lượt lấy trên cạnh
các điểm
và
sao cho
và
. Khi đó độ dài cạnh
là: 12cm
Hình vẽ minh họa
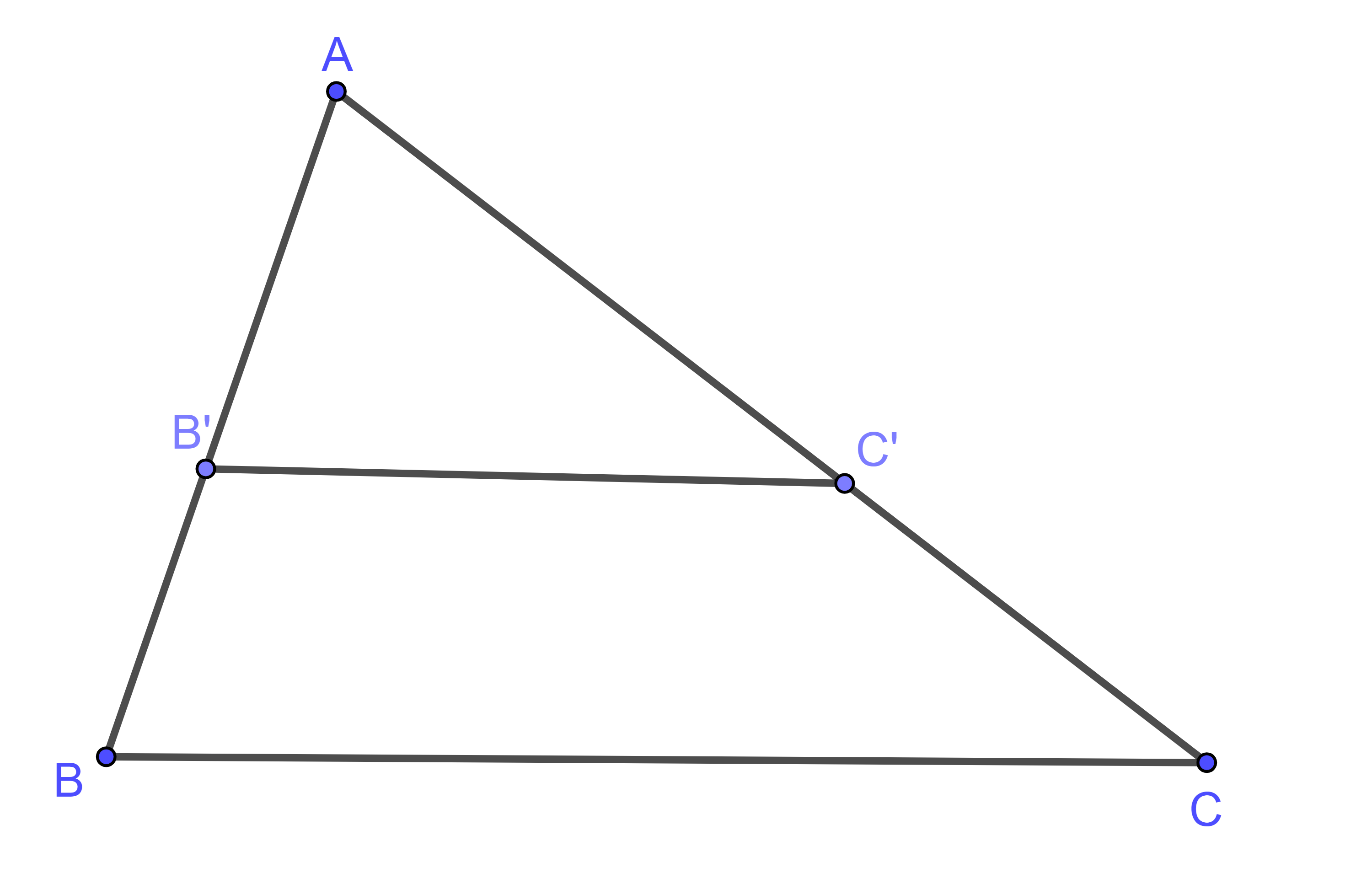
Ta có:
Áp dụng hệ quả của định lí Thales ta có:
Quan sát hình vẽ sau:
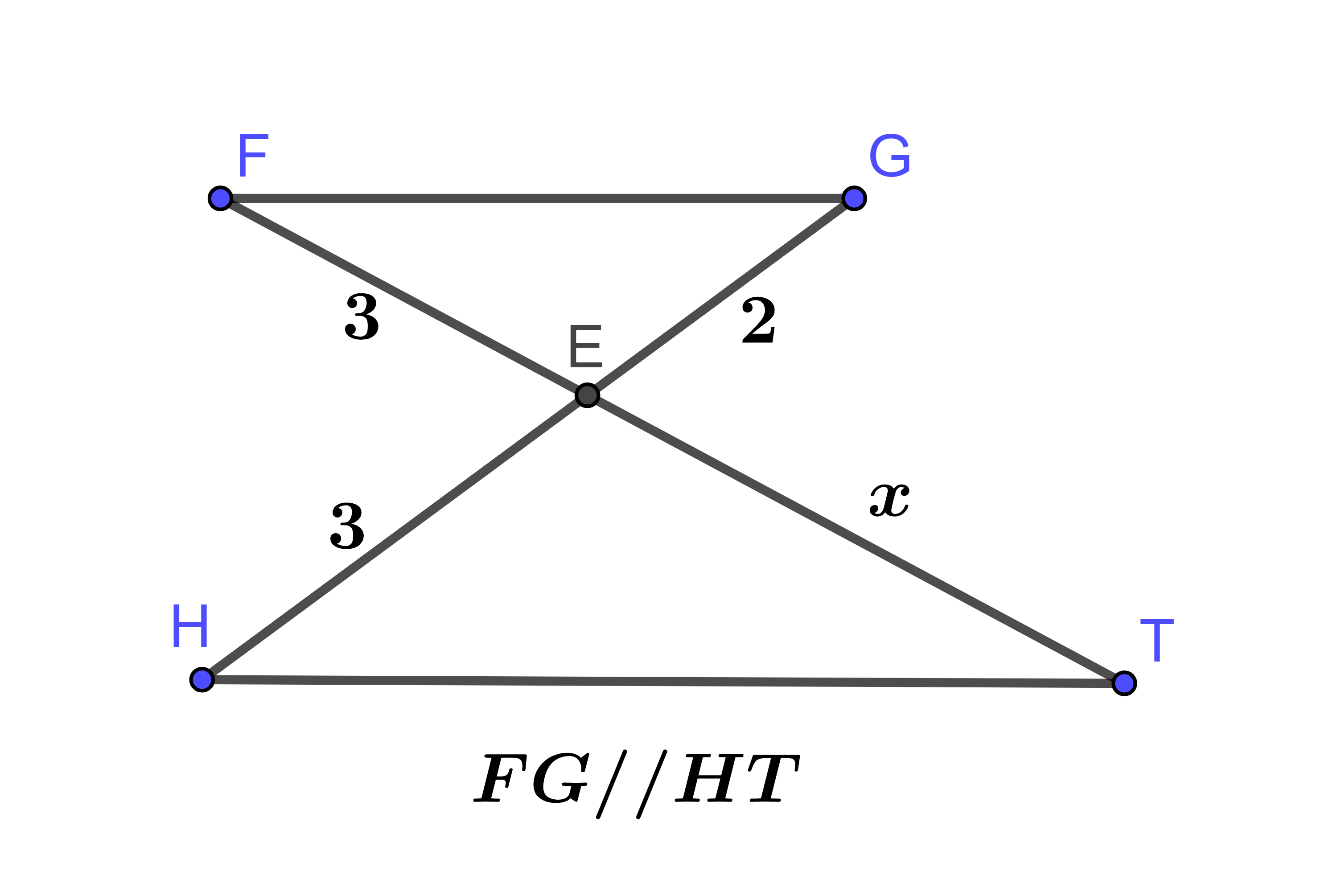
Giá trị của x là:
Áp dụng hệ quả của định lí Thales với ta có:
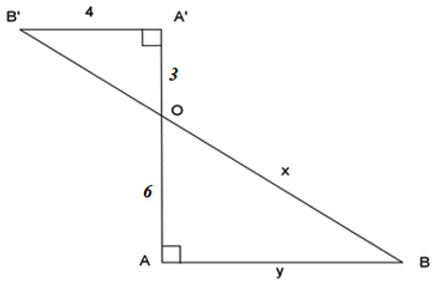
Tình giá trị y trong hình vẽ sau:
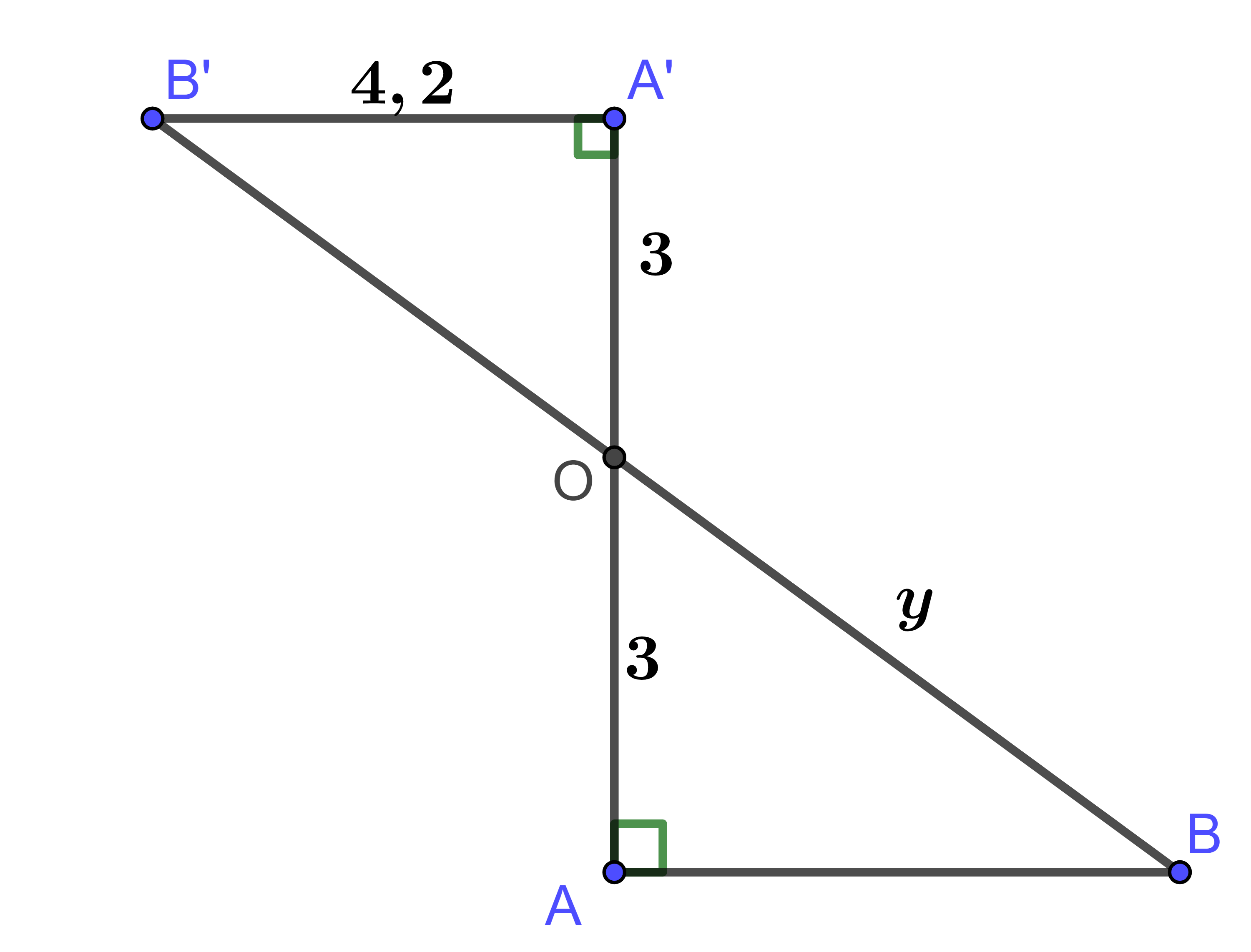
Ta có: vì cùng vuông góc
Áp dụng hệ quả của định lí Thales ta có:
Áp dụng định lí Pythagore trong tam giác OAB ta có:
Cho hình vẽ và tìm giá trị x
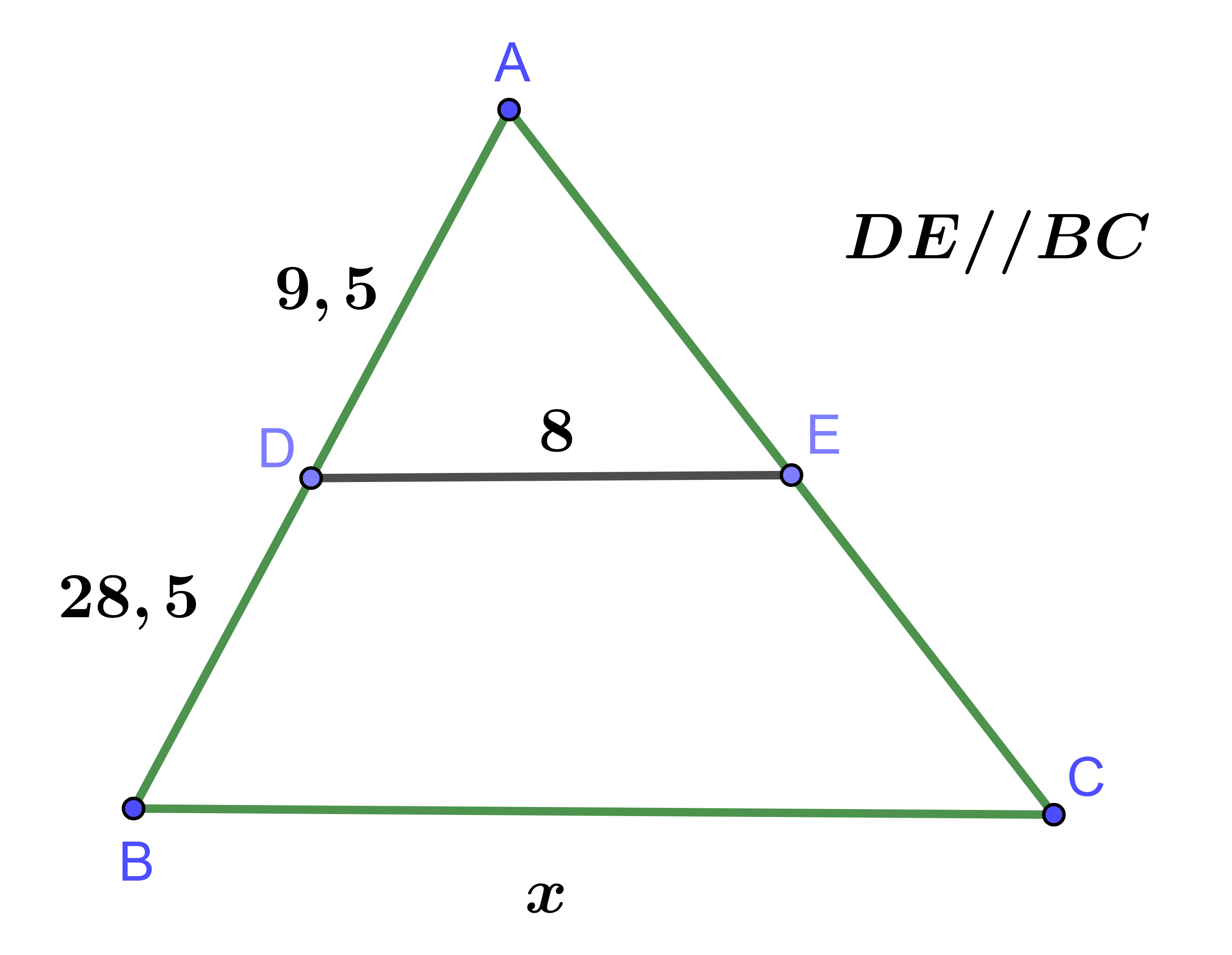
Ta có:
Áp dụng hệ quả của định lí Thales ta có:
Tình giá trị của x trong hình vẽ, biết ED ⊥ AB, AC ⊥ AB
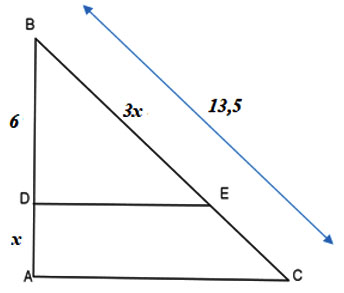
Ta có:
(từ vuông góc đến song song)
Áp dụng định lý Thales, ta có:
Vậy x = 3 thỏa mãn.
Cho hình bên, biết DE // AC

Tính giá trị của x - 1
Theo bài ra ta có: , áp dụng định lí Thales ta có:
Vậy x - 1 = 5,25
Cho hình thang ![]() có
có ![]() . Điểm E thuộc cạnh AD sao cho
. Điểm E thuộc cạnh AD sao cho ![]() Qua E kẻ đường thẳng song song với CD, cắt BC ở F. Tính độ dài BF.
Qua E kẻ đường thẳng song song với CD, cắt BC ở F. Tính độ dài BF.
Hình vẽ minh họa

Gọi I là giao điểm của AC và EF.
Xét tam giác ACB có IF // AB nên theo định lý Thales ta có:
Cho hình vẽ:
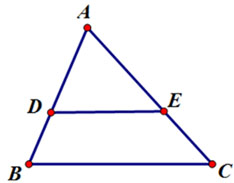
Trong đó ![]() . Độ dài AB bằng:
. Độ dài AB bằng:
Ta có: , theo định lý Thales ta có:
Cho hình thang ![]() có O là giao điểm của hai đường chéo. Đường thẳng qua O song song hai đáy và cắt AD, BC lần lượt tại E và F. Tính tỉ số
có O là giao điểm của hai đường chéo. Đường thẳng qua O song song hai đáy và cắt AD, BC lần lượt tại E và F. Tính tỉ số ![]() .
.
Hình vẽ minh họa
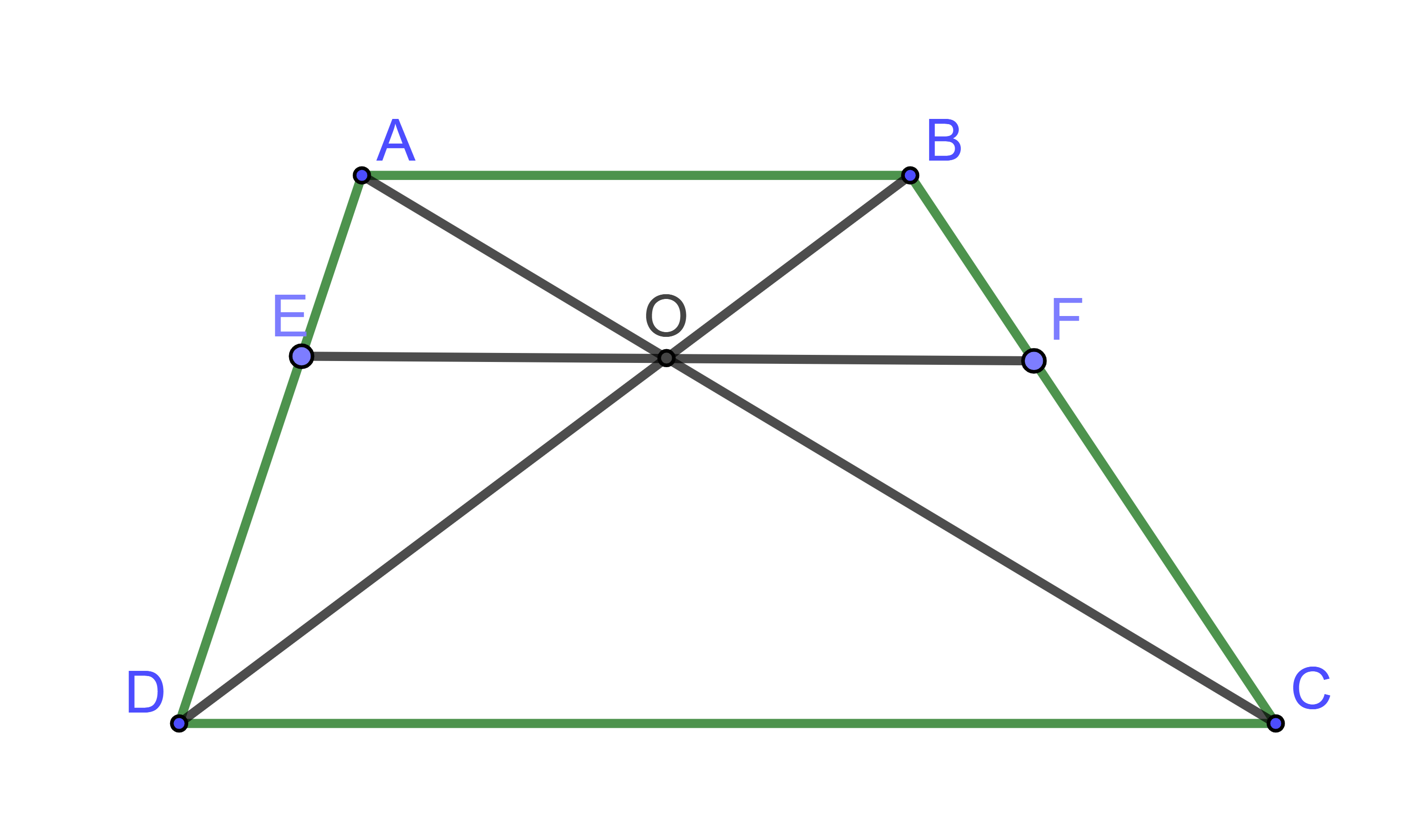
Áp dụng hệ quả của định lí Thales cho và
ta được:
Vậy
Trong tam giác ABC kẻ đường thẳng song song với BC cắt các cạnh AB và AC theo thứ tự tại D và E. Qua E kẻ đường thẳng song song với CD, cắt AB ở F. Tính độ dài AD, biết ![]() .
.
Hình vẽ minh họa

Với EF // CD, áp dụng định lý Thales ta có:
Với DE // BC, áp dụng định lý Thales ta có:
Cho hình thang ![]() ,
, ![]() là giao điểm của hai đường chéo. Tính diện tích tam giác
là giao điểm của hai đường chéo. Tính diện tích tam giác ![]() , biết hình thang có diện tích
, biết hình thang có diện tích ![]() ,
, ![]() .
.
Hình vẽ minh họa
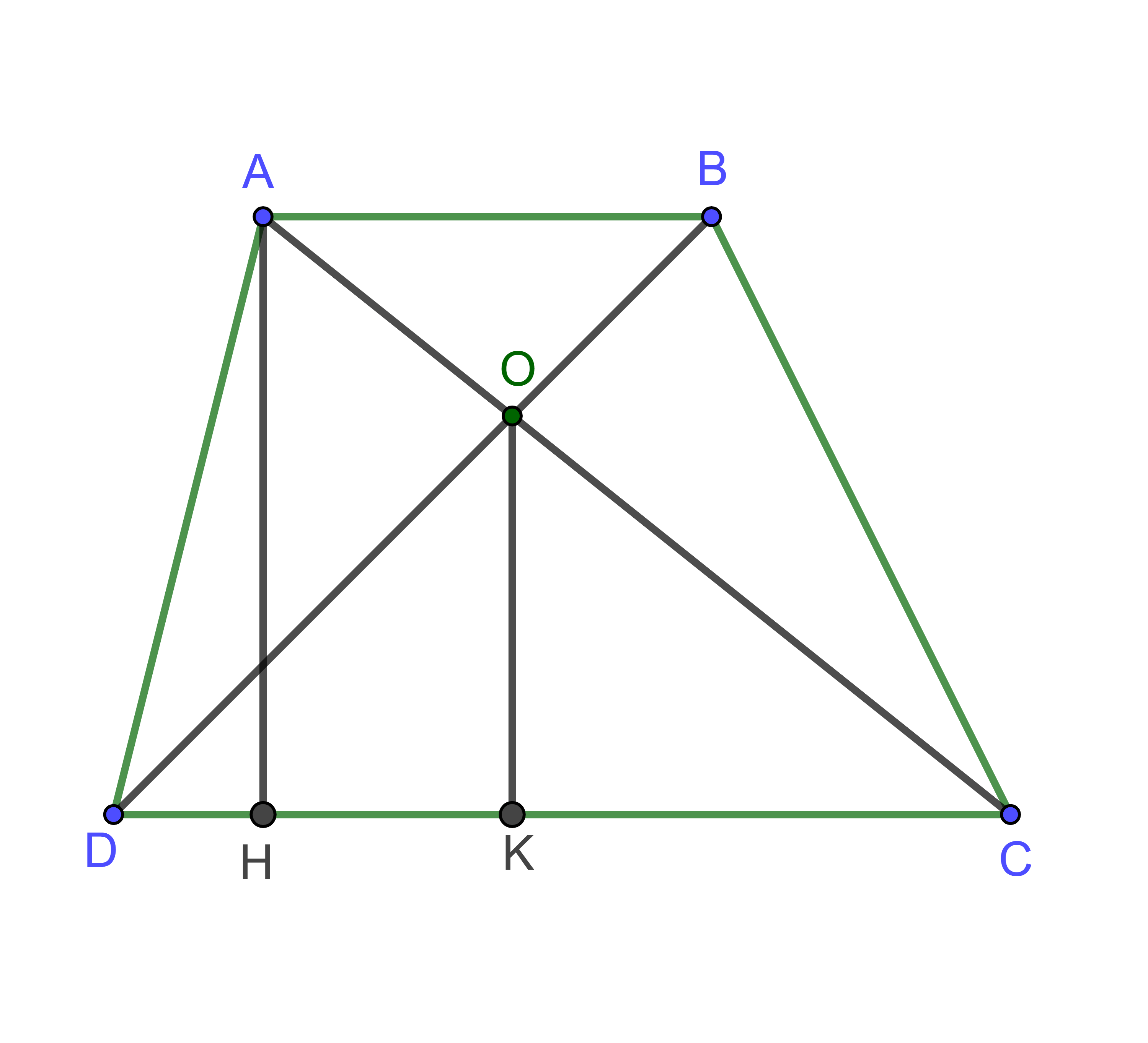
Kẻ tại H, K
Chiều cao của hình thang:
Vì (do ABCD là hình thang) nên theo định lý Thales ta có
Vì (chứng minh trên) nên theo định lý Thales cho tam giác AHC ta có:
Vậy diện tích tam giác OCD là:
Tìm giá trị của x trên hình vẽ.
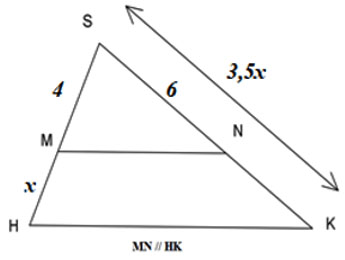
Ta có: , áp dụng định lí Thales ta có:
