Cho hình bình hành ![]() , gọi
, gọi ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() và
và ![]() . Khi đó:
. Khi đó:
Hình vẽ minh họa
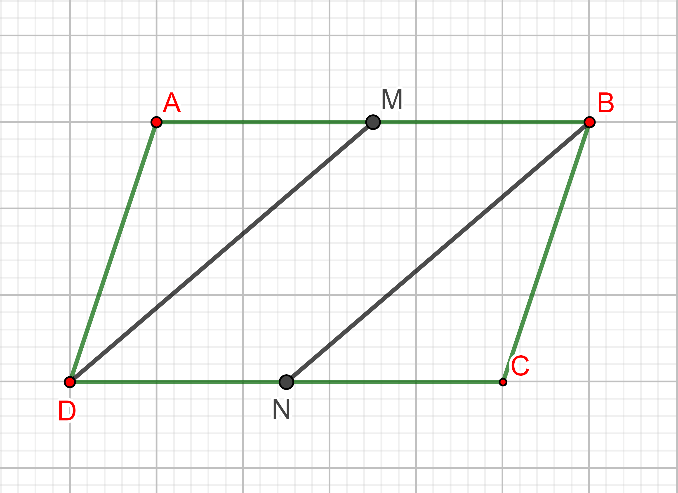
Vì là hình bình hành nên
Xét tứ giác có:
(do
) nên
là hình bình hành.
Từ đó: (tính chất hình bình hành)
Cho hình bình hành ![]() , gọi
, gọi ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() và
và ![]() . Khi đó:
. Khi đó:
Hình vẽ minh họa

Vì là hình bình hành nên
Xét tứ giác có:
(do
) nên
là hình bình hành.
Từ đó: (tính chất hình bình hành)
Hoàn thành câu sau: “Tứ giác có hai đường chéo … thì tứ giác đó là hình bình hành”.
Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Chọn khẳng định sai trong các khẳng định dưới đây?
Dấu hiệu nhận biết:
Tứ giác có các cạnh đối song song là hình bình hành nên A đúng
Tứ giác có các cạnh đối bằng nhau là hình bình hành nên D đúng
Tứ giác có các góc đối bằng nhau là hình bình hành nên D đúng
Nhận thấy hình thang có hai góc kề một đáy bằng nhau là hình thang cân nên khẳng định sai là: “Hình thang có hai góc kề một đáy bằng nhau là hình bình hành”
Cho tứ giác ![]() có
có ![]() . Tìm điều kiện để
. Tìm điều kiện để ![]() có chu vi nhỏ nhất.
có chu vi nhỏ nhất.
Hình vẽ minh họa
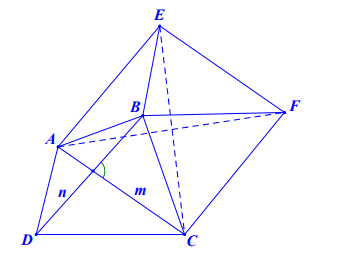
Vẽ hình bình hành và
Khi đó:
Như vậy hình bình hành hoàn toàn được xác định, do đó hai đường chéo
và
không đổi.
Dễ thấy tứ giác BFCD là hình bình hành
Chu vi tứ giác là:
Dấu bằng xảy ra khi và chỉ khi thẳng hàng và
thẳng hàng
Vậy để chu vi đạt giá trị nhỏ nhất thì
là hình bình hành.
Cho hình bình hành ![]() . Hỏi hai góc kề nhau của hình bình hành không thể có số đo nào sau đây?
. Hỏi hai góc kề nhau của hình bình hành không thể có số đo nào sau đây?
Trong hình bình hành có các góc đối nhau và tổng các góc trong hình bình hành phải bằng 3600.
Mà
Vậy hai góc kề nhau của hình bình hành không thể là cặp góc .
Cho tam giác ![]() có hai đường trung tuyến
có hai đường trung tuyến ![]() và
và ![]() vuông góc với nhau. Gọi là trung điểm của
vuông góc với nhau. Gọi là trung điểm của ![]() . Chọn khẳng định đúng.
. Chọn khẳng định đúng.
Hình vẽ minh họa
Trên tia ED lấy điểm K sao cho D là trung điểm của EK.
Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
Ta có:
Vậy tứ giác DKFB là hình bình hành
Mặt khác, nên
Do đó ∆KAF vuông tại A
Cho hình bình hành ![]() . Chọn khẳng định sai.
. Chọn khẳng định sai.
Trong hình bình hành:
Hình bình hành có các cạnh đối song song
Các cạnh đối bằng nhau
Hai đường chéo cắt nhau tại trung điểm của mỗi đường
Vậy khẳng định sai là: “”
Tứ giác ![]() là hình bình hành nếu:
là hình bình hành nếu:
Tứ giác là hình bình hành nếu
Cho hình bình hành ![]() . Vẽ ra ngoài hình bình hành các tam giác
. Vẽ ra ngoài hình bình hành các tam giác ![]() vuông cân tại , tam giác
vuông cân tại , tam giác ![]() vuông cân tại
vuông cân tại ![]() . Tam giác
. Tam giác ![]() là tam giác gì?
là tam giác gì?
Hình vẽ minh họa
Đặt
Xét tam giác và tam giác
có:
Do đó
Kéo dài cắt
tại
ta có:
Xét tam giác MDH có:
Hay
Vậy tam giác là tam giác vuông cân.
Vẽ ra phía ngoài tam giác ABC các tam giác ABD vuông cân tại B, ACE vuông cân tại C. Gọi M là trung điểm của DE. Hãy xác định dạng của tam giác BMC.
Hình vẽ minh họa
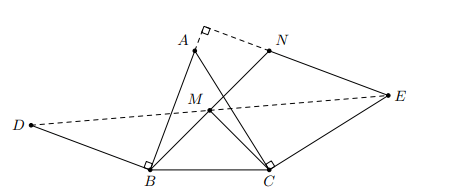
Trên tia đối của tia MB lấy , khi đó tứ giác BDNE là hình bình hành, suy ra
và
Ta lại có .
Từ đó ta có
Suy ra và
.
Do đó tam giác vuông cân, suy ra tam giác
vuông cân tại M.
Cho tam giác nhọn ![]() . Vẽ ra phía ngoài của tam giác này các tam giác
. Vẽ ra phía ngoài của tam giác này các tam giác ![]() và tam giác
và tam giác ![]() vuông cân tại
vuông cân tại ![]() . Gọi
. Gọi ![]() là trung điểm của
là trung điểm của ![]() . Khi đó số đo góc
. Khi đó số đo góc ![]() bằng bao nhiêu?
bằng bao nhiêu?
Hình vẽ minh họa
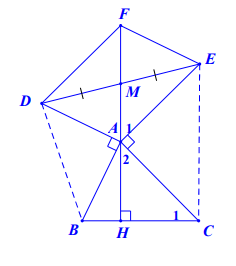
Vẽ hình bình hành . Khi đó
đi qua
. Gọi là giao điểm của
với
.
Ta có:
Mà
Suy ra
Ta có:
Cho tam giác ![]() , các đường cao
, các đường cao ![]() và
và ![]() cắt nhau tại
cắt nhau tại ![]() . Đường thẳng qua
. Đường thẳng qua ![]() vuông góc với
vuông góc với ![]() và đường thẳng qua
và đường thẳng qua ![]() vuông góc với
vuông góc với ![]() cắt nhau tại
cắt nhau tại ![]() . Gọi
. Gọi ![]() là trung điểm của
là trung điểm của ![]() . Cho biết tứ giác
. Cho biết tứ giác ![]() là hình gì?
là hình gì?
Hình vẽ minh họa
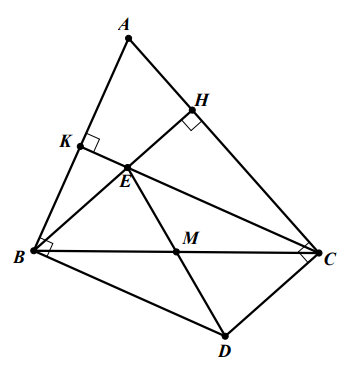
Ta có:
Lại có:
Từ (1) và (2) suy ra là hình bình hành
Cho tam giác ![]() , các đường cao
, các đường cao ![]() và
và ![]() cắt nhau tại
cắt nhau tại ![]() . Đường thẳng qua vuông góc với
. Đường thẳng qua vuông góc với ![]() và đường thẳng qua
và đường thẳng qua ![]() vuông góc với
vuông góc với ![]() cắt nhau tại
cắt nhau tại ![]() . Gọi
. Gọi ![]() là trung điểm của
là trung điểm của ![]() . Tính tổng số đo hai góc
. Tính tổng số đo hai góc ![]() .
.
Hình vẽ minh họa
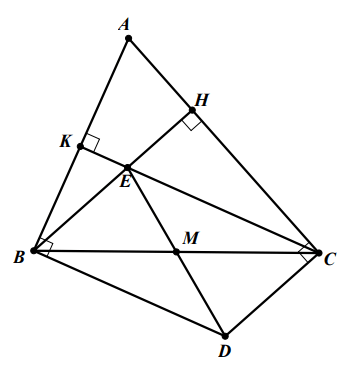
Ta có:
Lại có:
Từ (1) và (2) suy ra BDCE là hình bình hành.
Mặt khác
Từ (3) và (4) suy ra
Tính độ dài đường trung tuyến AM của tam giác ABC có ![]() ,
, ![]() .
.
Vẽ điểm E sao cho M là trung điểm của AE.
Tứ giác ABEC là hình bình hành
Kẻ . Tam giác vuông ABH có
Suy ra
Trong tam giác vuông ABH ta có
Trong tam giác vuông AHE ta có
Cho tam giác ![]() cân tại
cân tại ![]() . Lấy điểm
. Lấy điểm ![]() trên cạnh
trên cạnh ![]() , điểm
, điểm ![]() trên cạnh
trên cạnh ![]() sao cho
sao cho ![]() . Gọi
. Gọi ![]() là trung điểm của
là trung điểm của ![]() ,
, ![]() là giao điểm của
là giao điểm của ![]() và
và ![]() . Tứ giác
. Tứ giác ![]() là hình gì?
là hình gì?
Hình vẽ minh họa
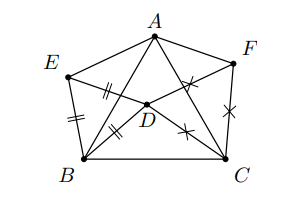
Xét hai tam giác DBC và tam giác EBA có:
Do đó .
Chứng minh tương tự có
Từ (1) và (2) => AEDF là hình bình hành.
