Cho hình thang cân ![]() có
có ![]() . Kẻ các đường cao
. Kẻ các đường cao ![]() và
và ![]() . Tính độ dài cạnh
. Tính độ dài cạnh ![]() .
.
Dễ dàng chứng minh được:
Ta có:
Do
Áp dụng định lí Pythagore cho tam giác BCH vuông tại H ta có:
Cho hình thang cân ![]() có
có ![]() . Kẻ các đường cao
. Kẻ các đường cao ![]() và
và ![]() . Tính độ dài cạnh
. Tính độ dài cạnh ![]() .
.
Dễ dàng chứng minh được:
Ta có:
Do
Áp dụng định lí Pythagore cho tam giác BCH vuông tại H ta có:
Hình thang ![]() có
có ![]() . Số đo các góc của hình thang:
. Số đo các góc của hình thang:
Hình thang có
. Số đo các góc của hình thang:
Ta có: ABCD là hình thang suy ra:
Cho hình thang cân ![]() có
có ![]() và
và ![]() là tia phân giác góc
là tia phân giác góc ![]() . Tính chu vi hình thang
. Tính chu vi hình thang ![]() .
.
Hình vẽ minh họa
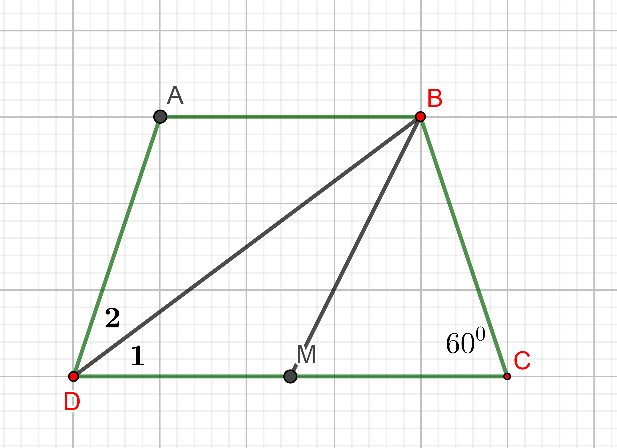
Ta có:
BD là phân giác góc D
Suy ra vậy tam giác ABD cân tại A
Lấy M là trung điểm cạnh DC
Mà tam giác DBC vuông tại B
Xét tam giác BMC cân tại M có
=> Tam giác BMC đều
Chu vi hình thang là:
Hình thang ![]() có
có ![]() . Tính số đo góc
. Tính số đo góc ![]() ?
?
Ta có: ABCD là hình thang suy ra:
Cho tam giác ![]() cân tại
cân tại ![]() , điểm
, điểm ![]() thuộc đường cao
thuộc đường cao ![]() , là giao điểm của
, là giao điểm của ![]() và
và ![]() ,
, ![]() là giao điểm của
là giao điểm của ![]() và
và ![]() . Xác định vị trí điểm
. Xác định vị trí điểm ![]() sao cho
sao cho ![]() ?
?
Hình vẽ minh họa
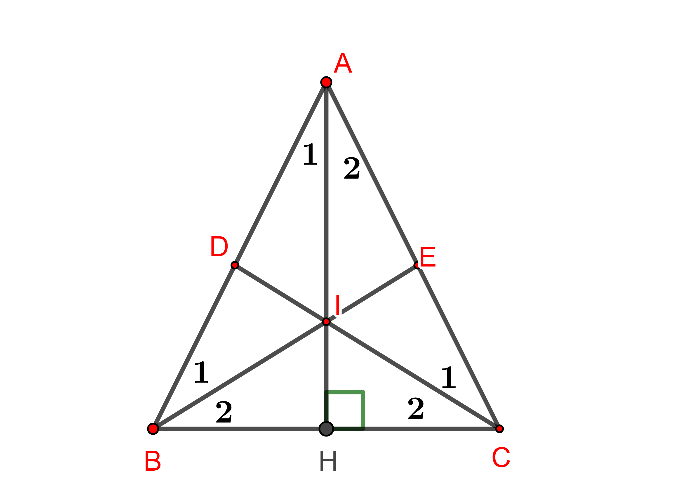
Chứng minh được
=> Tam giác AED cân tại A
Mặt khác tam giác ABC cân tại A
Suy ra tứ giác BDEC là hình thang cân
Ta có:
Để thì tam giác BDE cân tại E
Tương tự ta phải có:
Vậy lần lượt là phân giác góc
và góc
.
Vậy I là giao điểm ba đường phân giác tam giác ABC.
Cho hình thang cân ![]() có
có ![]() . Xác định số đo các góc A và C của hình thang
. Xác định số đo các góc A và C của hình thang ![]() .
.
Hình vẽ minh họa
Ta có:
Dùng góc làm trung gian để chứng minh
Chứng minh tương tự ta được . Ta còn có
Xét tam giác BDC vuông tại B ta có:
Một hình thang cân có đáy nhỏ bằng cạnh bên và góc kề với đáy bằng 600. Tính chu vi hình thang cân. Biết chiều cao hình thang cân bằng ![]() .
.
Hình vẽ minh họa
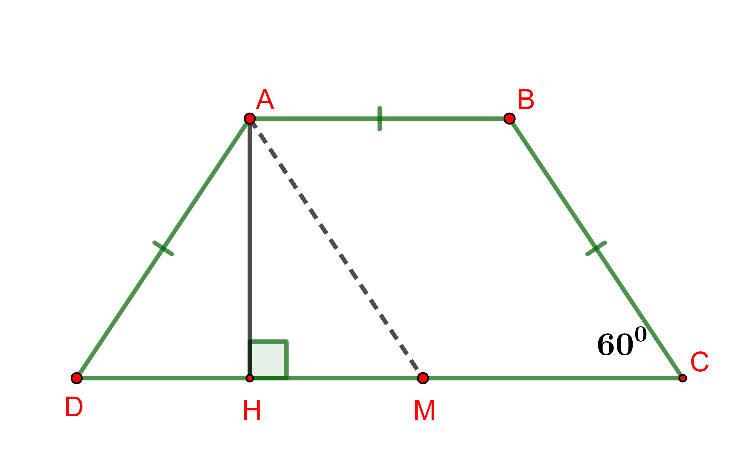
Ta đặt
Vẽ , ta được
và
Ta lại có tam giác cân, nên là tam giác đều, suy ra:
.
Vẽ thì
là đường cao của hình thang cân, cũng là đường cao của tam giác đều:
vì
Do đó chu vi của hình thang cân là:
Cho hình thang ABCD có AB // CD, biết rằng ![]() . Khi đó số đo các góc hình thang là:
. Khi đó số đo các góc hình thang là:
Cho hình thang ABCD có AB // CD, biết rằng . Khi đó số đo các góc hình thang là:
Ta có: ABCD là hình thang nên
Ta có: ABCD là hình thang nên
Cho hình thang cân ![]() có
có ![]() . Tính số đo góc
. Tính số đo góc ![]() .
.
Ta có:
Cho hình thang cân ![]() có
có ![]() . Tính diện tích hình thang cân ABCD, biết
. Tính diện tích hình thang cân ABCD, biết ![]() .
.
Hình vẽ minh họa
Hạ
Ta có:
Diện tích hình thang cân ABCD là
Hình thang cân ![]() có
có ![]() và
và ![]() là hai đường cao của hình thang. Biết
là hai đường cao của hình thang. Biết ![]() . Tính diện tích hình thang
. Tính diện tích hình thang ![]() .
.
Hình vẽ minh họa
Ta chứng minh được:
Hình thang có
Vậy diện tích hình thang ABCD là:
Cho hình thang cân ABCD có ![]() thì:
thì:
Trong hình thang cân hai góc ở đáy bằng nhau
Cho hình thang như hình vẽ. Biết diện tích tam giác AOD là 10cm2 và diện tích tam giác OCD là 20cm2. Tính diện tích hình thang ABCD.

Ta có:
Xét hai tam giác ADC và BDC, ta thấy hai tam giác đều có chiều cao bằng nhau và chung đáy DC nên diện tích tam giác ADC bằng diện tích tam giác BDC
Do
Tam giác AOD và tam giác DOC đều có chung chiều cao hạ từ D;
Suy ra .
Tam giác ABO và tam giác BOC có chung chiều cao hạ từ B, có đáy OC gấp 2 lần đáy AO, suy ra
Do đó:
Ta có
Cho hình thang ![]() biết
biết ![]() . Tính đường cao
. Tính đường cao ![]() .
.
Hình vẽ minh họa
Ta tính được
Vận dụng nhận xét hình thang có hai cạnh bên song song thì hai cạnh đáy bằng nhau, để tính được
Chứng minh tam giác vuông cân tại
, nên
.
Cho hình thang cân ![]() có đường chéo BD vuông góc với cạnh bên BC và đồng thời BD là tia phân giác góc
có đường chéo BD vuông góc với cạnh bên BC và đồng thời BD là tia phân giác góc ![]() . Tính số đo các góc B và góc D hình thang cân ABCD.
. Tính số đo các góc B và góc D hình thang cân ABCD.
Tam giác DBC vuông:
