Cho tam giác MNP như hình vẽ:

Biết MA là phân giác ngoài của góc M và ![]() . Chọn đáp án đúng.
. Chọn đáp án đúng.
Theo tính chất đường phân giác của tam giác ta có:
Cho tam giác MNP như hình vẽ:

Biết MA là phân giác ngoài của góc M và ![]() . Chọn đáp án đúng.
. Chọn đáp án đúng.
Theo tính chất đường phân giác của tam giác ta có:
Quan sát hình vẽ sau:

Chọn đáp án chưa chính xác?
Áp dụng tính chất đường phân giác cho tam giác EFG, phân giác GH ta có:
Lại có: (theo tính chất dãy tỉ số bằng nhau)
Vậy đáp án sai là:
Tìm x trong hình vẽ:

Áp dụng tính chất tính chất đường phân giác trong tam giác ta có:
Cho ![]() , AD là phân giác trong của góc A, D thuộc cạnh BC. Độ dài đoạn thẳng BD là: 8cm
, AD là phân giác trong của góc A, D thuộc cạnh BC. Độ dài đoạn thẳng BD là: 8cm
Cho , AD là phân giác trong của góc A, D thuộc cạnh BC. Độ dài đoạn thẳng BD là: 8cm
Hình vẽ minh họa:
Ta có AD là phân giác trong của tam giác ABC
Mà
Tính tỉ lệ độ dài hai cạnh x và y trong hình vẽ sau:

Ta có: AD là phân giác trong của tam giác ABC
Cho hình vẽ:

Biết AD là phân giác góc A. Chọn khẳng định đúng?
Ta có: AD là phân giác góc A nên ta có:
(tính chất đường phân giác của tam giác)
Tính độ dài x và y trong hình vẽ sau:

Giá trị của x là là: 75/7
Giá trị của y là: 100/7
(Kết quả được ghi dưới dạng phân số tối giản a/b)
Tính độ dài x và y trong hình vẽ sau:
Giá trị của x là là: 75/7
Giá trị của y là: 100/7
(Kết quả được ghi dưới dạng phân số tối giản a/b)
Ta có: AD là phân giác trong của tam giác ABC
Áp dụng tính chất đường phân giác trong tam giác ta có:
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Quan sát hình vẽ sau:

Tỉ số ![]() 7/15
7/15
(Ghi đáp án dưới dạng phân số tối giản a/b).
Quan sát hình vẽ sau:
Tỉ số 7/15
(Ghi đáp án dưới dạng phân số tối giản a/b).
Ta có AD là phân giác góc nên ta có:
Cho tam giác ABC có AE là phân giác ngoài góc A. Đẳng thức nào sau đây đúng?
Xét tam giác ABC có AE là phân giác ngoài của góc A thì
Cho tam giác ABC, trung điểm cạnh BC tại điểm I. Kẻ đường phân giác của góc ![]() cắt cạnh AB tại E. Đường phân giác góc
cắt cạnh AB tại E. Đường phân giác góc ![]() cắt cạnh AC tại F. Để tứ giác AEIF là hình vuông thì tam giác ABC là Tam giác vuông cân || Tam giác vuông || Tam giác cân || Tam giác đều
cắt cạnh AC tại F. Để tứ giác AEIF là hình vuông thì tam giác ABC là Tam giác vuông cân || Tam giác vuông || Tam giác cân || Tam giác đều
Cho tam giác ABC, trung điểm cạnh BC tại điểm I. Kẻ đường phân giác của góc cắt cạnh AB tại E. Đường phân giác góc
cắt cạnh AC tại F. Để tứ giác AEIF là hình vuông thì tam giác ABC là Tam giác vuông cân || Tam giác vuông || Tam giác cân || Tam giác đều
Hình vẽ minh họa
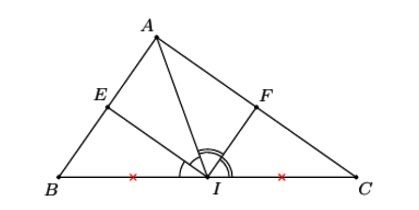
Để tứ giác AEIF là hình vuông thì
Tương đương với tam giác ABC vuông tại A.
AEIF là hình vuông suy ra AI là phân giác góc BAC
Suy ra tam giác ABC có AI là trung tuyến cũng là phân giác do đó tam giác ABC cân tại A
Vậy tam giác ABC vuông cân tại A
Ngược lại khi tam giác ABC vuông cân tại A ta dễ dàng chứng minh được tam giác ABC và tam giác ACI vuông cân tại I, do đó đường phân giác IE và IF là các đường cao.
Suy ra
Tứ giác AEIF có
Suy ra AEIF là hình chữ nhật
Mà tam giác ABC vuông cân nên AI là phân giác góc BAC, hay AI là phân giác góc EAF
Suy ra AEIF là hình vuông.
Vậy để tứ giác AEIF là hình vuông thì tam giác ABC phải vuông cân tại A.
Cho ![]() có
có ![]() . Kẻ đường phân giác trong góc B cắt AC tại E. Tính độ dài cạnh CE biết
. Kẻ đường phân giác trong góc B cắt AC tại E. Tính độ dài cạnh CE biết ![]() .
.
Ta có: BE là phân giác trong của góc B
Áp dụng tính chất đường phân giác trong tam giác ta có:
Cho tam giác ABC có ![]() , đường phân giác trong góc A cắt BC tại M. Từ M kẻ ME song song với AB,
, đường phân giác trong góc A cắt BC tại M. Từ M kẻ ME song song với AB, ![]() . Tính độ dài đoạn ME?
. Tính độ dài đoạn ME?
Giá trị đoạn ME là: 2,4cm
(Ghi đáo án dưới dạng số thập phân).
Cho tam giác ABC có , đường phân giác trong góc A cắt BC tại M. Từ M kẻ ME song song với AB,
. Tính độ dài đoạn ME?
Giá trị đoạn ME là: 2,4cm
(Ghi đáo án dưới dạng số thập phân).
Hình vẽ minh họa
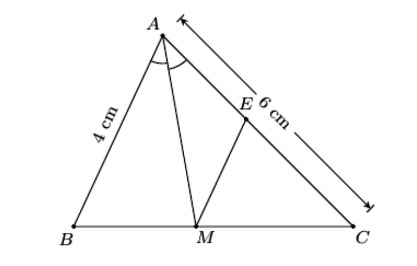
Áp dụng tính chất đường phân giác cho tam giác ABC phân giác AM ta có:
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Áp dụng hệ quả định lí Thales cho tam giác ABC có :
Quan sát hình vẽ:

Giá trị của x là 5,6cm
(Kết quả ghi dưới dạng số thập phân).
Quan sát hình vẽ:
Giá trị của x là 5,6cm
(Kết quả ghi dưới dạng số thập phân).
Ta có: CD là phân giác trong của góc C
Áp dụng tính chất đường phân giác của tam giác ta có:
Cho tam giác ABC cân tại A, đường cao AH. Kẻ đường phân giác trong của góc B cắt AH tại I. Biết ![]() và
và ![]() . Tính chu vi tam giác ABC?
. Tính chu vi tam giác ABC?
Hình vẽ minh họa
Áp dụng tính chất đường phân giác cho tam giác ABH, phân giác BI ta có:
Lại có tam giác ABC cân tại A
=> AH vừa là đường cao, đường trung tuyến, đương phân giác, đường trung trực của tam giác ABC
=> H là trung điểm của BC
Chu vi tam giác ABC là:
Cho tam giác ABC có ![]() và đường phân giác trong AD, D thuộc BC. Hãy xác định tỉ lệ đúng sau đây?
và đường phân giác trong AD, D thuộc BC. Hãy xác định tỉ lệ đúng sau đây?
Áp dụng tính chất đường phân giác của tam giác ta có:
