Lớp 8 Toán 8 - Cánh diều

Ôn tập Chương 1 Đa thức nhiều biến

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 15 câu
  • Điểm số bài kiểm tra: 15 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Thông hiểu
    Thực hiện phép tính

    Phép chia x3 + x2 - 4x + 7 cho x2 - 2x + 5 được đa thức dư là ?

    Hướng dẫn:

    Thực hiện phép tính

    Thực hiện phép tính

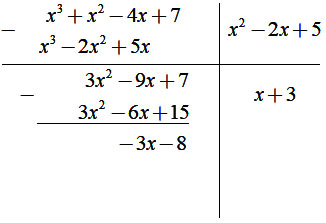
    Vậy phép chia có dư -3x - 8

  • Câu 2: Vận dụng
    Tìm giá trị a

    Phân tích đa thức thành nhân tử ta được

    {x^3} + 7{x^2} + 12x + 4 = \left( {x + 2} ight)\left( {{x^2} + a.x + 2} ight)

    Khi đó giá trị của a là:

    Hướng dẫn:

     Ta có:

    \begin{matrix} {x^3} + 7{x^2} + 12x + 4 \hfill \\ = \left( {{x^3} + 8} ight) + \left( {7{x^2} + 12x - 4} ight) \hfill \\ = \left( {x + 2} ight)\left( {{x^2} - 2x + 4} ight) + \left( {x + 2} ight)\left( {7x - 2} ight) \hfill \\ = \left( {x + 2} ight)\left( {{x^2} - 2x + 4 + 7x - 2} ight) \hfill \\ = \left( {x + 2} ight)\left( {{x^2} + 5x + 2} ight) \hfill \\ \end{matrix}

    Vậy a=5

  • Câu 3: Thông hiểu
    Tìm hệ số thỏa mãn đề bài

    Tìm hệ số x^2 sau khi khai triển biểu thức 

    {\left( {x - 3} ight)^2} + {\left( {2x + 1} ight)^2} + {\left( {{x^2} + 5} ight)^2}

    Hướng dẫn:

     Ta có:

    \begin{matrix} {\left( {x - 3} ight)^2} + {\left( {2x + 1} ight)^2} + {\left( {{x^2} + 5} ight)^2} \hfill \\ = {x^2} - 6x + 9 + 4{x^2} + 4x + 1 + {x^4} + 10{x^2} + 25 \hfill \\ = {x^4} + 15{x^2} - 2x + 35 \hfill \\ \end{matrix}

    Vậy hệ số của x^2 là 15.

  • Câu 4: Vận dụng
    Tính giá trị biểu thức P

    Cho x-y=2. Tính giá trị biểu thức P = 2\left( {{x^3} - {y^3}} ight) - 3{\left( {x + y} ight)^2}.

    Hướng dẫn:

     Ta có:

    \begin{matrix} P = 2\left( {{x^3} - {y^3}} ight) - 3{\left( {x + y} ight)^2} \hfill \\ P = 2\left( {x - y} ight)\left( {{x^2} + xy + {y^2}} ight) - 3\left( {{x^2} + 2xy + {y^2}} ight) \hfill \\ P = 2\left( {x - y} ight)\left[ {{{\left( {x - y} ight)}^2} + 3xy} ight] - 3\left[ {{{\left( {x - y} ight)}^2} + 4xy} ight] \hfill \\ P = 2.2.\left( {{2^2} + 3xy} ight) - 3\left( {{2^2} + 4xy} ight) \hfill \\ P = 16 + 12xy - 12 - 12xy = 4 \hfill \\ \end{matrix}

  • Câu 5: Thông hiểu
    Tìm x

    Có bao nhiêu giá trị của x thỏa mãn x3 – 3x2 + 3 - x = 0

    Hướng dẫn:

     Ta có:

    \begin{matrix} {x^3}-3{x^2} + 3 - x = 0 \hfill \\ \Leftrightarrow {x^2}\left( {x - 3} ight) - \left( {x - 3} ight) = 0 \hfill \\ \Leftrightarrow \left( {{x^2} - 1} ight)\left( {x - 3} ight) = 0 \hfill \\ \Leftrightarrow \left( {x - 1} ight)\left( {x + 1} ight)\left( {x - 3} ight) = 0 \hfill \\ \Leftrightarrow \left[ \begin{gathered} x - 1 = 0 \hfill \\ x + 1 = 0 \hfill \\ x - 3 = 0 \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} x = 1 \hfill \\ x = - 1 \hfill \\ x = 3 \hfill \\ \end{gathered} ight. \hfill \\ \end{matrix}

    Vậy có 3 giá trị của x thỏa mãn.

  • Câu 6: Thông hiểu
    Tìm x biết

    Giá trị của x thỏa mãn 2x\left( {x + 3} ight) + 2\left( {x + 3} ight) = 0 là ?

    Hướng dẫn:

    Ta có:

    \begin{matrix} 2x\left( {x + 3} ight) + 2\left( {x + 3} ight) = 0 \hfill \\ \Rightarrow \left( {2x + 2} ight)\left( {x + 3} ight) = 0 \hfill \\ \Rightarrow 2\left( {x + 1} ight)\left( {x + 3} ight) = 0 \hfill \\ \Rightarrow \left[ \begin{gathered} x + 1 = 0 \hfill \\ x + 3 = 0 \hfill \\ \end{gathered} ight. \Rightarrow \left[ \begin{gathered} x = - 1 \hfill \\ x = - 3 \hfill \\ \end{gathered} ight. \hfill \\ \end{matrix}

    Vậy x = - 3 hoặc x = - 1.

  • Câu 7: Thông hiểu
    Xác định số giá trị x thỏa mãn điều kiện

    Có bao nhiêu giá trị của x thỏa mãn

    {\left( {x + 5} ight)^2} - 2\left( {x + 5} ight)\left( {x - 2} ight) + {\left( {x - 2} ight)^2} = 49

    Hướng dẫn:

    Ta có:

    \begin{matrix} {\left( {x + 5} ight)^2} - 2\left( {x + 5} ight)\left( {x - 2} ight) + {\left( {x - 2} ight)^2} = 49 \hfill \\ \Leftrightarrow {\left( {x + 5 - x + 2} ight)^2} = 49 \hfill \\ \Leftrightarrow {\left( 7 ight)^2} = 49 \hfill \\ \end{matrix}

    Luôn đúng với mọi giá trị x

  • Câu 8: Thông hiểu
    Thực hiện phép tính

    Kết quả của phép chia \left( {7{x^3} - 7x + 42} ight):\left( {{x^2} - 2x + 3} ight) là ?

    Hướng dẫn:

     Thực hiện phép chia như sau:

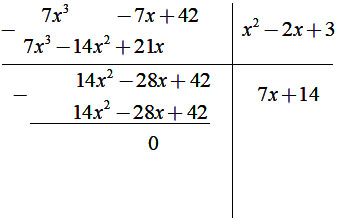
    Chia đa thức cho đa thức

  • Câu 9: Thông hiểu
    Xác định giá trị biểu thức

    Cho S = 1 + x + x2 + x3 + x4 + x5, chọn câu đúng

    Hướng dẫn:

     Ta có:

    \begin{matrix} xS = x + {x^2} + {x^3} + {x^4} + {x^5} + {x^6} \hfill \\ S = 1 + x + {x^2} + {x^3} + {x^4} + {x^5} \hfill \\ \Rightarrow xS - S = x + {x^2} + {x^3} + {x^4} + {x^5} + {x^6} \hfill \\ - \left( {1 + x + {x^2} + {x^3} + {x^4} + {x^5}} ight) \hfill \\ \Rightarrow xS - S = {x^6} - 1 \hfill \\ \end{matrix}

  • Câu 10: Vận dụng
    Tìm các hệ số a, b, c

    Xác định các hệ số a,b,c  biết \left( {{x^2} + cx + 2} ight)\left( {ax + b} ight) = {x^3} - {x^2} + 2;\forall x

    Hướng dẫn:

     Ta có:

    \begin{matrix} \left( {{x^2} + cx + 2} ight)\left( {ax + b} ight) = {x^3} - {x^2} + 2 \hfill \\ \Leftrightarrow a{x^3} + b{x^2} + ac{x^2} + bcx + 2ax + 2b = {x^3} - {x^2} + 2 \hfill \\ \Leftrightarrow a{x^3} + \left( {b + ac} ight){x^2} + \left( {bc + 2a} ight)x + 2b = {x^3} - {x^2} + 2 \hfill \\ \Leftrightarrow \left\{ \begin{gathered} a = 1 \hfill \\ b + ac = - 1 \hfill \\ bc + 2a = 0 \hfill \\ 2b = 2 \hfill \\ \end{gathered} ight.\hfill\\ \Rightarrow \left\{ \begin{gathered} a = 1 \hfill \\ b = 1 \hfill \\ c = - 2 \hfill \\ \end{gathered} ight. \hfill \\ \end{matrix}

  • Câu 11: Vận dụng
    Tìm giá trị của m

    Cho khai triển {\left( {x - 2y + m} ight)^4}. Tìm m để tổng các hệ số của khai triển bằng 0.

    Hướng dẫn:

    Tổng các hệ số của khai triển là giá trị của biểu thức tại x=y=1

    Vậy tổng các hệ số của khai triển là: {\left( {1 - 2.1 + m} ight)^4} = {\left( {m - 1} ight)^4}

    Để tổng các hệ số khai triển bằng 0 thì {\left( {m - 1} ight)^4} = 0 \Leftrightarrow m = 1

  • Câu 12: Thông hiểu
    Tính giá trị của biểu thức

    Tính giá trị của biểu thức x\left( {x - y} ight) + y\left( {x + y} ight) tại x=-6;y=8

    Hướng dẫn:

     Thu gọn biểu thức như sau:

    x\left( {x - y} ight) + y\left( {x + y} ight) = {x^2} + {y^2}

    Thay giá trị x; y đã cho vào biểu thức ta được

    {x^2} + {y^2} = {\left( { - 6} ight)^2} + {8^2} = 100

  • Câu 13: Nhận biết
    Thực hiện phép tính

    Tích của đơn thức x và đa thức (1 – x) là:

    Hướng dẫn:

    Thực hiện phép tính như sau:

    x\left( {1 - x} ight) = x.1 - x.x = x - {x^2}

  • Câu 14: Thông hiểu
    Phân tích đa thức thành nhân tử

    Phân tích đa thức {x^3}-6{x^2}y{\text{ }} + 12x{y^2}-8{y^3} thành nhân tử

    Hướng dẫn:

     Ta có:

    \begin{matrix} {x^3}-6{x^2}y{\text{ }} + 12x{y^2}-8{y^3} \hfill \\ = \left( {{x^3}-8{y^3}} ight)-\left( {6{x^2}y - 12x{y^2}} ight) \hfill \\ = \left( {x - 2y} ight)\left( {{x^2} + 2xy + 4{y^2}} ight)-6xy\left( {x - 2y} ight) \hfill \\ = \left( {x - 2y} ight)\left( {{x^2} + 2xy + 4{y^2}-6xy} ight) \hfill \\ = \left( {x - 2y} ight)\left( {{x^2} - 4xy + 4{y^2}} ight) \hfill \\ = \left( {x - 2y} ight){\left( {x - 2y} ight)^2} = {\left( {x - 2y} ight)^3} \hfill \\ \end{matrix}

  • Câu 15: Thông hiểu
    Thu gọn biểu thức

    Thực hiện phép tính \left( {5x - 1} ight)\left( {x + 3} ight) - \left( {x - 2} ight)\left( {5x - 4} ight) ta có kết quả là ?

    Hướng dẫn:

    Ta có:

    \begin{matrix} \left( {5x - 1} ight)\left( {x + 3} ight) - \left( {x - 2} ight)\left( {5x - 4} ight) \hfill \\ = 5{x^2} + 15x - x - 3 - 5{x^2} + 4x + 10x - 8 \hfill \\ = 28x - 11 \hfill \\ \end{matrix}

0/15
15 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (7%):
    2/3
  • Thông hiểu (67%):
    2/3
  • Vận dụng (27%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 65 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 8 CD

Đăng nhập