Cho tam giác ABC vuông tại A có ![]() . Khi đó độ dài cạnh
. Khi đó độ dài cạnh ![]() là:
là:
Hình vẽ minh họa
Ta có tam giác ABC vuông tại A nên
.
Cho tam giác ABC vuông tại A có ![]() . Khi đó độ dài cạnh
. Khi đó độ dài cạnh ![]() là:
là:
Hình vẽ minh họa
Ta có tam giác ABC vuông tại A nên
.
Quan sát hình vẽ:

Hệ thức nào sau đây sai?
Hệ thức sai là
Sửa lại:
Biết ![]() . Tính giá trị biểu thức
. Tính giá trị biểu thức ![]() ?
?
Ta có
Thay vào biểu thức C thu gọn ta được:
Cho tam giác ![]() vuông tại
vuông tại ![]() có
có ![]() và
và ![]() . Độ dài cạnh AC bằng:
. Độ dài cạnh AC bằng:
Ta có:
Một người dùng giác kế, đứng cách cái cây 10m rồi chỉnh thước ngắm cao bằng mắt để xác định góc “nâng” (góc tạo bởi tia sáng từ ngọn cây đến mắt tạo với phương ngang). Khi đó góc “nâng” đo được bằng ![]() . Tính chiều cao cái cây, biết rằng khoảng cách từ mặt đất đến mắt của người đo bằng
. Tính chiều cao cái cây, biết rằng khoảng cách từ mặt đất đến mắt của người đo bằng ![]() . (Kết quả làm tròn đến chữ số thập phân thứ nhất).
. (Kết quả làm tròn đến chữ số thập phân thứ nhất).
Hình vẽ minh họa
Giả sử BC là chiều cao của cây.
Áp dụng hệ thức lượng trong tam giác OAB vuông tại A ta có:
Chiều cao cây là:
Cho tam giác ![]() cân tại
cân tại ![]() có
có ![]() và góc ở đáy bằng
và góc ở đáy bằng ![]() . Độ dài cạnh đáy của tam giác cân bằng bao nhiêu? (Kết quả làm tròn đến chữ số thập phân thứ nhất).
. Độ dài cạnh đáy của tam giác cân bằng bao nhiêu? (Kết quả làm tròn đến chữ số thập phân thứ nhất).
Hình vẽ minh họa
Kẻ tại H, do tam giác ABC cân nên AH vừa là đường cao vừa là đường trung tuyến, phân giác
=> H là trung điểm của BC
Xét tam giác ABH vuông tại H ta có:
Một cầu trượt trong công viên có độ dốc ![]() và có độ cao là
và có độ cao là ![]() . Tính độ dài của cầu trượt. (Kết quả làm tròn đến chữ số thập phân thứ hai).
. Tính độ dài của cầu trượt. (Kết quả làm tròn đến chữ số thập phân thứ hai).
Hình vẽ minh họa
Độ dài cầu trượt là BC
Chiều cao của cầu trượt là AC = 2m
Độ dốc của cầu trượt là
Xét tam giác ABC vuông tại A ta có:
Vậy chiều dài cầu trượt là 3,77m.
Cho tam giác ![]() có diện tích
có diện tích ![]() . Điểm
. Điểm ![]() nằm giữa
nằm giữa ![]() sao cho
sao cho ![]() , điểm
, điểm ![]() nằm giữa
nằm giữa ![]() sao cho
sao cho ![]() . Hai điểm
. Hai điểm ![]() ở giữa
ở giữa ![]() sao cho
sao cho ![]() . Xác định diện tích tam giác
. Xác định diện tích tam giác ![]() ?
?
Hình vẽ minh họa
Ta có: (do chung đỉnh D và cạnh đáy cùng nằm trên BE)
(Do cùng đáy BE)
(Do chung đỉnh B và cạnh đáy nằm trên BC).
Vậy
Một cột đèn trên mặt đất dài ![]() . Các tia nắng mặt trời tạo với mặt đất một góc
. Các tia nắng mặt trời tạo với mặt đất một góc ![]() . Chiều cao của cột đèn gần nhất với giá trị nào sau đây?
. Chiều cao của cột đèn gần nhất với giá trị nào sau đây?
Hình vẽ minh họa
Ta có chiều cao cột đèn là AC
Chiều dài của bóng cột đèn là 8m
Tia nắng mặt trời tạo với mặt đất góc
Xét tam giác ABC vuông tại A ta có
Vậy chiều cao cột đèn khoảng 8m.
Cho hình vẽ:

Chọn hệ thức đúng?
Xét tam giác ADB vuông tại A ta có:
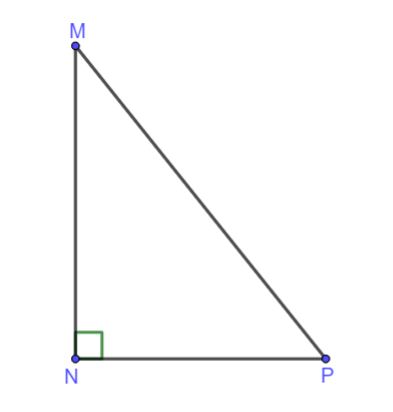
Cho tam giác MNP vuông tại N. Hệ thức nào sau đây là đúng?
Hình vẽ minh họa
Cho hình vẽ:

Tính giá trị ![]() ?
?
Áp dụng hệ thức lượng cho tam giác OAB vuông ta có:
Độ dài là:
Quan sát hình vẽ:

Hệ thức nào sau đây đúng?
Xét tam giác vuông tại A ta có:
Cho tứ giác ![]() có
có ![]() là giao điểm hai đường chéo. Biết
là giao điểm hai đường chéo. Biết ![]() . Tính diện tích tứ giác
. Tính diện tích tứ giác ![]() ?
?
Hình vẽ minh họa
Kẻ ta có:
Diện tích tứ giác là:
Tính chiều cao cột điện như hình vẽ:

Biết rằng ![]() . (Kết quả làm tròn đến hàng đơn vị).
. (Kết quả làm tròn đến hàng đơn vị).
Ta có:
Vậy chiều cao cột điện là 17m.
Một cột đèn cao ![]() có bóng in trên mặt đất dài
có bóng in trên mặt đất dài ![]() . Xác định góc tạo bởi tia sáng mặt trời tạo với mặt đất?
. Xác định góc tạo bởi tia sáng mặt trời tạo với mặt đất?
Hình vẽ minh họa
Xét tam giác ABC vuông tại B ta có:
Cho hình vẽ:

Tính độ lớn góc ![]() ? Kết quả làm tròn đến phút.
? Kết quả làm tròn đến phút.
Ta có:
Suy ra tam giác ABC vuông tại A (theo định lí Pythagore đảo)
Sắp xếp các tỉ số lượng giác sau theo thứ tự giảm dần: ![]() là:
là:
Ta có:
Mà
Vậy thứ tự cần sắp xếp là
Quan sát từ đỉnh một tòa nhà cao 70m người ta thấy một chiếc xe đỗ ở vị trí A (như hình vẽ minh họa):

Tính khoảng cách từ A đến B. (Kết quả làm tròn đến chữ số thập phân thứ nhất).
Ta có: (so le trong)
Do đó:
Một khúc sông rộng khoảng ![]() . Một chiếc thuyền muốn qua sông theo phương ngang nhưng bị dòng nước đẩy theo phương xiên nên phải đi khoảng 300m mới sang được vờ bên kia. Hỏi dòng nước đã đẩy thuyền lệch đi một khoảng bằng bao nhiêu độ?
. Một chiếc thuyền muốn qua sông theo phương ngang nhưng bị dòng nước đẩy theo phương xiên nên phải đi khoảng 300m mới sang được vờ bên kia. Hỏi dòng nước đã đẩy thuyền lệch đi một khoảng bằng bao nhiêu độ?
Hình vẽ minh họa
Ta có: Khúc sông AC dài 200m
Quãng đường thuyền di chuyển là BC = 300m
Góc lệch
Xét tam giác ABC vuông tại A ta có:
