Luyện tập Vị trí tương đối của đường thẳng và đường tròn KNTT

Nhận biết Thông hiểu Vận dụng Vận dụng cao

Bài kiểm tra này bao gồm 20 câu
Điểm số bài kiểm tra: 20 điểm
Xem lại kỹ lý thuyết trước khi làm bài
Chuẩn bị giấy và bút để nháp trước khi bắt đầu

Bắt đầu!!

00:00:00

Câu 1: Nhận biết
Xác định số điểm chung nhiều nhất
Đường thẳng và đường tròn có nhiều nhất bao nhiêu điểm chung?
- A.
  $1$
- B.
  $2$
- C.
  $3$
- D.
  $0$
Hướng dẫn:
Đường tròn và đường tròn có nhiều nhất hai điểm chung (trường hợp đường thẳng cắt đường tròn).
Câu 2: Nhận biết
Tính số đo góc AMB
Từ một điểm $M$ nằm ngoài đường tròn $(O)$ . Kẻ tiếp tuyến $MA;MB$ với đường tròn (với $A;B$ là các tiếp điểm. Nếu góc $\widehat{AOB} = 120^{0}$ thì góc $\widehat{AMB}$ có số đo bằng:
- A.
  $45^{0}$
- B.
  $75^{0}$
- C.
  $30^{0}$
- D.
  $60^{0}$
Hướng dẫn:
Xét tứ giác $OAMB$ có:

$\widehat{OAM} + \widehat{AMB} + \widehat{MBO} + \widehat{BOA} = 360^{0}$

$\Leftrightarrow 90^{0} + \widehat{AMB} + 90^{0} + 120^{0} = 360^{0}$

$\Leftrightarrow \widehat{AMB} = 60^{0}$
Câu 3: Vận dụng
Tìm quỹ tích điểm M
Cho đường tròn $(O;R)$ và một điểm $A$ chạy trên đường tròn đó. Kẻ đường thẳng $xy$ vuông góc với $OA$ . Trên $xy$ lấy điểm $M$ sao cho $AM = R\sqrt{3}$ . Điểm $M$ di động trên đường nào?
- A.
  Đường tròn tâm O bán kính $3R$
- B.
  Đường tròn tâm O bán kính $R$
- C.
  Đường tròn tâm O bán kính $4R$
- D.
  Đường tròn tâm O bán kính $2R$
Hướng dẫn:
Hình vẽ minh họa

Ta có: $OA\bot xy$

Xét tam giác OAM vuông tại A ta có:

$OM^{2} = OA^{2} + AM^{2} = 4R^{2}$

$\Rightarrow OM = 2R$

Suy ra khi A chạy trên đường tròn $(O;R)$ thì điểm M thuộc đường tròn tâm O bán kính 2R.
Câu 4: Thông hiểu
Xác định kết luận đúng
Cho tam giác $ABC$ có $AB = 3cm;AC = 4cm;BC = 5cm$ . Kết luận nào sau đây đúng?
- A.
  $AB$ là tiếp tuyến của đường tròn $(B;3cm)$
- B.
  $BC$ là tiếp tuyến của đường tròn $(C;3cm)$
- C.
  $BC$ là tiếp tuyến của đường tròn $(A;2,4cm)$
- D.
  $AB$ là tiếp tuyến của đường tròn $(A;4cm)$
Hướng dẫn:
Ta có:

$AB^{2} + AC^{2} = BC^{2}$ suy ra tam giác ABC vuông tại A

Kẻ đường cao AD ta chứng minh được $\Delta ADB\sim\Delta CAB(g - g)$

$\Rightarrow \frac{AD}{AC} = \frac{AB}{BC} \Rightarrow AD.BC = AB.AC$

$\Rightarrow AD.5 = 3.4 \Rightarrow AD = \frac{12}{5}$

Xét $(A;2,4cm)$ có $R = 2,4$

Vì $AD\bot BC$ tại D nên khoảng cách từ A đến BC là $d = AD = 2,4cm$

Vậy BC là tiếp tuyến của đường tròn $(A;2,4cm)$ .
Câu 5: Vận dụng
Tứ giác AMON là hình gì
Từ một điểm A ở bên ngoài đường tròn (O; R), vẽ hai tiếp tuyến AB, AC với (O). Đường thẳng vuông góc với OB tại O cắt tia AC tại N. Đường thẳng vuông góc với OC cắt tia AB tại M. Tứ giác AMON là hình gì?
- A.
  Hình bình hành
- B.
  Hình chữ nhật
- C.
  Hình thang
- D.
  Hình thoi
Hướng dẫn:
Hình vẽ minh họa
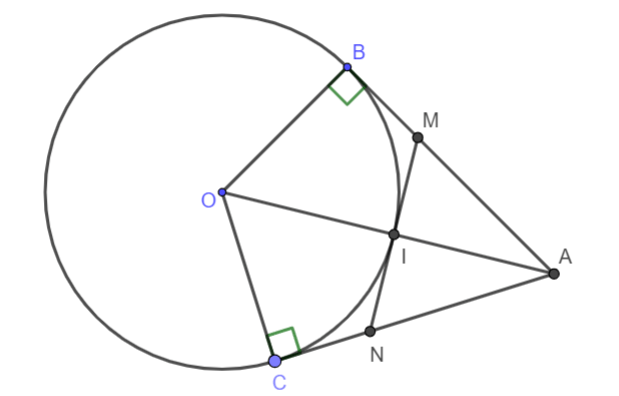
Xét tứ giác AMNO ta có:
Vì AM; ON cùng vuông góc với OB => AM // ON
Tương tự AN, OM cùng vuông góc với OC => AN // ON
=> AMON là hình bình hành
Xét hai tam giác vuông OBM và OCN ta có:
OB = OC = R
$\widehat {MOB} = \widehat {NOC}$ (cùng phụ với góc $\widehat {MON}$ )
=> $\Delta OBM = \Delta OCN \Rightarrow OM = ON$
=> Tứ giác AMON là hình thoi.
Câu 6: Nhận biết
Chọn khẳng định sai
Cho hai tiếp tuyến của đường tròn cắt nhau tại một điểm. Chọn khẳng định sai?
- A.
  Tai nối từ hai điểm đó là tia phân giác của góc tạo bởi hai bán kính.
- B.
  Tia nối từ điểm đó tới tâm là tia phân giác của góc tạo bởi hai bán kính.
- C.
  Khoảng cách từ điểm đó đến hai tiếp điểm là bằng nhau.
- D.
  Tia nối từ điểm đó tới tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
Hướng dẫn:
Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì:

Điểm đó cách đều hai tiếp điểm

Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.

Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm.

Vậy khẳng định sai là: “Tia nối từ điểm đó tới tâm là tia phân giác của góc tạo bởi hai bán kính.”
Câu 7: Thông hiểu
Xác định vị trí tương đối của đường tròn và trục tọa độ
Trên mặt phẳng tọa độ Oxy cho điểm A(5; 6). Xác định vị trí tương đối của đường tròn (A; 5) với các trục tọa độ?
- A.
  Đường tròn tiếp xúc trục Oy.
- B.
  Đường tròn tiếp xúc với trục Ox.
- C.
  Đường tròn không cắt trục Oy.
- D.
  Đường tròn không cắt trục Ox.
Hướng dẫn:
Ta có:
Khoảng cách từ A đến trục Ox bằng 6 > R.
Đường tròn (A; R) cắt trục Ox tại 2 điểm phân biệt .
Khoảng cách từ A đến trục Oy bằng 5 = R..
=> Đường tròn (A; R) tiếp xúc với trục Oy.
Câu 8: Vận dụng cao
Tìm điều kiện của a thỏa mãn yêu cầu
Cho đường tròn $(O;R)$ có dây $AB = R$ . Trên tia $AB$ lấy điểm $M$ sao cho $AM = a$ . Qua $M$ vẽ đường thẳng $xy$ vuông góc với $AB$ . Nếu đường thẳng $xy$ và đường tròn $(O;R)$ chỉ có một điểm chung thì điều kiện của $a$ là:
- A.
  $a \leq \frac{3R}{2}$
- B.
  $a \geq \frac{3R}{2}$
- C.
  $a \geq \frac{R}{2}$
- D.
  $a \leq \frac{R}{2}$
Hướng dẫn:
Hình vẽ minh họa

Gọi N là trung điểm của AB. Ta có:

$ON\bot AM$ và $MN = a - \frac{R}{2}$

Gọi H là chân đường vuông góc kẻ từ O xuống xy ta có:

$ON\bot xy$ suy ra ONMH là hình chữ nhật, do đó:

$d(O;xy) = OH = MN = a - \frac{R}{2}$

Đường thẳng xy và đường tròn $(O;R)$ có điểm chung khi và chỉ khi

$d(O;xy) \leq R \Leftrightarrow a - \frac{R}{2} \leq R$

$\Leftrightarrow a \leq \frac{3R}{2}$

Vậy đường thẳng xy và đường tròn $(O;R)$ chỉ có điểm chung khi $a \leq \frac{3R}{2}$ .
Câu 9: Nhận biết
Hoàn thành khẳng định
Cho đường tròn $(O;R)$ và đường thẳng $a$ . Gọi $d$ là khoảng cách từ $O$ đến đường thẳng $a$ . Nếu $d \leq R$ thì:
- A.
  Đường tròn $(O;R)$ và đường thẳng $a$ có một điểm chung.
- B.
  Đường tròn $(O;R)$ và đường thẳng $a$ có hai điểm chung.
- C.
  Đường tròn $(O;R)$ và đường thẳng $a$ có nhiều hơn một điểm chung.
- D.
  Đường tròn $(O;R)$ và đường thẳng $a$ có ít nhất một điểm chung.
Hướng dẫn:
Đường tròn $(O;R)$ và đường thẳng a có một điểm chung $\Rightarrow d = R$

Đường tròn $(O;R)$ và đường thẳng $a$ có hai điểm chung $\Rightarrow d < R$

Đường tròn $(O;R)$ và đường thẳng $a$ không có điểm chung $\Rightarrow d > R$

=> Đường tròn $(O;R)$ và đường thẳng $a$ có ít nhất một điểm chung $\Rightarrow d \leq R$
Câu 10: Nhận biết
Tính số đo góc AMC
Cho đường tròn $(O;R)$ . Từ điểm $M$ nằm ngoài đường tròn kẻ các tiếp tuyến $MA;MB$ (với $A;B$ là các tiếp điểm). Xác định số đo góc $\widehat{AMC}$ biết rằng $\widehat{MAC} = 70^{0}$ ?
- A.
  $50^{0}$
- B.
  $70^{0}$
- C.
  $40^{0}$
- D.
  $60^{0}$
Hướng dẫn:
Hình vẽ minh họa

Theo tính chất tiếp tuyến ta có: MA = MB

Suy ra tam giác MAB cân tại M

$\Rightarrow \widehat{AMC} = 180^{0} - 2.\widehat{MAC} = 40^{0}$ .
Câu 11: Vận dụng
Tìm diện tích lớn nhất của ABCD
Cho nửa đường tròn tâm $O$ , đường kính $AB = 10cm$ . Điểm $M$ thuộc nửa đường tròn. Qua $M$ kẻ tiếp tuyến $xy$ với nửa đường tròn. Gọi $D;C$ lần lượt là hình chiếu của $A;B$ trên $xy$ . Diện tích lớn nhất của tứ giác $ABCD$ là:
- A.
  $45cm^{2}$
- B.
  $50cm^{2}$
- C.
  $60cm^{2}$
- D.
  $65cm^{2}$
Hướng dẫn:
Hình vẽ minh họa

Tứ giác ABCD là hình thang vuông, MO là đường trung bình của hình thang.

$\Rightarrow S_{ABCD} = \frac{CD.(AC + BD)}{2} = CD.OM$

$\leq AB.OM = 2R^{2} = 50cm^{2}$

Suy ra diện tích ABCD đạt giá trị lớn nhất là $50cm^{2}$ khi $CD//AB$ .
Câu 12: Thông hiểu
Tính độ dài AT
Cho đoạn thẳng $AC$ , $B \in AC$ sao cho $BC = 3BA$ . Gọi $AT$ là một tiếp tuyến của đường tròn đường kính $BC$ với $T$ là tiếp điểm. Biết $BC = 6cm$ . Độ dài đoạn thẳng $AT$ là:
- A.
  $8cm$
- B.
  $9cm$
- C.
  $4cm$
- D.
  $6cm$
Hướng dẫn:
Hình vẽ minh họa

Ta có: $BC = 6cm$ suy ra $R = 3cm; AB = 2cm$

Suy ra $AO = AB + BO = 2 + 3 = 5cm$

Áp dụng định lý Pythagore cho tam giác ATO vuông tại T (AT là tiếp tuyến của (O))) ta có:

$AT = \sqrt{AO^{2} - OT^{2}} = \sqrt{5^{2} - 3^{2}} = 4(cm)$
Câu 13: Thông hiểu
Tính diện tích tam giác OBC
Cho điểm $O$ cách đường thẳng $a$ là $6cm$ . Vẽ đường tròn $(O;10)$ . Gọi giao điểm của đường thẳng và đường tròn lần lượt là $B;C$ . Tính diện tích tam giác $OBC$ ?
- A.
  $36cm^{2}$
- B.
  $31cm^{2}$
- C.
  $48cm^{2}$
- D.
  $40cm^{2}$
Hướng dẫn:
Hình vẽ minh họa

Gọi H là chân đường vuông góc kẻ từ O xuống a

Suy ra $OH = 6cm$ và H là trung điểm của BC

Do đó $BH = \sqrt{OB^{2} - OH^{2}} = \sqrt{10^{2} - 6^{2}} = 8$

$\Rightarrow AC = 16cm$

Suy ra diện tích tam giác $OBC$ là:

$S_{OBC} = \frac{1}{2}OH.BC = \frac{1}{2}.6.16 = 48\left( cm^{2} ight)$
Câu 14: Nhận biết
Tìm điều kiện của OH
Cho đường thẳng $a$ và đường tròn $(O;6cm)$ . Gọi $OH$ là khoảng cách từ $O$ đến $a$ . Điều kiện để đường thẳng $a$ và $(O;6cm)$ có ít nhất một điểm chung là:
- A.
  $OH = 6cm$
- B.
  $OH < 6cm$
- C.
  $OH \leq 6cm$
- D.
  $OH \geq 6cm$
Hướng dẫn:
Ta có: $(O;6cm) \Rightarrow R = 6cm$

Đường thẳng a cắt $(O;6cm)$ $\Leftrightarrow d < R \Leftrightarrow OH < R$

Đường thẳng a tiếp xúc với $(O;6cm)$ $\Leftrightarrow d = R \Leftrightarrow OH = R$

Khi đó điều kiện để đường thẳng a và $(O;6cm)$ có ít nhất một điểm chung là: $OH \leq 6cm$
Câu 15: Thông hiểu
Tính số đo góc BAC
Cho đường tròn $(O;6cm)$ . Từ điểm $A$ cách tâm $O$ một khoảng bằng $12cm$ , kẻ các tiếp tuyến $AB;AC$ (với $B;C$ là các tiếp điểm). Xác định số đo góc $\widehat{BAC}$ ?
- A.
  $75^{0}$
- B.
  $30^{0}$
- C.
  $45^{0}$
- D.
  $60^{0}$
Hướng dẫn:
Hình vẽ minh họa

Xét tam giác OAB vuông tại B có:

$\sin\widehat{OAB} = \frac{OB}{OA} = \frac{6}{12} = \frac{1}{2}$

$\Rightarrow \widehat{BAO} = 30^{0} \Rightarrow \widehat{BAC} = 2\widehat{BAO} = 60^{0}$
Câu 16: Nhận biết
Chọn đáp án đúng
Cho đường thẳng $a$ và đường tròn $(O;5cm)$ . Biết khoảng cách từ $O$ đến đường thẳng $a$ là $2,5cm$ . Khi đó:
- A.
  Đường thẳng $a$ tiếp xúc với đường tròn $(O;5cm)$ .
- B.
  Đường thẳng $a$ và đường tròn $(O;5cm)$ không có điểm chung.
- C.
  Đường thẳng $a$ và đường tròn $(O;5cm)$ không giao nhau.
- D.
  Đường thẳng $a$ và đường tròn $(O;5cm)$ cắt nhau.
Hướng dẫn:
Vì khoảng cách từ tâm O của đường tròn $(O;5cm)$ đến đường thẳng a là 2,5cm

$\Rightarrow d = 2,5cm < R = 5cm$

Suy ra đường thẳng a và đường tròn $(O;5cm)$ cắt nhau.
Câu 17: Thông hiểu
Chọn phát biểu đúng
Cho tam giác ABC cân tại đỉnh A, nội tiếp đường tròn (O). Phát biểu nào sau đây là đúng?
- A.
  Tiếp tuyến tại A của đường tròn (O) là đường thẳng qua A và vuông góc với AC.
- B.
  Tiếp tuyến tại A với đường tròn (O) là đường thẳng qua A và vuông góc với AB.
- C.
  Tiếp tuyến tại A với đường tròn (O) là đường thẳng qua A và song song với BC.
- D.
  Tiếp tuyến tại A với đường tròn (O) là đường thẳng qua A và vuông góc với BC.
Hướng dẫn:
Vì tam giác ABC cân tại A => Tâm đường tròn ngoại tiếp nằm trên đường cao của tam giác đi qua A hay OA vuông góc với BC mà tiếp tuyến của (O) tại A thì cũng phải vuông góc với OA( tính chất tiếp tuyến của đường tròn).
=> Tiếp tuyến tại A của đường tròn sẽ song song với BC.
Câu 18: Thông hiểu
Tính số đo góc ABO
Cho đường tròn $(O)$ , hai tiếp tuyến của đường tròn tại $A;B$ cắt nhau tại $M$ . Biết $\widehat{AMB} = 50^{0}$ . Tính số đo góc $\widehat{ABO}$ ?
- A.
  $50^{0}$
- B.
  $25^{0}$
- C.
  $90^{0}$
- D.
  $130^{0}$
Hướng dẫn:
Xét tứ giác AMBO có:

$\widehat{AOB} = 360^{0} - 2.90^{0} - 50^{0} = 130^{0}$

Tam giác OAB cân tại O có $\widehat{AOB} = 130^{0}$ nên

$\widehat{ABO} = \frac{180^{0} -130^{0}}{2} = 25^{0}$
Câu 19: Thông hiểu
Tìm độ dài đoạn AD
Cho đường tròn $(O;2cm)$ . Một đường thẳng đi qua điểm $A$ nằm bên ngoài đường tròn và cắt đường tròn tại $B;C$ sao cho $AB = BC$ . Kẻ đường kính $CD$ . Tính độ dài đoạn thẳng $AD$ ?
- A.
  $6cm$
- B.
  $4cm$
- C.
  $8cm$
- D.
  $10cm$
Hướng dẫn:
Hình vẽ minh họa

Trong tam giác ACD có:

O là trung điểm của CD; B là trung điểm của AC

Nên OB là đường trung bình tam giác $ACD$

Do đó $OB = \frac{1}{2}AD \Rightarrow AD = 2.2 = 4cm$
Câu 20: Thông hiểu
Tìm độ dài cạnh EF
Cho đường tròn $(O;15cm)$ và dây $AB = 24cm$ . Một tiếp tuyến song song với $AB$ cắt các tia $OA;OB$ theo thứ tự $E$ và $F$ . Tính độ dài $EF$ ?
- A.
  $20cm$
- B.
  $42cm$
- C.
  $48cm$
- D.
  $40cm$
Hướng dẫn:
Hình vẽ minh họa

Gọi G là tiếp tuyến của EF với (O), H là trung điểm của AB. Khi đó ta có:

$OH = \sqrt{R^{2} - \left( \frac{AB}{2} ight)^{2}} = \sqrt{15^{2} - 12^{2}} = 9(cm)$

Vì $AB//EF$ nên $\frac{AB}{EF} = \frac{OH}{OG}$

$\Rightarrow EF = \frac{AB.OG}{OH} = \frac{24.15}{9} = 40(cm)$