Luyện tập Cung và dây của một đường tròn Kết nối tri thức

Vì đường tròn có bán kính 15cm nên đường kính có độ dài là 30cm. Đáy lớn nhất trong đường tròn là đường kính.

Vì tam giác OAB cân tại O nên

Suy ra số đo cung nhỏ là

Vì tam giác OCD cân tại O nên

Suy ra số đo cung nhỏ AB là

Xét tam giác ABC cân tại A ta có:

Xét tam giác OIB có

Suy ra tam giác OIB cân tại O

Xét tam giác OKC có

Suy ra tam giác OKC cân tại O

Do tam giác OAC vuông tại A nên

Mà là góc ở tâm chắn cung AB nên

Trong các dây của một đường tròn, đường kính là dây có độ dài lớn nhất.

“Nếu E là một điểm nằm trên cung AB thì ” là khẳng định đúng.

Hình vẽ minh họa

Xét tam giác OIM vuông tại I ta có:

Tam giác MON cân tại O có OI vừa là đường cao vừa là đường phân giác nên

Suy ra số đo cung nhỏ MN là .

Vì thì dây AB là đường kính, còn thì dây AB không là đường kính.

Vậy đáp án chính xác là .

Ta có:

Nên số đo cung AB nhỏ là .

12 số trên mặt đồng hồ chia thành 12 cung với đơn vị bằng nhau.

Số đo trên mỗi cũng đơn vị là

Vào lúc 20 giờ, kim dài chỉ vào số 12 và kim phút chỉ vào số 8 nên góc ở tâm tạo bởi chúng chắn 4 cung đơn vị.

Vậy góc ở tâm lúc đó là

Hình vẽ minh họa

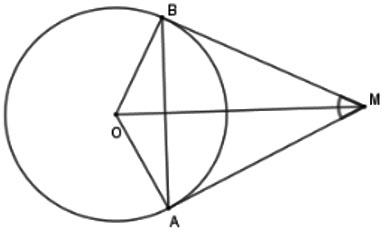
Xét tứ giác OAMB ta có:

=> Số đo cung nhỏ AB là ; Số đo cung lớn AB là .

Khi hai mút của cung trùng nhau ta có “cung không” với số đo .

Tam giác ABC là tam giác đều có tất cả các góc bằng 600⁰ nên chia đường tròn thành ba cung bằng nhau.

Suy ra số đo mỗi cung là .

Suy ra số đo cung BC lớn là:

Một giờ đồng hồ, kim phút quay tương ứng với 60 hút. Phải quay nhanh thêm 25 phút nên góc quay là .

Hình vẽ minh họa

Do tam giác ACE đều nên

Do tứ giác nội tiếp nên

Tương tự ta cũng có

Góc có đỉnh trùng với tâm của đường tròn gọi là góc ở tâm.

Số đo của cung lớn bằng hiệu giữa và số đo cung nhỏ (có chung hai mút với cung lớn).

Xét đường tròn (O) ta có:

(vì BC là đường kính)

Suy ra số đo cung nhỏ BD là:

Số đo cung nhỏ AD là:

Số đo cung nhỏ AC là

nhỏ = nhỏ + nhỏ =

nhỏ = nhỏ + nhỏ =

Suy ra hai cung nhỏ cần tìm có mối quan hệ là .

Vậy đáp án chính xác nhất là:

Hình vẽ minh họa

Ta có:

Xét đường tròn có tại nên là trung điểm của

Xét tam giác vuông tại H có:

Mà tam giác OCD cân tại O có OH là đường cao nên OH cũng là đường phân giác

Do đó số đo cung nhỏ CD là , số đo cung lớn CD là .