Lớp 9 Toán 9 - Kết nối tri thức

Luyện tập Vị trí tương đối của hai đường tròn Kết nối tri thức

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Nhận biết
    Tính diện tích hình vành khăn

    Cho hai đường tròn (O;8cm) và (O;5cm). Diện tích hình vành khăn bằng bao nhiêu? (Kết quả làm tròn đến chữ số thập phân thứ nhất).

    Hướng dẫn:

    Hình vẽ minh họa

    Diện tích hình vành khăn là:

    S_{vk} = \pi R^{2} - \pi R'^{2} = \pi\left( 8^{2} - 5^{2} ight) = 3,14.39 = 122,5cm^{2}

    Vậy diện tích cần tìm là 122,5cm^{2}

  • Câu 2: Thông hiểu
    Xác định vị trí tương đối của hai đường tròn

    Cho hình vuông ABCD cạnh bằng 2cm. Gọi I;J lần lượt là trung điểm của AC;CD. Vị trí tương đối của đường tròn (A;AI) và (C;CJ) là:

    Hướng dẫn:

    Áp dụng định lí Pythagore cho \Delta ABC vuông tại A có:

    BC^{2} = AB^{2} + AC^{2} \Rightarrow AC = 2\sqrt{2}(cm)

    \Rightarrow \left\{ \begin{matrix}AI = \dfrac{AC}{2} = \sqrt{2}(cm) \\CJ = \dfrac{CD}{2} = 1(cm) \\\end{matrix} ight.

    Ta có: AI + CJ < AC\left( 1 + \sqrt{2} < 2\sqrt{2} ight)

    Suy ra hai đường tròn ở vị trí ngoài nhau.

  • Câu 3: Thông hiểu
    Chọn khẳng định sai

    Cho nửa đường tròn (O), đường kính AB. Vẽ nửa đường tròn tâm O’ đường kính AO (cùng phía với nửa đường tròn (O)). Một cát tuyến bất kì qua A cắt (O’); (O) lần lượt tại C, D. Chọn khẳng định sai:

    Hướng dẫn:

    Hình vẽ minh họa

    Chọn khẳng định sai

    Xét nửa đường tròn (O’) có AO là đường kính và C ∈ (O’) nên

    ⇒ AD ⊥ CO

    Xét đường tròn (O) có OA = OD

    => ∆OAD cân tại O có OC là đường cao nên OC cũng là đường trung tuyến hay C là trung điểm của AD.

    Xét tam giác AOD có O’C là đường trung bình => O’C // OD

    Kẻ các tiếp tuyến Cx; Dy với các nửa đường tròn ta có:

    Cx ⊥ O’C; Dy ⊥ OD  mà O’C // OD

    => Cx //Dy

    => Phương án sai "Các tiếp tuyến tại C và D của các nửa đường tròn cắt nhau".

  • Câu 4: Nhận biết
    Điều kiện để hai đường tròn tiếp xúc trong

    Gọi d là khoảng cách 2 tâm của  và  với 0 < r < R. Để (O) và (O') tiếp xúc trong thì:

    Hướng dẫn:

    Để (O) và (O') tiếp xúc trong thì d = R - r

  • Câu 5: Thông hiểu
    Tính diện tích tam giác BCD

    Cho đường tròn (O;R) đường kính AB. M là một điểm nằm giữa A và B. Qua M vẽ dây CD vuông góc với AB. Biết AM = 4, R = 6,5. Giá trị diện tích tam giác BCD là bao nhiêu?

    Hướng dẫn:

    Hình vẽ minh họa:

    Tính diện tích tam giác BCD

    Ta có:

    \begin{matrix} OM = R - AM \hfill \\ \Rightarrow OM = 6,5 - 4 = 2,5 \hfill \\ \Rightarrow CM = \sqrt {{R^2} - O{M^2}} = 6 \hfill \\ \Rightarrow CD = 12 \hfill \\ \Rightarrow BM = BO + OM = R + OM = 6,5 + 2,5 = 9 \hfill \\ \Rightarrow S = \dfrac{1}{2}BM.CD = \dfrac{1}{2}.9.12 = 54 \hfill \\ \end{matrix}

  • Câu 6: Vận dụng
    Chọn câu đúng nhất

    Cho các đường tròn (A; 10cm), (B; 15cm), (C; 15cm) tiếp xúc ngoài với nhau đôi một. Hai đường tròn (B) và (C) tiếp xúc với nhau tại A’. Đường tròn (A) tiếp xúc với đường tròn (B) và (C) lần lượt tại C’ và B’. Chọn câu đúng nhất.

    Hướng dẫn:

    Hình vẽ minh họa

    Chọn câu đúng nhất

    Theo tính chất đoạn nối tâm của hai đường tròn tiếp xúc ngoài ta có:

    AB = BC’ + C’A = 25cm

    AC = AB’ + B’C = 25cm

    BC = BA’ + A’C = 30cm và A’ là trung điểm của BC (vì A’B = A’C = 15cm)

    ABC cân tại A có AA’ là đường trung tuyến nên cũng là đường cao

    ⇒ AA’ ⊥ BC

    => AA’ là tiếp tuyến chung của hai đường tròn (B) và (C)

    Xét tam giác AA’C vuông tại A’ có:

    A’A^2 = AC^2 – A’C^2 = 25^2 – 15^2 = 400

    ⇒ A’A = 20cm

  • Câu 7: Thông hiểu
    Tính độ dài BC

    Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, B∈(O) và C∈(O’). Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC tại I. Tính độ dài BC biết OA = 9cm, O’A = 4cm.

    Hướng dẫn:

    Hình vẽ minh họa

    Tính độ dài BC

    Ta có IO là tia phân giác của \widehat {BIA}

    IO′ là tia phân giác của \widehat {CIA}

    Mà \widehat {BIA} + \widehat {CIA} = {180^0} \Rightarrow \widehat {OIO'} = {90^0}

    Tam giác OIO′ vuông tại I có IA là đường cao

    => IA^2=AO.AO′=9.4=36

    ⇒IA=6cm

    ⇒IA=IB=IC=6cm (tính chất hai tiếp tuyến cắt nhau)

    Vậy BC=2IA=2.6=12(cm)

  • Câu 8: Nhận biết
    Chọn đáp án đúng

    Hai đường tròn có hai tiếp tuyến chung trong thì vị trí tương đối của chúng là:

    Hướng dẫn:

    Hai đường tròn có hai tiếp tuyến chung trong thì vị trí tương đối của chúng là ngoài nhau.

  • Câu 9: Nhận biết
    Xác định độ dài OO'

    Hai đường tròn (O;2cm) và (O';5cm) tiếp xúc ngoài nên độ dài đoạn OO' bằng:

    Hướng dẫn:

    Vì hai đường tròn tiếp xúc ngoài nên OO' = R + R' = 2 + 5 = 7(cm)

  • Câu 10: Thông hiểu
    Tính độ dài OO'

    Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Biết OA = 6cm;AO' = 5cm;AB = 8cm (như hình vẽ)

    Tính độ dài OO'?

    Hướng dẫn:

    Vì OO’ là đường trung trực của AB nên IA = IB = \frac{8}{2} = 4(cm)

    Áp dụng định lí Pythagore cho tam giác vuông ta có:

    OI = \sqrt{OA^{2} - IA^{2}} = \sqrt{6^{2} - 4^{2}} = 2\sqrt{5}(cm)

    O'I = \sqrt{O'A^{2} - IA^{2}} = \sqrt{5^{2} - 4^{2}} = 3(cm)

    \Rightarrow OO' = OI + O'I = 2\sqrt{5} + 3(cm)

  • Câu 11: Nhận biết
    Tìm khẳng định sai

    Trong các câu sau, câu nào sai?

    Hướng dẫn:

    Nếu hai đường tròn (O;R) và (O';R') không giao nhau thì OO' > R + R'.

  • Câu 12: Thông hiểu
    Tìm vị trí tương đối của hai đường tròn

    Cho hình vuông ABCD có I;J lần lượt là trung điểm của AD;BC. Vị trí tương đối của hai đường tròn (I;IA) và (J;JB) là:

    Hướng dẫn:

    Hình vẽ minh họa

    Vì I; J lần lượt là trung điểm của AD và BC nên \left\{ \begin{matrix}IA = \dfrac{1}{2}.AD \\JB = \dfrac{1}{2}BC \\\end{matrix} ight.

    Hay \left\{ \begin{matrix}IA = \dfrac{1}{2}.AB \\JB = \dfrac{1}{2}AB \\\end{matrix} ight. (vì ABCD là hình vuông)

    Suy ra IA + JB = AB

    Mặt khác IJ = AB \Rightarrow IA + JB = IJ

    Vậy hai đường tròn (I;IA) và (J;JB) là tiếp xúc ngoài với nhau.

  • Câu 13: Vận dụng cao
    Tính tỉ số diện tích của hai hình quạt tròn

    Cho hai đường tròn (O;6cm) và (O';2cm) tiếp xúc ngoài tại A; BC là tiếp tuyến chung ngoài, B \in (O);C \in (O'). Tính tỉ số diện tích của hai hình quạt tròn AO'C và AOB?

    Hướng dẫn:

    Hình vẽ minh họa

    Ta có:

    BC\bot OB;BC\bot O'C (tiếp tuyến vuông góc với bán kính đi qua tiếp điểm)

    Suy ra \left\{ \begin{matrix} \widehat{C} = \widehat{B} = 90^{0} \\ OB//OC \\ \end{matrix} ight.

    Kẻ CD//OO';(D \in OB)

    Tứ giác ODCO' là hình bình hành

    \Rightarrow \left\{ \begin{matrix} CD = OO' = R + R' = 8cm \\ BD = OB - OD = 4cm \\ \end{matrix} ight.

    Tam giác BDC vuông tại B có CD = 2BD nên bằng nửa tam giác đều cạnh CD.

    \Rightarrow \widehat{BDC} = 60^{0} \Rightarrow \widehat{AOB} = \widehat{BDC} = 60^{0} (hai góc đồng vị)

    Ta có: \widehat{AOB} + \widehat{AO'C} = 180^{0} (hai góc trong cùng phía)

    \Rightarrow \widehat{AO'C} = 180^{0} - \widehat{AOB} = 180^{0} - 60^{0} = 120^{0}

    Khi đó tỉ số diện tích hai tam giác cần tìm là:

    \dfrac{S_{hqAO'C}}{S_{hqAOB}} =\dfrac{\dfrac{\pi.2^{2}.120}{360}}{\dfrac{\pi.6^{2}.60}{360}} =\dfrac{2}{9}

  • Câu 14: Nhận biết
    Chọn kết luận đúng

    Cho hai đường tròn (O;R) và (I;r) với R > r tiếp xúc ngoài, khi đó ta có:

    Hướng dẫn:

    Vì hai đường tròn (O;R) và (I;r) với R > r tiếp xúc ngoài nên OI = R + r.

  • Câu 15: Thông hiểu
    Tam giác ABC là hình gì

    Cho hai đường tròn (O_1) và (O_2) tiếp xúc ngoài tại A và một đường thẳng d tiếp xúc với (O_1); (O_2) lần lượt tại B, C. Tam giác ABC là:

    Hướng dẫn:

    Hình vẽ minh họa

    Tam giác ABC là hình gì

    Xét (O_1) có O_1B=O_1A

    => Tam giác O_1AB cân tại O_1

    => \widehat {{O_1}BA} = \widehat {{O_1}AB}

    Xét (O_2) có O_1C=O_1A

    => Tam giác O_2CA cân tại O_2

    => \widehat {{O_2}CA} = \widehat {{O_2}AC}

    Mà \widehat {{O_1}} + \widehat {{O_2}} = {360^0} - \left( {\widehat C + \widehat B} ight) = {180^0}

    \begin{matrix} \Leftrightarrow {180^0} - \left( {\widehat {{O_1}BA} + \widehat {{O_1}AB}} ight) + {180^0} \hfill \\ - \left( {\widehat {{O_2}CA} + \widehat {{O_2}AC}} ight) = {180^0} \hfill \\ \Leftrightarrow \widehat {{O_1}BA} + \widehat {{O_2}AC} = {90^0} \hfill \\ \Leftrightarrow \widehat {BAC} = {90^0} \hfill \\ \end{matrix}

    => Tam giác ABC vuông tại A.

  • Câu 16: Thông hiểu
    Tính độ dài cạnh AD

    Quan sát hình vẽ sau và xác định độ dài cạnh AD.

    Hướng dẫn:

    Xét tam giác OAG và tam giác O’AD ta có:

    \widehat{OAG} = \widehat{O'AD} (đối đỉnh)

    Mà \widehat{OAG} = \widehat{OGA} (tam giác OGA cân tại O) và \widehat{O'DA} = \widehat{O'AD} (tam giác O’DA cân tại O’)

    \Rightarrow \widehat{OGA} = \widehat{O'DA}

    Suy ra \Delta OAG\sim\Delta O'AD(g - g)

    \Rightarrow \frac{OA}{O'A} = \frac{AG}{AD} \Leftrightarrow \frac{4,5}{2} = \frac{7,5}{AD} \Rightarrow AD = \frac{10}{3}

  • Câu 17: Vận dụng
    Tính số đo các góc

    Cho hai đường tròn (O;6cm) và (O';2cm) tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài, \left( B \in (O),C \in (O') ight). Tính số đo các góc \widehat{AOB},\widehat{AO'C}.

    Hướng dẫn:

    Hình vẽ minh họa

    Ta có: \widehat{AOB} =45^{0},\widehat{AO'C} = 135^{0}(tiếp tuyến vuông góc với bán kính đi qua tiếp điểm).

    \Rightarrow \left\{ \begin{matrix}\widehat{B} = \widehat{C} = 90^{0} \\OB//O'C \\\end{matrix} ight.

    Vẽ CD//OO',(D \in OB)

    Tứ giác ODCO' là hình bình hành

    \Rightarrow \left\{ \begin{matrix}CD = OO' = R + R' = 8(cm) \\BD = OB - OD = 4(cm) \\\end{matrix} ight.

    Tam giác BCD vuông tại B có CD = 2BD nên bằng nửa tam giác đều cạnh CD.

    \Rightarrow \widehat{BDC} = 60^{0}\Rightarrow \widehat{AOB} = \widehat{BDC} = 60^{0}(hai góc đồng vị)

    Ta có:

    \widehat{AOB} + \widehat{AO'C} =180^{0} (hai góc trong cùng phía)

    \Rightarrow \widehat {AO'C} = {180^0} - \widehat {AOB} = {180^0} - {60^0} = {120^0}

    Vậy \widehat{AOB} =60^{0};\widehat{AO'C} = 120^{0}

  • Câu 18: Nhận biết
    Chọn đáp án đúng

    Hai đường tròn chỉ có một điểm chung được gọi là hai đường tròn:

    Hướng dẫn:

    Hai đường tròn chỉ có một điểm chung được gọi là hai đường tròn tiếp xúc nhau.

  • Câu 19: Thông hiểu
    Tứ giác MNPQ là hình gì

    Cho hai đường tròn (O); (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN với M ∈ (O); N ∈ (O’). Gọi P là điểm đối xứng với M qua OO’; Q là điểm đối xứng với N qua OO’. Khi đó, tứ giác MNQP là hình gì?

    Hướng dẫn:

     Hình vẽ minh họa

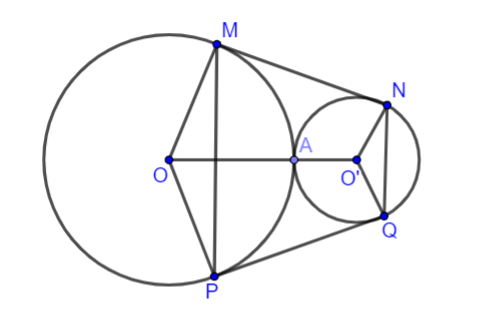
    Tứ giác MNPQ là hình gì

    Vì P là điểm đối xứng với M qua OO’

    Q là điểm đối xứng với N qua OO’ nên MN = PQ

    P ∈ (O); Q ∈ (O’) và MP ⊥ OO’; NQ ⊥ OO’ ⇒ MP // NQ mà MN = PQ

    => MNPQ là hình thang cân.

  • Câu 20: Thông hiểu
    Tính diện tích hình giới hạn bởi hai cung

    Cho hai đường tròn (O;8cm) và (O;5cm). Hai bán kính OM;ON của đường tròn lớn cắt đường tròn nhỏ tại E;F. Biết rằng \widehat{MON} = 100^{0}. Tính diện tích hình giới hạn bởi hai cung nhỏ MN và EF? (Kết quả làm tròn đến chữ số thập phân thứ nhất).

    Hướng dẫn:

    Hình vẽ minh họa

    Diện tích hình giới hạn bởi hai cung nhỏ MN và EF là:

    S = S_{hqMON} - S_{hqEOF}

    = \frac{\pi.8^{2}.100}{360} - \frac{\pi.5^{2}.100}{360}

    = 55,82 - 21,81 = 34,01

    Vậy diện tích cần tìm là 34,01cm^{2}

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (35%):
    2/3
  • Thông hiểu (50%):
    2/3
  • Vận dụng (10%):
    2/3
  • Vận dụng cao (5%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 3 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 9 KNTT

Đăng nhập