Cho tam giác ABC có góc A bằng ![]() ,
, ![]() m. Tính độ dài đường phân giác AD?
m. Tính độ dài đường phân giác AD?
Hình vẽ minh họa:
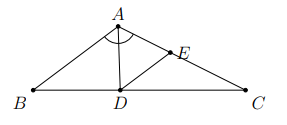
Kẻ
Chứng minh được tam giác đều.
Đặt . Ta có:
Vậy
Cho tam giác ABC có góc A bằng ![]() ,
, ![]() m. Tính độ dài đường phân giác AD?
m. Tính độ dài đường phân giác AD?
Hình vẽ minh họa:

Kẻ
Chứng minh được tam giác đều.
Đặt . Ta có:
Vậy
Cho tam giác ACE có ![]() . Lấy điểm B trên cạnh AC sao cho
. Lấy điểm B trên cạnh AC sao cho ![]() . Lấy điểm D trên cạnh AE sao cho
. Lấy điểm D trên cạnh AE sao cho ![]() . Chọn khẳng định đúng.
. Chọn khẳng định đúng.
Xét tam giác có:
Khi đó theo định lí Thalès ta có:
Cho tam giác ![]() vuông tại
vuông tại ![]() . Lấy điểm
. Lấy điểm ![]() thuộc
thuộc ![]() ,
, ![]() thuộc
thuộc ![]() sao cho
sao cho ![]() ,
, ![]() . Khi đó độ dài cạnh
. Khi đó độ dài cạnh ![]() là:
là:
Hình vẽ minh họa
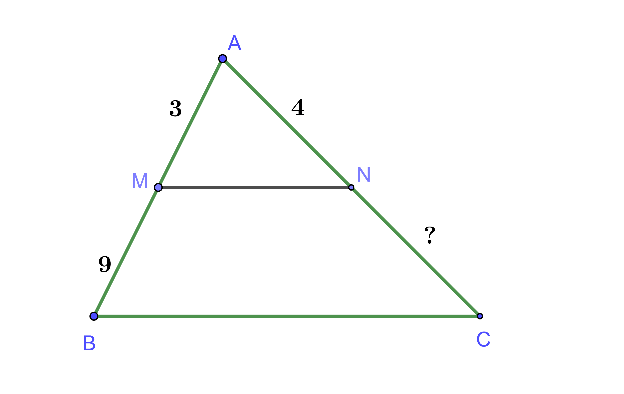
Vì nên theo hệ quả của định lí Talet ta có:
Tìm x trong hình vẽ sau:

Ta có:
Cho tam giác ![]() có
có ![]() . Lấy điểm
. Lấy điểm ![]() trên cạnh
trên cạnh ![]() sao cho
sao cho ![]() . Lấy điểm
. Lấy điểm ![]() trên cạnh
trên cạnh ![]() sao
sao ![]() . Giả sử
. Giả sử ![]() . Khi đó:
. Khi đó:
Độ dài cạnh ![]() là 2
là 2
Độ dài cạnh ![]() là 4
là 4
Cho tam giác có
. Lấy điểm
trên cạnh
sao cho
. Lấy điểm
trên cạnh
sao
. Giả sử
. Khi đó:
Độ dài cạnh là 2
Độ dài cạnh là 4
Ta có , theo định lý Thalès ta có:
Ta có:
Cho hình thang ![]() có
có ![]() . Một đường thẳng song song với hai đáy cắt các cạnh bên
. Một đường thẳng song song với hai đáy cắt các cạnh bên ![]() và
và ![]() theo thứ tự tại E và F (như hình vẽ). Tìm giá trị x.
theo thứ tự tại E và F (như hình vẽ). Tìm giá trị x.

Xét tam giác ACD có EK // CD, theo định lí Thalès nên
Xét tam giác ABC có AB // FK, theo định lí Thalès nên
Từ (1) và (2) suy ra
Cho hình thang ![]() có
có ![]() , hai đường chéo cắt nhau tại
, hai đường chéo cắt nhau tại ![]() . Tính độ dài
. Tính độ dài ![]() biết
biết ![]() .
.
Hình vẽ minh họa
Xét tam giác OCD có AB // CD
(hệ quả định lí Thalès)
Cho hình vẽ:

Tính giá trị của x.
Ta có:
Cho tam giác ![]() và trung tuyến
và trung tuyến ![]() . Một đường thẳng bất kỳ song song với AD cắt cạnh BC, đường thẳng
. Một đường thẳng bất kỳ song song với AD cắt cạnh BC, đường thẳng ![]() lần lượt tại
lần lượt tại ![]() . Tính giá trị biểu thức
. Tính giá trị biểu thức ![]() .
.
Hình vẽ minh họa
Trong tam giác có
Trong tam giác có
Mà BD = DC (AM là trung tuyến)
Cho tam giác ![]() , điểm
, điểm ![]() chia trong cạnh
chia trong cạnh ![]() theo tỉ số
theo tỉ số ![]() , điểm
, điểm ![]() chia trong
chia trong ![]() theo tỉ số
theo tỉ số ![]() . Gọi
. Gọi ![]() là giao điểm của
là giao điểm của ![]() và
và ![]() . Tính tỉ số
. Tính tỉ số ![]() ?
?
Kẻ ta có:
Tìm x trong hình vẽ:

Ta có:
Cho tam giác ABC, đường phân giác AD thỏa mãn ![]() . Tính số đo góc
. Tính số đo góc ![]() ?
?
Kẻ . Đặt
. Ta có
Theo bài ra ta có:
Suy ra
=> Tam giác ADE đều
Trong hình thang ![]() có
có ![]() , vẽ một đường thẳng song song với hai cạnh đáy, cắt
, vẽ một đường thẳng song song với hai cạnh đáy, cắt ![]() theo thứ tự ở
theo thứ tự ở ![]() và
và ![]() . Tính độ dài
. Tính độ dài ![]() biết rằng
biết rằng ![]() .
.
Hình vẽ minh họa
Theo giả thiết, vì nên
.
Gọi I là giao của AC và EF.
Áp dụng định lí Thalès cho tam giác ACD nên ta có:
Vì
Áp dụng định lí Thalès cho tam giác ABC ta có
Vậy
Cho tam giác ![]() có
có ![]() . Trên cạnh
. Trên cạnh ![]() lấy các điểm
lấy các điểm ![]() và
và ![]() sao cho
sao cho ![]() . Từ
. Từ ![]() và
và ![]() kẻ các đường thẳng song song với
kẻ các đường thẳng song song với ![]() , cắt
, cắt ![]() theo thứ tự tạo
theo thứ tự tạo ![]() và
và ![]() . Tính độ dài các cạnh
. Tính độ dài các cạnh ![]() và
và ![]() .
.
Hình vẽ minh họa
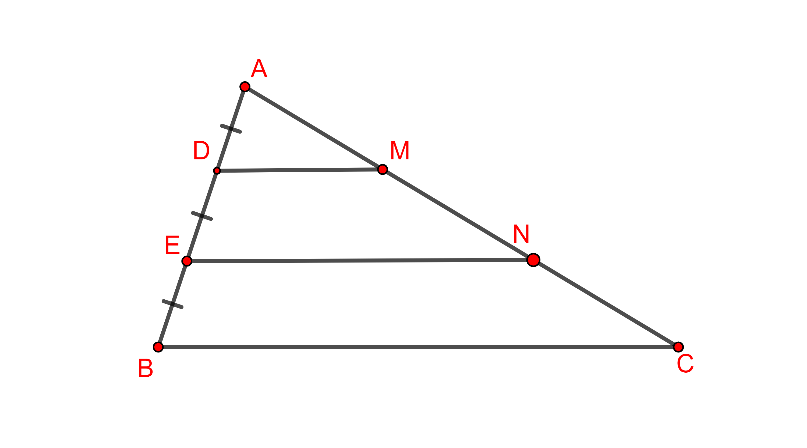
Xét tam giác có
=>
(theo Thalès)
Tương tự
