Luyện tập Hình chóp tứ giác đều KNTT

Nhận biết Thông hiểu Vận dụng

Bài kiểm tra này bao gồm 20 câu
Điểm số bài kiểm tra: 20 điểm
Xem lại kỹ lý thuyết trước khi làm bài
Chuẩn bị giấy và bút để nháp trước khi bắt đầu

Bắt đầu làm bài

00:00:00

Câu 1: Thông hiểu
Chọn đáp án chính xác
Một hình chóp tứ giác đều có chu vi đáy là 52cm, độ dài trung đoạn là 18cm. Nếu tăng kích thước mỗi cạnh đáy lên 2 lần và giữ nguyên độ dài trung đoạn thì diện tích xung quanh của hình chóp bằng bao nhiêu?
- A.
  932cm²
- B.
  857cm²
- C.
  914cm²
- D.
  824cm²
Hướng dẫn:
Cạnh đáy ban đầu có độ dài $52:4 = 13(cm)$

Độ dài cạnh đáy lúc sau: $13.2 = 26(cm)$

Diện tích xung quanh lúc sau: $S_{xq} = 2.26.18 = 936\left( cm^{2} ight)$
Câu 2: Thông hiểu
Chọn đáp án đúng
Nhân dịp Tết Trung Thu, Tuấn dự định làm một chiếc đèn lồng hình chóp tam giác đều và một chiếc hình chóp tứ giác đều. Mỗi chiếc lồng đền có độ dài cạnh đáy và đường cao của mặt bên tương ứng với đáy lần lượt là 45cm và 50cm. Hỏi Tuấn cần bao nhiêu mét vuông giấy vừa đủ để dán tất cả các mặt của mỗi chiếc đèn? (Coi các nếp gấp là không đáng kể).
- A.
  9854,12cm²
- B.
  10776,85cm²
- C.
  9254,54cm²
- D.
  10354,08cm²
Hướng dẫn:
Xét chiếc lồng đèn hình chóp tam giác đều:

Chiều cao mặt đáy là:

$\sqrt{45^{2} - \left( \frac{45}{2} ight)^{2}} = \frac{45\sqrt{3}}{2}(cm)$

Diện tích đáy chiếc đèn là:

$\frac{1}{2}.\frac{45\sqrt{3}}{2}.45 = \frac{2025\sqrt{3}}{4}\left( cm^{2} ight)$

Diện tích toàn phần chiếc đèn là:

$\frac{2025\sqrt{3}}{4} + 3.\frac{1}{2}.50.45 \approx 4251,85\left( cm^{2} ight)$

Xét chiếc lồng đèn hình chóp tứ giác đều:

Diện tích đáy chiếc đèn là:

$45^{2} = 2025\left( cm^{2} ight)$

Diện tích toàn phần chiếc đèn là:

$2025 + 2.45.50 = 6825\left( cm^{2} ight)$

Vậy diện tích giấy Tuấn cần dùng để làm 2 chiếc đèn là: 10776,85(cm²)
Câu 3: Nhận biết

Điền đáp án vào ô trống

Hình chóp tứ giác đều có độ dài cạnh đáy là $\sqrt{3}cm$ , độ dài trung đoạn gấp hai lần cạnh đáy. Tính tổng diện tích các mặt bên và mặt đáy?

Đáp án: 15cm²

Đáp án là:

Hình chóp tứ giác đều có độ dài cạnh đáy là $\sqrt{3}cm$ , độ dài trung đoạn gấp hai lần cạnh đáy. Tính tổng diện tích các mặt bên và mặt đáy?

Đáp án: 15cm²

Diện tích xung quanh hình chóp: $2.\sqrt{3}.2\sqrt{3} = 12cm^{2}$

Diện tích đáy là: $\left( \sqrt{3} ight)^{2} = 3cm^{2}$

Diện tích toàn phần là: $12 + 3 = 15\left( cm^{2} ight)$
Câu 4: Thông hiểu
Chọn đáp án đúng
Xác định công thức tính thể tích hình chóp tứ giác đều có chu vi đáy bằng a và chiều cao bằng h?
- A.
  $\frac{a^{2}h}{32}$
- B.
  $\frac{a^{2}h}{15}$
- C.
  $\frac{a^{2}h}{24}$
- D.
  $\frac{a^{2}h}{48}$
Hướng dẫn:
Độ dài cạnh đáy là $\frac{a}{4}$

Diện tích đáy là $\frac{a^{2}}{16}$

Thể tích hình chóp là $V = \frac{1}{3}.\frac{a^{2}}{16}.h = \frac{a^{2}h}{48}$
Câu 5: Thông hiểu

Điền đáp án vào ô trống

Tính thể tích của hình chóp tứ giác đều biết thể tích của hình chóp bằng một nửa thể tích của một hình lăng trụ đứng có đáy là hình vuông với cạnh là một số nguyên tố chẵn và có chiều cao lăng trụ là 27cm.

Đáp án: 54cm³

Đáp án là:

Tính thể tích của hình chóp tứ giác đều biết thể tích của hình chóp bằng một nửa thể tích của một hình lăng trụ đứng có đáy là hình vuông với cạnh là một số nguyên tố chẵn và có chiều cao lăng trụ là 27cm.

Đáp án: 54cm³

Số nguyên tố chẵn là 2

Vậy thể tích hình chóp là

$V_{c} = \frac{1}{2}V_{hlt} = \frac{2.2.27}{2} = 54\left( cm^{3} ight)$
Câu 6: Nhận biết
Tính chu vi đáy hình chóp
Diện tích xung quanh của hình chóp tứ giác đều bằng 1024cm², độ dài trung đoạn bằng 64cm. Hỏi chu vi đáy hình chóp bằng bao nhiêu?
- A.
  40cm
- B.
  24cm
- C.
  36cm
- D.
  32cm
Hướng dẫn:
Nửa chu vi đáy là: $\frac{1024}{64} = 16(cm)$

Chu vi đáy là: $16.2 = 32(cm)$
Câu 7: Thông hiểu

Ghi đáp án vào ô trống

Hình vẽ dưới đây mô tả một mô hình gồm hai phần: phần dưới có dạng hình lập phương cạnh 4,5cm, phần trên có dạng hình chóp tứ giác đều có chiều cao bằng 2cm. Tính thể tích mô hình?
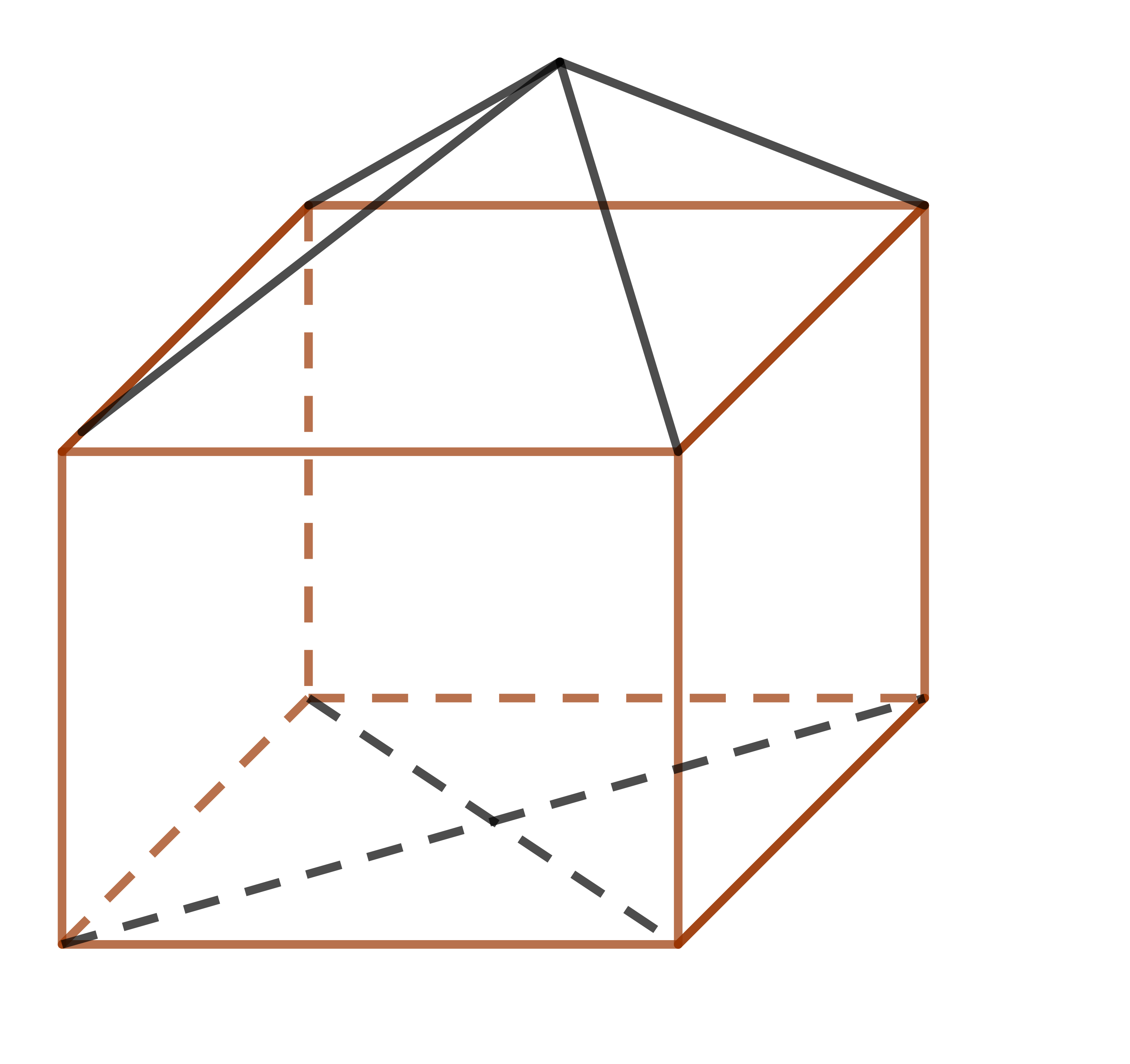
Đáp án: 104,625 cm³
(Đáp án ghi dưới dạng số thập phân)

Đáp án là:

Hình vẽ dưới đây mô tả một mô hình gồm hai phần: phần dưới có dạng hình lập phương cạnh 4,5cm, phần trên có dạng hình chóp tứ giác đều có chiều cao bằng 2cm. Tính thể tích mô hình?
Đáp án: 104,625 cm³
(Đáp án ghi dưới dạng số thập phân)

Thể tích hình chóp là: $V_{C} =\frac{1}{3}.2.4,5^{2} = 13,5$
Thể tích hình lập phương là: $V_{lp} =4,5^{3} = 91,125cm^{3}$
Vậy thể tích mô hình là 104,625cm³
Câu 8: Thông hiểu
Chọn đáp án đúng
Khi tăng kích thước mỗi cạnh đáy của một hình chóp tứ giác đều lên 3 lần và giữ nguyên chiều cao thì thể tích hình chóp mới gấp bao nhiêu lần thể tích ban đầu?
- A.
  4 lần
- B.
  8 lần
- C.
  9 lần
- D.
  6 lần
Hướng dẫn:
Thể tích hình chóp ban đầu là: $V_{1} = \frac{1}{3}a^{2}.h$

Thể tích hình chóp lúc sau là: $V_{2} = \frac{1}{3}(3a)^{2}.h = 9.\frac{1}{3}.a^{2}.h = 9V_{1}$

Vậy thể tích tăng gấp 9 lần.
Câu 9: Thông hiểu
Chọn khẳng định đúng
Một hình chóp tứ giác đều có cạnh đáy bằng a, chiều cao h. Nếu tăng cạnh đáy gấp 5 lần và tăng chiều cao gấp 3 lần thì khi đó thể tích sẽ thay đổi như thế nào?
- A.
  Tăng 75 lần so với thể tích ban đầu
- B.
  Tăng 25 lần so với thể tích ban đầu
- C.
  Tăng 45 lần so với thể tích ban đầu
- D.
  Tăng 15 lần so với thể tích ban đầu
Hướng dẫn:
Thể tích ban đầu là $V = \frac{1}{3}a^{2}.h$

Thể tích lúc sau là: $V' = \frac{1}{3}.(5a)^{2}.3h = 75.\frac{1}{3}a^{2}.h = 75V$

Vậy thể tích tăng gấp 75 lần so với ban đầu.
Câu 10: Thông hiểu
Tính thể tích và diện tích xung quanh hình chóp
Tìm diện tích xung quanh và thể tích của hình chóp tứ giác đều. Biết trung đoạn bằng 35cm, chiều cao hình chóp bằng 18cm và diện tích đáy bằng $144cm^{2}$ .
- A.
  $S_{xq} = 872cm^{2};V = 860cm^{3}$
- B.
  $S_{xq} = 860cm^{2};V = 872cm^{3}$
- C.
  $S_{xq} = 864cm^{2};V = 840cm^{3}$
- D.
  $S_{xq} = 840cm^{2};V = 864cm^{3}$
Hướng dẫn:
Cạnh đáy là: $\sqrt{144} = 12(cm)$

Chu vi đáy là $2.12 = 24(cm)$

Diện tích xung quanh là $S_{xq} = 24.35 = 840\left( cm^{2} ight)$

Thể tích hình chóp là $V = \frac{1}{3}.18.12^{2} = 864cm^{3}$
Câu 11: Nhận biết
Tính thể tích hình chóp
Hình chóp tứ giác đều có diện tích đáy là 16cm², chiều cao là 102dm. Tính thể tích của hình chóp.
- A.
  5440cm³
- B.
  544cm³
- C.
  5,44cm³
- D.
  54,4cm³
Hướng dẫn:
Thể tích hình chóp là: $\frac{1}{3}.16.1020 = 5440\left( cm^{3} ight)$
Câu 12: Thông hiểu
Xác định thể tích của hình chóp tứ giác
Diện tích xung quanh của một hình chóp tứ giác đều là 380cm², chiều cao là 14cm và trung đoạn bằng 32cm. Xác định thể tích của hình chóp tứ giác đều?
- A.
  $150,72cm^{3}$
- B.
  $162,34cm^{3}$
- C.
  $164,52cm^{3}$
- D.
  $156,14cm^{3}$
Hướng dẫn:
Nửa chu vi đáy là $\frac{380}{32} = 11,875(cm)$

Độ dài cạnh đáy là: $\frac{11,875.2}{4} = 5,9375(cm)$

Thể tích hình chóp là $V \approx 164,52\left( cm^{3} ight)$
Câu 13: Thông hiểu
Xác định diện tích xung quanh hình chóp
Cho hình chóp tứ giác đều có độ dài cạnh đáy bằng 10cm và độ dài cạnh bên là 6cm. Diện tích xung quanh hình chóp tứ giác là:
- A.
  $88,76cm^{2}$
- B.
  $122,14cm^{2}$
- C.
  $66,33cm^{2}$
- D.
  $48,32cm^{2}$
Hướng dẫn:
Mặt bên hình chóp tứ giác đều là tam giác cân cạnh bên bằng 6cm và cạnh đáy bằng 10cm.
=> Độ dài trung đoạn là $\sqrt{6^{2} -5^{2}} = \sqrt{11}(cm)$
Diện tích xung quanh hình chóp là:
$S_{xq} = 2.10.\sqrt{11} = 20\sqrt{11}\approx 66,33\left( cm^{2} ight)$
Câu 14: Thông hiểu

Điền kết quả vào ô trống

Xác định thể tích hình chóp tứ giác đều bằng một với thể tích của một hình lăng trụ đứng tứ giác. Biết lăng trụ có diện tích đáy bằng 36cm² và chiều cao bằng 22cm.

Đáp án: 792 cm³

Đáp án là:

Xác định thể tích hình chóp tứ giác đều bằng một với thể tích của một hình lăng trụ đứng tứ giác. Biết lăng trụ có diện tích đáy bằng 36cm² và chiều cao bằng 22cm.

Đáp án: 792 cm³

Thể tích hình chóp tứ giác đều là:

$V_{c} = V_{ltd} = 36.22 = 792\left( cm^{3} ight)$
Câu 15: Thông hiểu

Tính số tiền mua vải

Để may xung quanh một chiếc lều du lịch có dạng hình chóp tứ giác đều người ta dùng loại vải thô có giá 85000 đồng/m². Tính số tiền mua vải cần dùng để may lều biết độ dài cạnh đáy và trung đoạn của chiếc lều lần lượt dài 2,8m và 3m?

Kết quả: 1428000 đồng

Đáp án là:

Để may xung quanh một chiếc lều du lịch có dạng hình chóp tứ giác đều người ta dùng loại vải thô có giá 85000 đồng/m². Tính số tiền mua vải cần dùng để may lều biết độ dài cạnh đáy và trung đoạn của chiếc lều lần lượt dài 2,8m và 3m?

Kết quả: 1428000 đồng

Diện tích vải để may xung quanh chiếc lều là: $S_{xq} = 3.2.2,8 = 16,8\left( m^{2} ight)$

Số tiền cần dùng để mua vải là

$16,8.85000 = 1428000$ đồng.
Câu 16: Nhận biết
Tính chiều cao hình chóp
Hình chóp tứ giác đều có diện tích đáy là 25cm², thể tích là 150cm³. Tính chiều cao của hình chóp.
- A.
  20cm
- B.
  14cm
- C.
  22cm
- D.
  18cm
Hướng dẫn:
Chiều cao hình chóp là: $\frac{3.150}{25} = 18(cm)$
Câu 17: Nhận biết
Tính thể tích hình chóp
Cho hình chóp tứ giác đều S.EFKH như hình vẽ:
Biết cạnh đáy bằng 5cm và chiều cao hình chóp SO = 7cm?
- A.
  $175cm^{2}$
- B.
  $\frac{175}{2}cm^{2}$
- C.
  $\frac{175}{3}cm^{2}$
- D.
  $\frac{175}{6}cm^{2}$
Hướng dẫn:
Thể tích hình chóp là: $V =\frac{1}{3}.25.7 = \frac{175}{3}\left( cm^{3} ight)$
Câu 18: Nhận biết

Ghi đáp án đúng vào chỗ trống

Một khối đá dạng hình chóp tứ giác đều có độ dài cạnh đáy bằng 8cm và độ dài trung đoạn bằng 7cm. Tính diện tích xung quanh của khối đá?

Đáp án: 112 cm²

Đáp án là:

Một khối đá dạng hình chóp tứ giác đều có độ dài cạnh đáy bằng 8cm và độ dài trung đoạn bằng 7cm. Tính diện tích xung quanh của khối đá?

Đáp án: 112 cm²

Diện tích xung quanh của khối đá là:

$S_{xq} = 2.8.7 = 112\left( cm^{2} ight)$
Câu 19: Vận dụng
Tính thể tích hình chóp tứ giác
Một hình chóp tứ giác đều có diện tích một mặt bên bằng 64cm² và độ dài trung đoạn bằng 18cm. Tính thể tích hình chóp tứ giác đều gần nhất với kết quả nào dưới đây?
- A.
  $288cm^{3}$
- B.
  $297cm^{3}$
- C.
  $290cm^{3}$
- D.
  $276cm^{3}$
Hướng dẫn:
Độ dài cạnh đáy là $\frac{64.2}{18} = \frac{64}{9}(cm)$

Chiều cao của hình chóp là: $\sqrt{18^{2} - \left( \frac{1}{2}.\frac{64}{9} ight)^{2}} \approx 17,65(cm)$

Vậy thể tích hình chóp là:

$V = \frac{1}{3}.\left( \frac{64}{9} ight)^{2}.17,65 = 297,51\left( cm^{3} ight)$
Câu 20: Nhận biết
Chọn đáp án đúng
Hình chóp tứ giác đều S.QKAD có chiều cao bằng độ dài cạnh đáy bằng 10cm. Thể tích hình chóp S.QKA bằng bao nhiêu?
- A.
  $\frac{1000}{3}cm^{3}$
- B.
  $\frac{10000}{3}cm^{3}$
- C.
  $\frac{100}{3}cm^{3}$
- D.
  $100cm^{3}$
Hướng dẫn:
Diện tích đáy $10^{2} = 100\left( cm^{2} ight)$

Thể tích hình chóp là: $V = \frac{1}{3}.100.10 = \frac{1000}{3}\left( cm^{3} ight)$