Luyện tập Hình chữ nhật

Hình vẽ minh họa

Trong tam giác ACD, PQ là đường trung bình, suy ra .

Tương tự, .

Từ đó ta có và

Suy ra là hình bình hành.

Mặt khác, . Vậy là hình chữ nhật.

Hình vẽ minh họa

Theo giả thiết thì tứ giác có

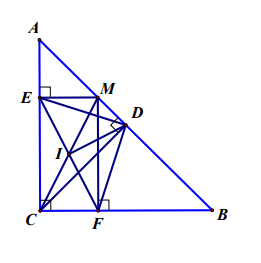
Do đó là hình chữ nhật.

Gọi I là giao điểm của EF và CM, I là trung điểm của EF và CM.

Vì tam giác ABC vuông cân tại C nên .

Xét tam giác DCM vuông tại D, có DI là trung tuyến nên:

Mà DI cũng là trung tuyến trong tam giác DEF, do vậy tam giác DEF vuông tại D.

Trong tứ giác CEDF có (1).

Dễ thấy (2) và (3) (tam giác BFM vuông cân tại F).

Từ (1), (2), (3) suy ra hai tam giác CED và BFD bằng nhau (g ‐ c ‐ g).

Từ đó, .

Vậy tam giác DEF vuông cân tại D.

Hình vẽ minh họa

Hai tam giác EBC và FBC là tam giác vuông tại E và F

M là trung điểm của BC

suy ra .

Vậy MEF là tam giác cân tại M.

Hình vẽ minh họa

Ta có O là trung điểm của AC và BD.

Mà ABCD là hình chữ nhật => BD = AC và OA = OB = OC = OD

Trong tam giác ABC, AM và BO là hai đường trung tuyến, do đó P là trọng tâm tam giác ABC.

Chứng minh tương tự ta suy ra Q là trọng tâm giác ADC

Mặt khác do đó O là trung điểm của PQ.

Vậy

Hình vẽ minh họa

 Dễ dàng chứng minh được OAMB là hình chữ nhật.

Ta có M là trung điểm của EF.

=> ME = MF = AB = MO, từ đó suy ra tam giác EOF vuông tại O.

Hình vẽ minh họa

Ta có:

Vì . Do đó ta có: . Kết hợp với giả thiết suy ra

(góc so le trong bằng nhau).

Mặt khác, (cùng vuông với AC), suy ra là hình bình hành.

Vì hình bình hành có một góc vuông nên là hình chữ nhật.

Vậy khẳng định sai là:

Hình chữ nhật là tứ giác có bốn góc vuông.

Hình vẽ minh họa

Tứ giác ADHK có ba góc vuông nên tứ giác ADHK là hình chữ nhật

Xét tam giác HBD có: nên tam giác HBD vuông cân

Đặt khi đó

Ta có:  không đổi

Dấu bằng xảy ra khi và chỉ khi hay D là trung điểm của BC

Vậy giá trị lớn nhất của DH.DK là

Hình vẽ minh họa

Ta có: (cùng phụ với góc ).

Tam giác ABC và BME là hai tam giác vuông có:

AC = BE

Dễ dàng chứng minh được ABMK là hình chữ nhật.

Do vậy tam giác KFE vuông cân tại K. Vậy .

Hình vẽ minh họa:

Ta có: ABCD là hình chữ nhật

Áp dụng định lí Pi – ta – go cho tam giác ABD ta có:

Áp dụng định lí Pi – ta – go cho tam giác AHD ta có:

(1)

Áp dụng định lí Pi – ta – go cho tam giác AHO ta có:

(2)

Từ (1) và (2) =>

Khẳng định sai là: “Tứ giác có hai đường chéo vuông góc với nhau là hình chữ nhật.”

Trong hình chữ nhật hai đường chéo bằng nhau và cắt nhau tại trung điểm do đó AC gấp đôi OC mà suy ra .

Hình vẽ minh họa

Ta có  (1).

Vì DMFN là hình chữ nhật nên (2)

Từ (1), (2) suy ra

Mặt khác theo giả thiết thì .

Vậy là hình bình hành.

Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.