Cho tam giác ![]() cân tại
cân tại ![]() , phân giác trong
, phân giác trong ![]() . Tính độ dài cạnh
. Tính độ dài cạnh ![]() biết
biết ![]()
![]() .
.
Hình vẽ minh họa
Ta có: là tia phân giác góc
nên
Theo tính chất của tỉ lệ thức ta có:
Ta có:
Cho tam giác ![]() cân tại
cân tại ![]() , phân giác trong
, phân giác trong ![]() . Tính độ dài cạnh
. Tính độ dài cạnh ![]() biết
biết ![]()
![]() .
.
Hình vẽ minh họa
Ta có: là tia phân giác góc
nên
Theo tính chất của tỉ lệ thức ta có:
Ta có:
Cho hình vẽ:

Tìm giá trị của x?
Ta có:
AM là phân giác góc BAC
Theo tính chất đường phân giác trong tam giác ta có:
Cho tam giác ![]() , đường phân giác của góc
, đường phân giác của góc ![]() cắt cạnh
cắt cạnh ![]() tại
tại ![]() . Tính tỉ số
. Tính tỉ số ![]() biết
biết ![]() .
.
Hình vẽ minh họa
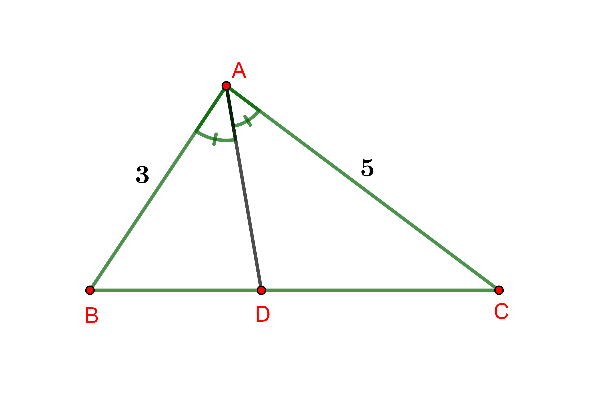
Ta có: AD là phân giác của ta có:
Vậy
Cho tam giác ![]() có đường phân giác
có đường phân giác ![]() . Tính độ dài đoạn
. Tính độ dài đoạn ![]() , biết
, biết ![]()
![]()
![]() ?
?
Hình vẽ minh họa
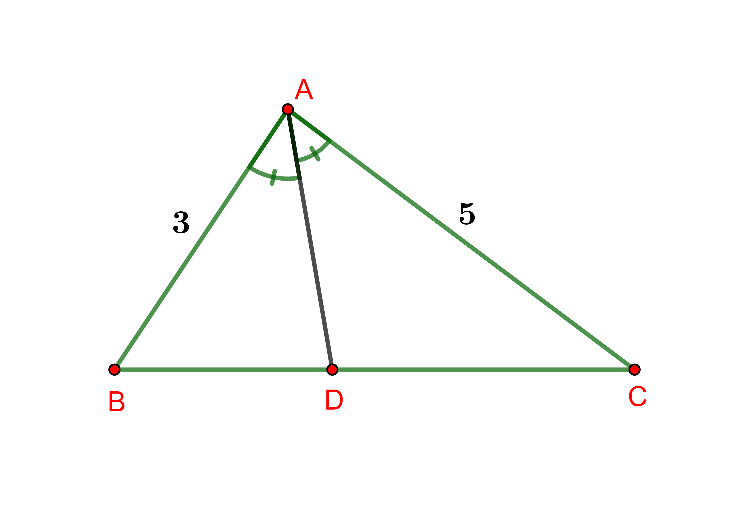
Ta có: AD là phân giác của ta có:
Tính giá trị y trong hình vẽ sau:

Xét ΔABC có AD là đường phân giác ngoài nên:
Mà 𝐵𝐵 là trung điểm của đoạn thẳng DC nên:
Từ (1) và (2)
Cho tam giác ![]() có các đường phân giác của
có các đường phân giác của ![]() . Biết chu vi tam giác
. Biết chu vi tam giác ![]() là
là ![]() và
và ![]() . Khi đó:
. Khi đó:
Độ dài cạnh ![]() là: 15
là: 15 ![]()
Độ dài cạnh ![]() là: 12
là: 12 ![]()
Độ dài cạnh ![]() là: 18
là: 18 ![]()
Cho tam giác có các đường phân giác của
. Biết chu vi tam giác
là
và
. Khi đó:
Độ dài cạnh là: 15
Độ dài cạnh là: 12
Độ dài cạnh là: 18
Hình vẽ minh họa:
Xét tam giác ABC có các đường phân giác BD và CE
Theo tính chất đường phân giác của tam giác ta có:
Từ (1) và (2)
Áp dụng tính chất dãy tỉ số bằng nhau ta được
Trong tam giác ![]() , đường phân giác
, đường phân giác ![]() chia cạnh đối diện thành các đoạn thẳng
chia cạnh đối diện thành các đoạn thẳng![]() . Đường trung trung trực của
. Đường trung trung trực của ![]() cắt đường thẳng
cắt đường thẳng ![]() ở
ở ![]() . Tính độ dài
. Tính độ dài ![]() .
.
Hình vẽ minh họa
Vẽ đường phân giác ngoài góc A cắt BC tại E. Ta có:
Suy ra
Vậy
Cho tam giác ![]() vuông tại
vuông tại ![]() ,
, ![]() là trung điểm của
là trung điểm của ![]() . Kẻ đường cao
. Kẻ đường cao ![]() và phân giác
và phân giác ![]() . Gọi
. Gọi ![]() là hình chiếu vuông góc của
là hình chiếu vuông góc của ![]() trên
trên ![]() . Tính độ dài
. Tính độ dài ![]() biết
biết ![]() .
.
Hình vẽ minh họa:
Ta có AK là phân giác góc A. Theo tính chất đường phân giác ta có:
Ta có: là hình chiếu vuông góc của
trên
suy ra
.
Theo định lí Talet ta có:
Cho tam giác ![]() có trọng tâm
có trọng tâm ![]() . Gọi
. Gọi ![]() là giao điểm ba đường phân giác trong của tam giác ABC. Giả sử
là giao điểm ba đường phân giác trong của tam giác ABC. Giả sử ![]() . Khi đó:
. Khi đó:
![]() 2
2 ![]()
Cho tam giác có trọng tâm
. Gọi
là giao điểm ba đường phân giác trong của tam giác ABC. Giả sử
. Khi đó:
2
Theo tính chất đường phân giác trong tam giác và tam giác
ta có:
Theo bài ra ta có: khi đó
Hay
Cho tam giác ![]() có các đường phân giác
có các đường phân giác ![]() . Biết
. Biết ![]() . Tỉ số diện tích hai tam giác
. Tỉ số diện tích hai tam giác ![]() và tam giác
và tam giác ![]() bằng bao nhiêu?
bằng bao nhiêu?
Hình vẽ minh họa
Ta có:
Xét tam giác ABC có AD là phân giác góc A
Theo tính chất đường phân giác trong tam giác ta có:
Gọi là chiều cao từ đỉnh A đến đáy BC khi đó ta có:
Cho tam giác ![]() vuông tại
vuông tại ![]() , đường cao
, đường cao ![]() . Tia phân giác của góc
. Tia phân giác của góc ![]() cắt
cắt ![]() tại
tại ![]() , tia phân giác góc
, tia phân giác góc ![]() cắt
cắt ![]() tại
tại ![]() . Biết
. Biết ![]() và chu vi tam giác
và chu vi tam giác ![]() bằng
bằng ![]() . Khi đó:
. Khi đó:
Độ dài cạnh ![]() là: 25
là: 25
Độ dài cạnh ![]() là: 12
là: 12
Độ dài cạnh ![]() là: 4
là: 4
Độ dài cạnh ![]() là: 6
là: 6
Cho tam giác vuông tại
, đường cao
. Tia phân giác của góc
cắt
tại
, tia phân giác góc
cắt
tại
. Biết
và chu vi tam giác
bằng
. Khi đó:
Độ dài cạnh là: 25
Độ dài cạnh là: 12
Độ dài cạnh là: 4
Độ dài cạnh là: 6
Hình vẽ minh họa:
Ta có chu vi tam giác ABC bằng
Ta có:
Xét tam giác ABH có AD là phân giác góc BAH
Xét tam giác ACH có AE là phân giác góc HAC
Cho tam giác ![]() , hai đường phân giác
, hai đường phân giác ![]() cắt nhau tại
cắt nhau tại ![]() . Biết
. Biết ![]()
![]() . Tính độ dài cạnh
. Tính độ dài cạnh ![]() .
.
Hình vẽ minh họa
Xét tam giác AEC có CO là phân giác góc ACE khi đó
Xét tam giác ABC có CD là phân giác góc ACB khi đó:
Ta có:
Xét tam giác ABC có AE là phân giác góc BAC khi đó:
Cho tam giác ![]() có ba phân giác
có ba phân giác ![]() cắt nhau tại
cắt nhau tại ![]() . Khi đó tính giá trị của tích
. Khi đó tính giá trị của tích ![]() bằng bao nhiêu?
bằng bao nhiêu?
Hình vẽ minh họa
Ta có là phân giác góc A.
Theo tính chất đường phân giác trong tam giác ta có:
Tương tự đối với các đường phân giác ta có:
Do đó:
Xác định giá trị của x trong hình vẽ

Làm tròn kết quả đến chữ số thập phân thứ nhất.
Ta có:
AD là phân giác góc BAC
Theo tính chất đường phân giác trong tam giác ta có:
Cho tam giác ![]() vuông cân tại
vuông cân tại ![]() . Đường cao
. Đường cao ![]() và đường phân giác
và đường phân giác ![]() cắt nhau tại
cắt nhau tại ![]() . Tỉ số
. Tỉ số ![]() bằng:
bằng:
Hình vẽ minh họa
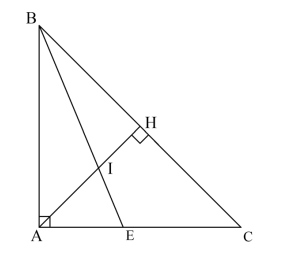
Ta có:
Suy ra tam giác AIE cân tại A =>
Áp dụng tính chất đường phân giác cho tam giác ABH và BAC ta có:
Từ (1), (2) và (3)
Vì tam giác ABC vuông cân kết hợp với (4) suy ra
Hay
