Hình chữ nhật có …….… là hình vuông.
Hình chữ nhật có hai đường chéo vuông góc là hình vuông.
Cho hình thoi 
có góc là góc tù. Biết đường cao kẻ từ đỉnh đến cạnh chia đôi cạnh đó. Tính số đo góc .
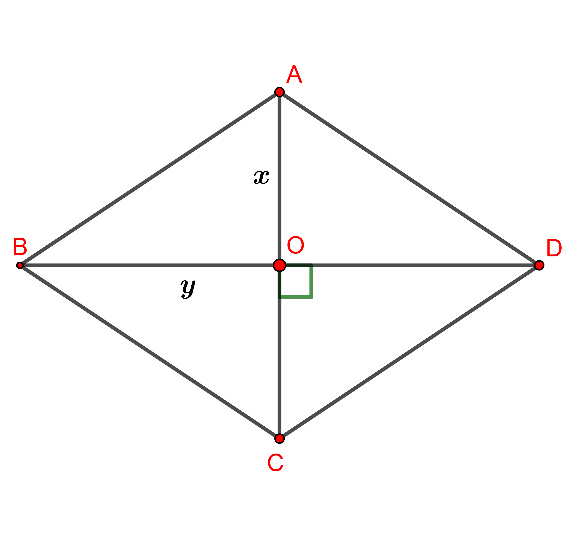
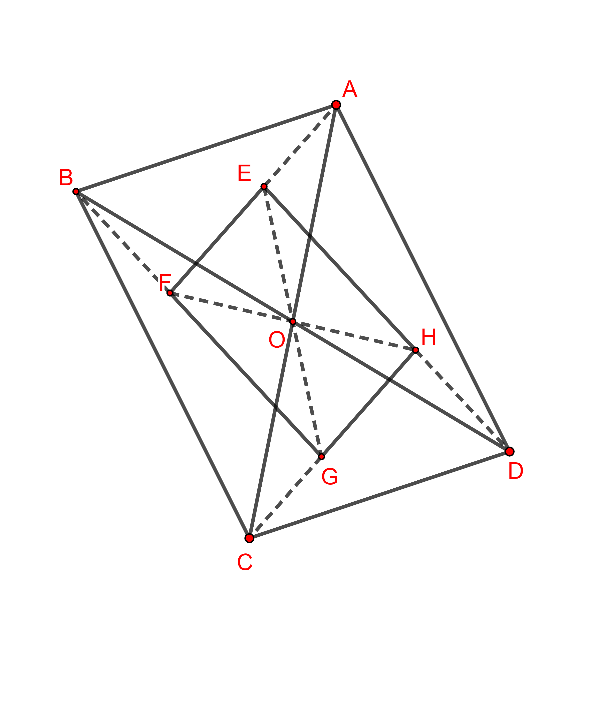
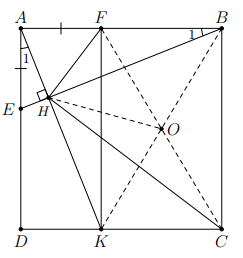
Hình vẽ minh họa
Gọi là chân đường cao kẻ từ
đến cạnh
và từ giả thiết ta có:
Ta có: =>
là đường trung trực của
nên
Áp dụng định nghĩa hình thoi nên tam giác
là tam giác đều do đó
Vì góc và góc
là hai góc trong cùng phía của
nên chúng bù nhau hay
Cho hình vuông . Lấy các điểm lần lượt thuộc các cạnh sao cho . Qua kẻ đường thẳng vuông góc với cắt tại . Tứ giác là hình gì?
Hình vẽ minh họa
Vẽ ME ⊥ CD, NF ⊥ AD.
Gọi O là giao điểm của ME và NF.
Ta có: mà
nên
Dễ thấy tứ giác AMOF là hình vuông.
Xét ∆EMP và ∆FNQ có:
(hai góc có cạnh tương ứng vuông góc)
Ta có:
Các tam giác bằng nhau nên suy ra
Do đó tứ giác MNPQ là hình thoi. Mà hình thoi có hai đường chéo bằng nhau nên MNPQ là hình vuông.
Cho hình thoi có . Điểm M là trung điểm cạnh AB. Kẻ . Số đo góc bằng bao nhiêu?
Hình vẽ minh họa:
Gọi trung điểm cạnh CD là N
Ta có và
nên tứ giác AMCN là hình bình hành
Mặt khác tại K
Xét tam giác HCD có và
nên
Xét tam giác HAD có KA vừa là đường cao vừa là đường trung tuyến nên tam giác HAD cân
Mặt khác nên
=> Tam giác ABH cân
Xét tứ giác ABHD có:
Mặt khác
Cho hình bình hành , hai đường chéo cắt nhau tại O. Gọi lần lượt là giao điểm các đường phân giác . Khi đó tứ giác EFGH là hình gì?
Hình vẽ minh họa
Ta có: (hai tia phân giác của hai góc kề bù)
=> thẳng hàng
Chứng minh tương tự ta được thẳng hàng
Ta có:
(một nửa của hai góc bằng nhau)
Chứng minh tương tự ta được
Tứ giác EFGH có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành. Hình bình hành có hai đường chéo vuông góc nên là hình thoi.
Trong các hình sau các hình nào có hai đường chéo cắt nhau tại trung điểm mỗi đường:
Trong các hình thoi, hình bình hành, hình chữ nhật đều có hai đường chéo cắt nhau tại trung điểm mỗi đường trừ hình thang cân không có nên “Hình chữ nhật và hình bình hành, hình thoi.” ĐÚNG.
Tứ giác nào sau đây vừa là hình chữ nhật, vừa là hình thoi?
Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.
Hình vuông là hình thoi có một góc vuông.
Vậy hình vuông vừa là hình chữ nhật, vừa là hình thoi.
Cho hình vuông . Trên cạnh AC lấy các điểm E và F sao cho . Trên cạnh lấy điểm sao cho . Tính tổng số đo các góc .
Hình vẽ minh họa
Các tứ giác là hình bình hành nên
Suy ra
Do đó:
Cho hình bình hành có vuông góc với . Trung điểm của các cạnh lần lượt là . Khi đó tứ giác là:
Hình vẽ minh họa
Ta có: ABCD là hình bình hành
=> AD // BC; AB = CD (1)
Mà
Xét tam giác ACD vuông tại A có F là trung điểm của CD
=> (2)
Xét tam giác ABC vuông tại C có E là trung điểm của AB => (3)
=> AE = EC = CF = FA
=> AECF là hình thoi.
Một hình vuông có cạnh bằng 4cm thì độ dài đường chéo hình vuông đó sẽ là:
Hình vẽ minh họa
Ta có ABCD là hình vuông => Tam giác ABC vuông cân tại B
Áp dụng định lí Pythagore cho tam giác ABC vuông cân tại B ta có:
Cho hình thoi có chu vi bằng . Tính giá trị lớn nhất của tích hai đường chéo hai hình thoi.
Hình vẽ minh họa:
Gọi O là giao điểm của hai đường chéo
Đặt
Ta có:
Từ bất đẳng thức
Do đó
Giá trị lớn nhất của tích hai đường chéo là 8 khi
Hay
Vậy là hình vuông thì tích hai đường chéo lớn nhất.
Cho hình vuông . Lấy các điểm theo thứ tự thuộc các cạnh sao cho . Gọi là hình chiếu của trên . Tính số đo góc .
Hình vẽ minh họa
Gọi là giao điểm của
và
⇒ là hình chữ nhật
Gọi là tâm hình chữ nhật
Xét tam giác vuông tại
nên
Tam giác vuông tại
Vậy
Độ dài hai đường chéo hình thoi lần lượt là . Khi đó độ dài cạnh hình thoi là:
Hình vẽ minh họa
ABCD là hình thoi => Hai đường chéo vuông góc và cắt nhau tại trung điểm mối đường
Hay . Áp dụng định lí Pythagore cho tam giác OAB vuông tại O ta có:
Câu nào đúng trong các câu sau:
Trong hình thoi: Hai đường chéo vuông góc với nhau.
Hình thoi có …….…... là hình vuông.
Hình thoi có hai đường chéo bằng nhau là hình vuông.
