Hình thang 
có . Tính số đo góc của hình thang?
Ta có: ABCD là hình thang suy ra:
Cho tam giác ABC có BC = a, các đường trung tuyến BD, CE. Lấy các điểm M, N trên cạnh BC sao cho BM = MN = NC. Gọi I là giao điểm của AM và BD, K là giao điểm của AN và CE. Tính độ dài IK.
Hình vẽ minh họa
Dễ thấy DN là đường trung bình của ACM nên DN // AN.
Xét tam giác BND có
BM = MN
MI // ND
=> I là trung điểm của BD.
Tương tự K là trung điểm của CE.
Hình thang BEDC có I và K là trung điểm của hai đường chéo nên dễ dàng chứng minh được:
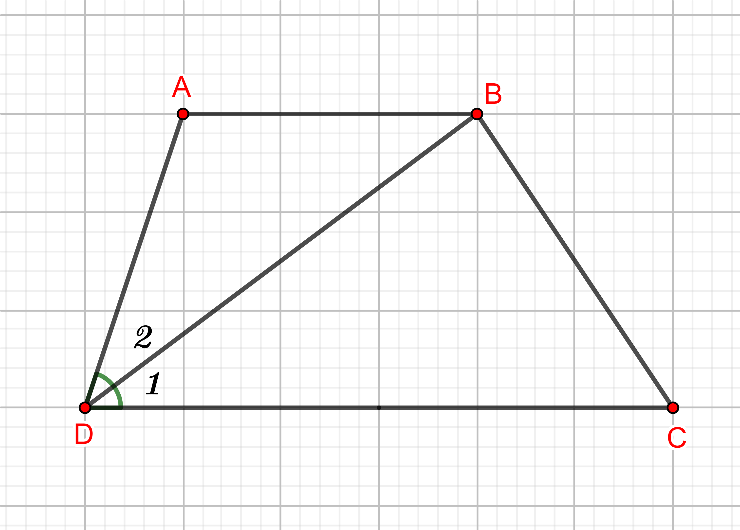
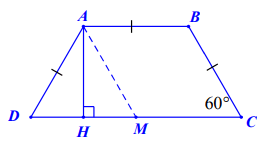
Cho hình thang có và . Tính số đo góc .
Hình vẽ minh họa
Hình vẽ minh họa
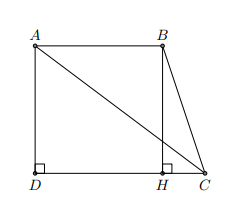
Kẻ BE⊥ CD thì AD // BE do cùng vuông góc với CD nên hình thang ABED có hai cạnh bên song song
Áp dụng nhận xét về hình thang có hai cạnh bên song song vào hình thang ABED và giả thiết ta được:
Do đó
Suy ra ∆BEC vuông cân tại E nên
Do đó góc B và C là hai góc trong cùng phía của AB // DC nên chúng bù nhau.
Cho hình thang cân có đáy lớn , cạnh bên dài , góc . Kẻ . Khi đó độ dài cạnh AB là:
Hình vẽ minh họa
Kẻ
Suy ra tam giác AED là tam giác đều
Hình thang ABCD có , đáy nhỏ . Tính độ dài AC.
Hình vẽ minh họa
Kẻ BH ⊥ CD.
Ta tính được CH = 5 cm, CD = 16 cm. Từ đó AC = 20 cm.
Hình thang có . Tính số đo góc ?
Ta có: ABCD là hình thang suy ra:
Cho hình thang cân có và là tia phân giác của góc . Chọn đáp án đúng?
Hình vẽ minh họa:
Vì ABCD là hình thang cân nên
Mà DB là tia phân giác của góc D nên
Xét tam giác BDC có:
Một hình thang cân có đáy nhỏ bằng cạnh bên và góc kề với đáy lớn bằng 60°. Biết chiều cao của hình thang cân này là . Tính chu vi của hình thang cân.
Hình vẽ minh họa
Ta đặt
Vẽ , ta được
và
Ta lại có cân có
nên là tam giác đều, suy ra:
.
Vẽ thì
là đường cao của hình thang cân, cũng là đường cao của tam giác đều:
vì
Do đó chu vi của hình thang cân là:
Cho hình thang ABCD có và . Độ dài cạnh BC là:
Hình vẽ minh họa
Kẻ BH⊥CD. Hình thang ABHD có AD//BH, nên:
Tam giác BHC vuông tại H, theo định lí pytago ta có:
Cho tam giác , trọng tâm . Vẽ đường thẳng đi qua , cắt các đoạn thẳng . Gọi là hình chiếu của trên . Nếu đường thẳng nằm ngoài tam giác ABC và G’ là hình chiếu của trên thì các độ dài có liên hệ gì?
Hình vẽ minh họa
Gọi là đường trung tuyến của tam giác
, M là trung điểm của
.
Vẽ vuông góc với
.
Ta có
Cho hình thang cân có . Số đo góc D của hình thang là:
Hình vẽ minh họa
Ta có ∆ABC cân tại B khi đó
Tương tự ta chứng minh được
Ta lại có:
Cho hình thang cân ABCD có AB // CD, đường chéo DB vuông góc với cạnh bên BC, DB là tia phân giác góc D. Tính chu vi của hình thang, biết BC = 3 cm.
Hình vẽ minh họa
Trong hình thang cân ABCD có:
Gọi => Tam giác OCD đều nên
=> Tam giác OAB đều
Chu vi của hình thang ABCD là .
Trong các hình sau các hình nào là hình thang:
Hình 1, 4 là các hình thang vì có hai cạnh đối song song.
Cho hình thang cân có thì:
Trong hình thang cân hai góc ở đáy bằng nhau mà hình thang cân có
do đó
.
Cho hình thang cân có . Hỏi số đo các góc bằng bao nhiêu?
Vì ABCD là hình thang cân nên
