Cho hình bình hành ![]() có hai đường chéo
có hai đường chéo ![]() và
và ![]() cắt nhau tại
cắt nhau tại ![]() . Tính độ dài đoạn
. Tính độ dài đoạn ![]() biết
biết ![]() .
.
Trong hình bình hành hai đường chéo cắt nhau tại trung điểm do đó bằng
mà
suy ra
Vậy .
Cho hình bình hành ![]() có hai đường chéo
có hai đường chéo ![]() và
và ![]() cắt nhau tại
cắt nhau tại ![]() . Tính độ dài đoạn
. Tính độ dài đoạn ![]() biết
biết ![]() .
.
Trong hình bình hành hai đường chéo cắt nhau tại trung điểm do đó bằng
mà
suy ra
Vậy .
Cho tam giác ABC, các đường cao BH và CK cắt nhau tại E. Đường thẳng qua B vuông góc với AB và đường thẳng qua C vuông góc với AC cắt nhau tại D. Gọi M là trung điểm của BC. Tứ giác BDCE là hình gì?
Hình vẽ minh họa
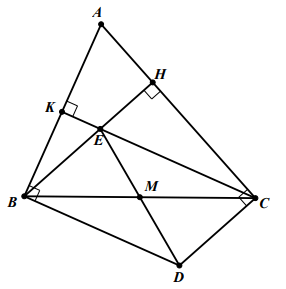
Ta có:
Từ (*) và (**) suy ra BDCE là hình bình hành.
Cho điểm E thuộc cạnh AC của tam giác đều ABC. Đường vuông góc với AB kẻ từ E cắt đường vuông góc với BC kẻ từ C tại điểm D. Gọi K là trung điểm của AE. Tính số đo góc ![]() ?
?
Hình vẽ minh họa:
Vẽ F sao cho K là trung điểm của DF thì AF // DE, AF = DE.
Tam giác DEC có nên DE = DC, suy ra AF = DC.
∆BAF = ∆BCD (c – g - c) nên BF = BD, .
Ta lại có , do đó ∆DBF đều
Cho hình bình hành ![]() có
có ![]() thì
thì
Trong hình bình hành các cạnh đối bằng nhau mà hình bình hành ABCD có AB = 2cm nên
Cho hình bình hành![]() có
có ![]() . Khi đó
. Khi đó ![]() bằng bao nhiêu?
bằng bao nhiêu?
Trong hình bình hành ABCD có là hai góc đối nhau mà các góc đối của hình bình hành thì bằng nhau do đó
mà
suy ra
.
Cho tam giác ABC, trực tâm H. Gọi M là trung điểm của BC, N là trung điểm của AC. Đường vuông góc với BC tại M và đường vuông góc với AC tại N cắt nhau ở O. Trên tia đối của tia OC, lấy điểm K sao cho OK = OC. Tính tỉ số ![]() bằng bao nhiêu?
bằng bao nhiêu?
Hình vẽ minh họa
Tam giác KBC có KO = OC, BM = MC nên OM là đường trung bình của ∆KBC.
Suy ra OM // KB, .
Ta lại có OM // AH (cùng vuông góc với BC).
Suy ra KB // AH.
Chứng minh tương tự ta có: KA // BH.
Tứ giác AHBK có KB // AH, KA // BH nên là hình bình hành.
Ta có: AHBK là hình bình hành nên KB = AH
Ta lại có:
Cho tứ giác ![]() có
có ![]() và
và ![]() .
.
(1) Tia DB là tia phân giác của góc D.
(2) Tứ giác ![]() là hình thang cân.
là hình thang cân.
(3) Tứ giác ![]() là hình bình hành.
là hình bình hành.
(4) Tứ giác ![]() là hình thang vuông.
là hình thang vuông.
Trong các khẳng định sau có bao nhiêu kết quả sai?
Hình vẽ minh họa:
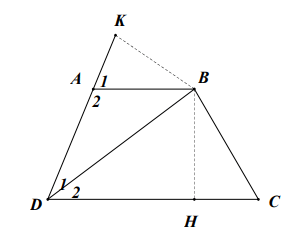
Vẽ
Ta có: (cùng bù với
).
Từ đó suy ra
Suy ra DB là tia phân giác của góc D.
Góc là góc ngoài tại đỉnh A của tam giác cân ADB, nên
(vì có cặp góc đồng vị bằng nhau).
Vậy tứ giác ABCD là hình thang. Hình thang này có (vì cùng bằng
) nên là hình thang cân.
Vậy có 2 khẳng định sai.
Trong các hình sau các hình nào có các cạnh đối song song và bằng nhau:
Trong các hình: hình bình hành, hình chữ nhật đều có các cạnh đối song song và bằng nhau
Hình thang cân chỉ có 1 cặp cạnh đối song song nên không thỏa mãn.
Điền cụm từ thích hợp vào chỗ trống: “Trong hình bình hành hai đường chéo cắt nhau …”
Trong hình bình hành hai đường chéo cắt nhau tại trung điểm mỗi đường.
Cho tam giác đều ABC, một đường thẳng song song với BC cắt AB, AC ở D và E. Gọi G là trọng tâm của tam giác ADE, I là trung điểm của CD. Tính số đo góc ![]() ?
?
Hình vẽ minh họa:
Qua C vẽ đường thẳng song song với BD, cắt DE ở K.
Ta có BDKC là hình bình hành nên B, I, K thẳng hàng.
=> ∆GDB = ∆GEK (c – g - c) nên GB = GK
Suy ra ∆GBK cân tại G có
Cho hình bình hành ABCD có ![]() , phân giác góc D đi qua trung điểm của cạnh AB. Khi đó tỉ số
, phân giác góc D đi qua trung điểm của cạnh AB. Khi đó tỉ số ![]() là bao nhiêu?
là bao nhiêu?
Hình vẽ minh họa
Gọi M là trung điểm của cạnh AB, ta có (1) (so le trong).
Mặt khác, DM là phân giác góc D nên (2)
Từ (1), (2) suy ra
Do đó tam giác ADM cân tại A.
Vậy
Cho tứ giác ![]() . Gọi
. Gọi ![]() lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh ![]() . Khi đó tứ giác
. Khi đó tứ giác ![]() là hình gì?
là hình gì?
Hình vẽ minh họa:
Xét tam giác DAC có PQ là đường trung bình
Xét tam giác BAC có MN là đường trung bình
Từ (1) và (2) suy ra
Tứ giác là hình bình hành.
Cho hình thang cân ABCD (AB//CD, AB < CD). Trên tia đối của tia BA lấy điểm E sao cho CB = CE. Khi đó tứ giác AECD là hình gì?
Hình vẽ minh họa
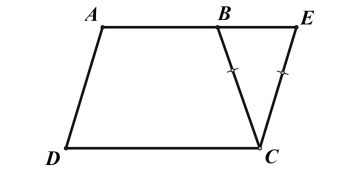
Dễ thấy tam giác BCE cân tại C suy ra
Ta lại có
Mà nên
Suy ra AC // ED (2 góc trong cùng phía bù nhau)
Suy ra AECD là hình bình hành.
Cho hình bình hành ABCD có ![]() , phân giác góc D đi qua trung điểm của cạnh AB. Lấy E là trung điểm của CD. Tam giác ACE là tam giác gì?
, phân giác góc D đi qua trung điểm của cạnh AB. Lấy E là trung điểm của CD. Tam giác ACE là tam giác gì?
Hình vẽ minh họa
Trong hình bình hành ABCD, và
.
Tam giác ADE cân và có một góc bằng , nên tam giác ADE đều.
Theo trên, tâm giác ADE đều nên , suy ra tam giác AEC cân tại E.
Cho tam giác ABC, các đường cao AK và BD cắt nhau tại G. Vẽ các đường trung trực HE, HF của các cạnh AC, BC. Đường thẳng qua A song song với BG cắt đường thẳng qua B song song với AK tại I. Chọn đáp án đúng.
Hình vẽ minh họa:
Ta có AG // BI và BG // AI nên tứ giác AIBG là hình bình hành, suy ra BG // AI; BG = AI
IB // AG ⇒ IB ⊥ BC mà HF⊥ BC, do đó IB // HF.
Lại có F là trung điểm của BC nên HF đi qua trung điểm của IC.
Chứng minh tương tự, HE cũng đi qua trung điểm của IC.
Từ đó ta được H là trung điểm của IC
Trong ∆AIC có: HE là đường trung bình, do đó
Vậy
