Lớp 11 Toán 11 (sách cũ)

Luyện tập Hai đường thẳng vuông góc

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 12 câu
  • Điểm số bài kiểm tra: 12 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Vận dụng
    Xác định góc giữa hai vectơ

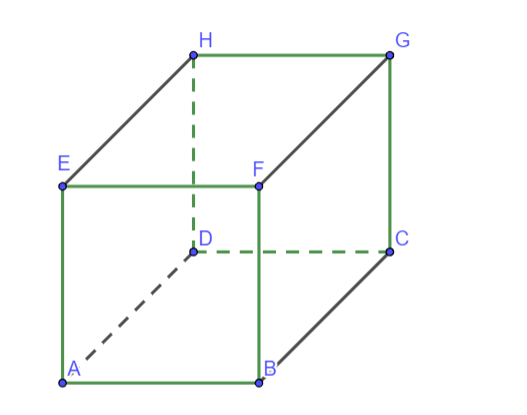
    Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vecto \overrightarrow {AB} và \overrightarrow {DH}?

    Hướng dẫn:

    Hình vẽ minh họa

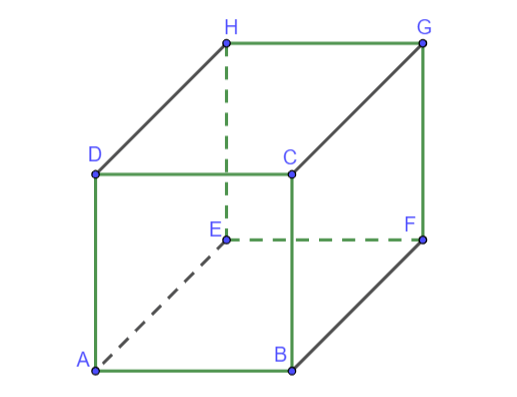
    Xác định góc giữa hai vectơ

    Ta có:

    \begin{matrix} \left\{ \begin{gathered} AB \bot AE \hfill \\ AE//DH \hfill \\ \end{gathered} ight. = > AB \bot DH \hfill \\ \Rightarrow \widehat {\left( {AB,DH} ight)} = {90^0} \hfill \\ \end{matrix}

  • Câu 2: Thông hiểu
    Hãy xác định góc giữa cặp vecto

    Cho hình lâp phương ABCD.EFGH. Hãy xác định góc giữa cặp vecto \overrightarrow {AB} và \overrightarrow {EG}?

    Hướng dẫn:

    Hình vẽ minh họa

    Hãy xác định góc giữa cặp vecto

    Ta có: AEGC là hình chữ nhật nên EG // AC

    Vì ABCD là hình vuông nên

    => \left( {\overrightarrow {AB} ,\overrightarrow {EG} } ight) = \left( {\overrightarrow {AB} ;\overrightarrow {AC} } ight) = \widehat {BAC} = {45^0}

  • Câu 3: Vận dụng
    Tìm bước giải sai của bài toán

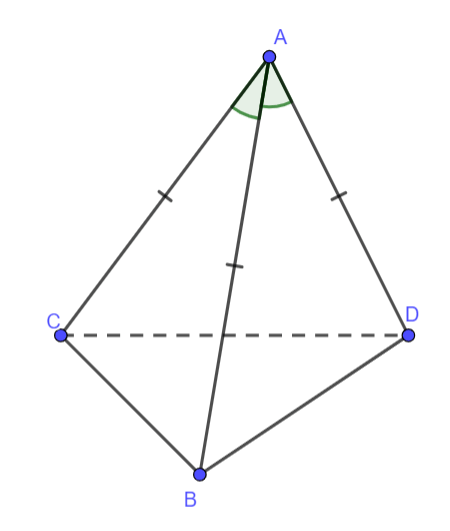
    Cho tứ diện ABCD có AB = AC = AD, \widehat {BAC} = \widehat {BAD} = {60^0}. Hãy chứng mình AB ⊥ CD.

    Một bạn chứng mình qua các bước sau:

    Bước 1. \overrightarrow {CD} = \overrightarrow {AC} - \overrightarrow {AD}

    Bước 2. \overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AB} .\left( {\overrightarrow {AC} - \overrightarrow {AD} } ight)

    Bước 3. \overrightarrow {AB} .\overrightarrow {AC} - \overrightarrow {AB} .\overrightarrow {AD} = |\overrightarrow {AB} |.|\overrightarrow {AD} |.\cos {60^0} - |\overrightarrow {AB} |.|\overrightarrow {AD} |.\cos {60^0} = 0

    Bước 4. Suy ra AB ⊥ CD

    Theo em. Lời giải trên sai từ:

    Hướng dẫn:

    Bài toán sai từ bước 1 vì

    Theo quy tắc trừ hai vectơ ta có:

    \overrightarrow {CD} = \overrightarrow {AD} - \overrightarrow {AC} {\text{ }}

  • Câu 4: Vận dụng
    Hoàn thành mệnh đề

    Cho vecto \vec{n} ≠ \vec{0} và hai vecto \vec{a} và \vec{b} không cùng phương. Nếu vecto \vec{n} vuông góc với cả hai vecto \vec{a} và \vec{b} thì \vec{n} , \vec{a} và \vec{b}:

    Hướng dẫn:

    Trường hợp "Đồng phẳng" và " Có thể đồng phẳng" sai vì có thể xảy ra trường hợp như hình vẽ sau:

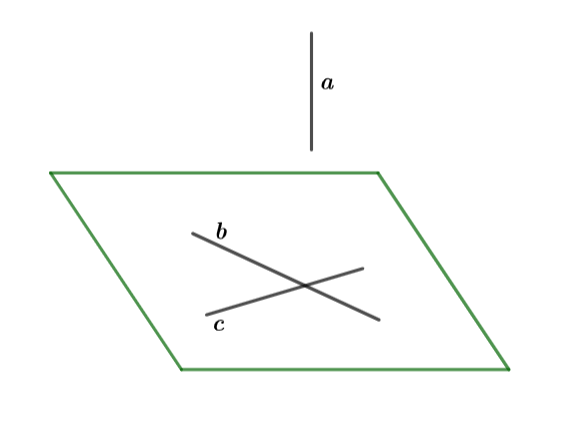
    Hoàn thành mệnh đề

    Giả sử trường hợp "Không đồng phẳng" sai tức là ba vecto  \vec{n} , \vec{a} và \vec{b} đồng phẳng. 

    Khi đó vì \left\{ {\begin{array}{*{20}{c}} {\overrightarrow n \bot \overrightarrow a } \\ {\overrightarrow n \bot \overrightarrow b } \end{array}} ight. \Rightarrow \overrightarrow a //\overrightarrow bđiều này mẫu thuẫn với giả thiết hai vecto  \vec{a} và \vec{b} không cùng phương.

    Vậy đáp án đúng là "Không đồng phẳng"

  • Câu 5: Thông hiểu
    Hoàn thành mệnh đề

    Cho ba vecto \vec{n}, \vec{a}, \vec{b} bất kì đều khác với vecto \vec{0}. Nếu vecto \vec{n} vuông góc với cả hai vecto \vec{a} và \vec{b} thì \vec{n}, \vec{a} và \vec{b}:

    Hướng dẫn:

    Nếu vecto \vec{n} vuông góc với cả hai vecto \vec{a} và \vec{b} thì \vec{n}, \vec{a} và \vec{b} thì có thể đồng phẳng.

  • Câu 6: Thông hiểu
    Hoàn thành mệnh đề

    Nếu ba vecto \vec{a}, \vec{b}, \vec{c} cùng vuông góc với vecto \vec{n} khác \vec{0} thì chúng: 

    Hướng dẫn:

    "Nếu ba vecto \vec{a}, \vec{b}, \vec{c} cùng vuông góc với vecto \vec{n} khác \vec{0} thì chúng đồng phẳng"

    Giải thích:

    Giả sử \vec{a}, \vec{b}, \vec{c} không đồng phẳng, khi đó tồn tại duy nhất bộ số thực (x; y; z) sao cho:

    \overrightarrow n = x\overrightarrow a + y\overrightarrow b + z\overrightarrow c

    Nhân cả hai vế với \overrightarrow n ta có:

    \begin{matrix} \overrightarrow n .\overrightarrow n = x\overrightarrow a .\overrightarrow n + y\overrightarrow b .\overrightarrow n + z\overrightarrow c .\overrightarrow n = 0 \hfill \\ \Rightarrow \overrightarrow n = \overrightarrow 0 \hfill \\ \end{matrix} 

    (Mâu thuẫn với giả thiết)

  • Câu 7: Thông hiểu
    Hoàn thành mệnh đề

    Các đường thẳng cùng vuông góc với một đường thẳng thì:

    Hướng dẫn:

    Đáp án "Thuộc một mặt phẳng" sai vì có thể xảy ra trường hợp nằm trên nhiều mặt phẳng khác nhau.

    Đáp án "Vuông góc với nhau" sai vì có thể xảy ra trường hợp chúng song song với nhau.

    Đáp án "Song song với nhau" sai vì có thể xảy ra trường hợp chúng cắt nhau.

    Đáp án "Song song với một mặt phẳng" đúng vì chúng đồng phẳng.

  • Câu 8: Thông hiểu
    Cặp đường thẳng nào sau đây không vuông góc với nhau

    Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh bằng a và các góc phẳng đỉnh B đều bằng 600.

    Cặp đường thẳng nào sau đây không vuông góc với nhau?

    Hướng dẫn:

    Hình ảnh minh họa

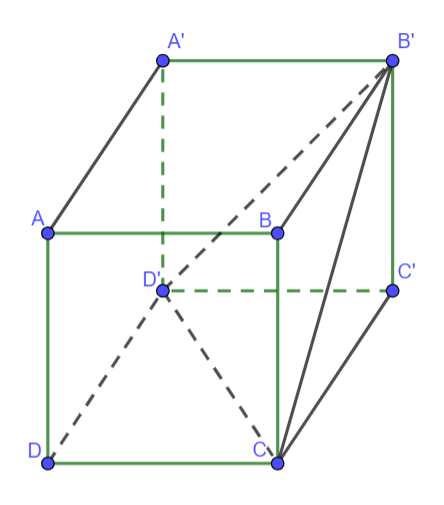
    Cặp đường thẳng nào sau đây không vuông góc với nhau

    Xét tam giác CB'D' có ba cạnh bằng a\sqrt 3 nên tam giác không vuông.

    => B’C và CD’ không vuông góc với nhau.

  • Câu 9: Vận dụng
    Đường thẳng B’C vuông góc với đường thẳng nào

    Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh bằng a và các góc tại đỉnh B đều bằng 600.

    Đường thẳng B’C vuông góc với đường thẳng:

    Hướng dẫn:

    Hình vẽ minh họa:

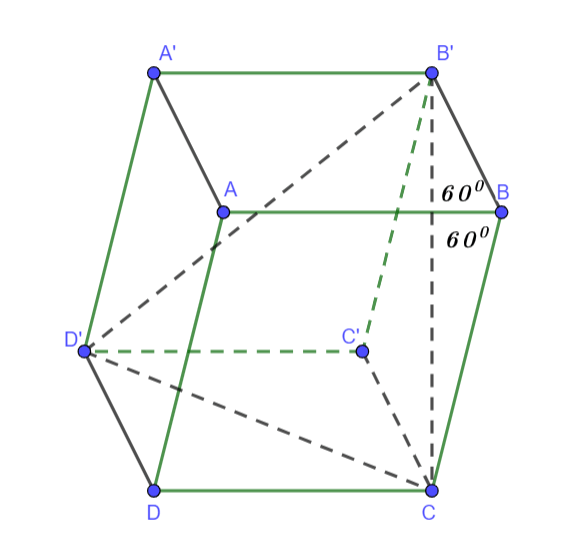
    Đường thẳng B’C vuông góc với đường thẳng nào

    Ta có: 

    \begin{matrix} \overrightarrow {CB'} .\overrightarrow {CD} = \left( {\overrightarrow {CC'} + \overrightarrow {C'B'} } ight).\overrightarrow {CD} \hfill \\ = \overrightarrow {CC'} .\overrightarrow {CD} + \overrightarrow {C'B'} .\overrightarrow {CD} \hfill \\ = CC'.CD.\cos \widehat {C'CD} + C'B'.CD.\cos \widehat {B'C'D'} \hfill \\ = a.a.\cos {60^0} + a.a.\cos \left( {{{180}^0} - \widehat {ABC}} ight) \hfill \\ = \dfrac{{{a^2}}}{2} - \dfrac{{{a^2}}}{2} = 0 \hfill \\ \end{matrix}

  • Câu 10: Vận dụng
    Hoàn thành mệnh đề

    Cho tứ diện ABCD. Nếu AB ⊥CD, AC ⊥ BD và BC ⊥ AD thì:

    Hướng dẫn:

    Ta có:

    \begin{matrix} \overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AC} .\overrightarrow {BD} = \overrightarrow {AD} .\overrightarrow {CB} = 0 \hfill \\ \Rightarrow \overrightarrow {AB} .\left( {\overrightarrow {AD} - \overrightarrow {AC} } ight) = \overrightarrow {AC} \left( {\overrightarrow {AD} - \overrightarrow {AB} } ight) \hfill \\ = \overrightarrow {AD} .\left( {\overrightarrow {AB} - \overrightarrow {AC} } ight) = 0 \hfill \\ \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {AB} .\overrightarrow {AD} \hfill \\ \end{matrix}

  • Câu 11: Vận dụng
    Góc giữa hai vecto

    Cho tứ diện ABCD có AB = AC = AD; \widehat {BAC} = \widehat {BAD} = {60^0}. Gọi M và N là trung điểm của AB và CD. Góc giữa \overrightarrow {AB} và \overrightarrow {CD} bằng:

    Hướng dẫn:

    Hình vẽ minh họa

    Góc giữa hai vecto

    Ta có:

    \begin{matrix} \overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AB} .\left( {\overrightarrow {AD} - \overrightarrow {AC} } ight) \hfill \\ = \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC} \hfill \\ = \left| {\overrightarrow {AB} } ight|.\left| {\overrightarrow {AD} } ight|\cos \left( {\overrightarrow {AB} ;\overrightarrow {AD} } ight) \hfill \\ - \left| {\overrightarrow {AB} } ight|.\left| {\overrightarrow {AC} } ight|.\cos \left( {\overrightarrow {AB} ;\overrightarrow {AC} } ight) \hfill \\ = \left| {\overrightarrow {AB} } ight|.\left| {\overrightarrow {AD} } ight|\cos {60^0} \hfill \\ - \left| {\overrightarrow {AB} } ight|.\left| {\overrightarrow {AC} } ight|.\cos {60^0} \hfill \\ \end{matrix}

    Mà AC = AD

    \overrightarrow {AB} .\overrightarrow {CD} = 0 \Rightarrow \left( {\overrightarrow {AB} ;\overrightarrow {CD} } ight) = {90^0}

  • Câu 12: Vận dụng
    Chọn kết luận sai

    Cho tứ diện ABCD có AB = AC = AD; \widehat {BAC} = \widehat {BAD} = {60^0}. Gọi M và N là trung điểm của AB và CD. Kết luận nào sau đây sai?

    Hướng dẫn:

    Hình vẽ minh họa

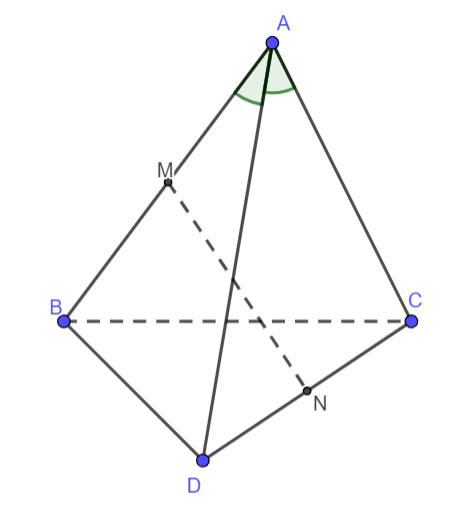
    Chọn kết luận sai

    Xét tam giác ABD có AB = AD và \widehat {BAD} = {60^0}

    => Tam giác ABD là tam giác đều

    => DM = \frac{{AB\sqrt 3 }}{2} (Vì DM là trung tuyến)

    Xét tam giác ABC có AB = AC và \widehat {BAC} = {60^0}

    => Tam giác ABC là tam giác đều

    => CM = \frac{{AB\sqrt 3 }}{2} (Vì CM là trung tuyến)

    => DM = CM nên tam giác MCD cân tại M có MN là trung tuyến (do N là trung điểm của CD)

    Suy ra MN là đường cao của tam giác MCD

    => MN ⊥ CD

    Chứng minh tương tự:

    Vì hai tam giác ACD và BCD bằng nhau (c.c.c) nên hai đường trung tuyến tương ứng AN; BN bằng nhau: AN = BN

    => Tam giác ABN cân tại N có NM là đường trung tuyến nên MN ⊥ AB

    Vậy kết luận "MN không vuông góc với AB và CD" là kết luận sai.

0/12
12 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (42%):
    2/3
  • Thông hiểu (58%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 8 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11

Đăng nhập