Lớp 11 Toán 11 (sách cũ)

Phép đối xứng tâm

1. Phép đối xứng tâm

Định nghĩa

Cho điểm I. Phép biến hình biến điểm I thành chính nó, biến mỗi điểm M khác I thành M' sao cho I là trung điểm của MM' được gọi là phép đối xứng tâm I.

Hình vẽ minh họa

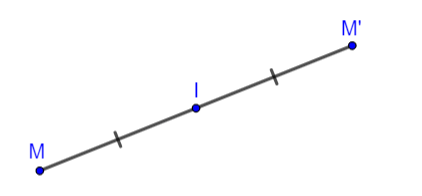
Đối xứng tâm

  • Điểm I được gọi là tâm đối xứng.
  • Phép đối xứng tâm I thường được kí hiệu là Đ_I.
  • Nếu hình H' là ảnh của hình H qua Đ_I thì ta còn nói H đối xứng với H'qua tâm I, hay H và H' đối xứng với nhau qua I.
  • Từ đinh nghĩa suy ra M' = {Đ_I}\left( M \right) \Leftrightarrow \overrightarrow {IM'} = - \overrightarrow {IM}

2. Tính chất của phép đối xứng tâm

Tính chất 1

Nếu Đ_I(M) = M' và Đ_I(N) = N' thì \overrightarrow {M'N'} = - \overrightarrow {MN}, từ đó suy ra M'N' = MN.

Hình vẽ minh họa

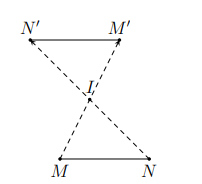
Phép đối xứng tâm

Tính chất 2

Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn cùng bán kính. 

Hình vẽ minh họa

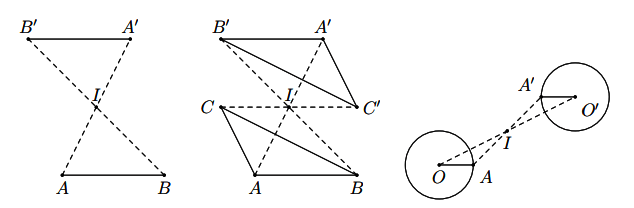
Phép đối xứng tâm

3. Biểu thức tọa độ của phép đối xứng tâm

Với O(0; 0) ta có M'(x';y')=Đ_O[M(x;y)] thì \left\{ {\begin{array}{*{20}{c}} {x' = - x} \\ {y' = - y} \end{array}} \right.

Với I(a;b) ta có M'(x';y')=Đ_I[M(x;y)] thì \left\{ {\begin{array}{*{20}{c}} {x' = 2a- x} \\ {y' = 2b- y} \end{array}} \right.

Ví dụ: Trong mặt phẳng tọa độ Oxycho điểm I(2; −3) và đường thẳng d có phương trình
3x + 2y − 1 = 0. Tìm tọa độ của điểm I' và phương trình của đường thẳng d' lần lượt là ảnh của I và đường thẳng d qua phép đối xứng tâm O.

Hướng dẫn giải

Ta có I’(−2; 3). Từ biểu thức tọa độ của phép đối xứng qua gốc tọa độ ta có \left\{ {\begin{array}{*{20}{l}} {x = - x'} \\ {y = - y'} \end{array}} \right.

Thay biểu thức của x và y vào phương trình của d ta được 3(−x’) + 2(−y’) − 1 = 0, hay 3x’ + 2y’ + 1 = 0

=> Phương trình của d’: 3x + 2y + 1 = 0

4. Tâm đối xứng của một hình

Điểm I được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm I biến hình H thành chính nó. Khi đó ta nói H là hình có tâm đối xứng. 

Câu trắc nghiệm mã số: 9842,9843
  • 1.278 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11