Lớp 11 Toán 11 (sách cũ)

Luyện tập Phép quay

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 15 câu
  • Điểm số bài kiểm tra: 15 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Thông hiểu
    Xác định phép quay

    Cho hình vuông ABCD tâm O. Gọi E, F lần lượt là trung điểm của các cạnh BC và CD.

    Phép biến hình nào sau đây biến \overrightarrow {BE} thành \overrightarrow {CF} là: 

    Hướng dẫn:

    Hình vẽ minh họa

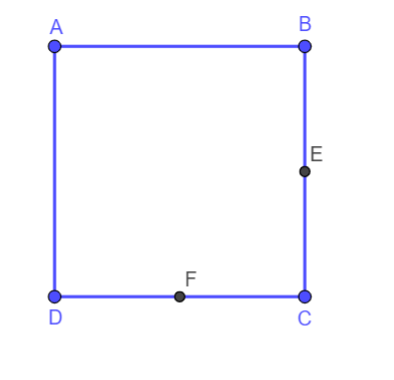
    Xác định phép quay

    Xét từng điểm: Phép quay tâm O góc quay -900 biến B thành C, E thành F.

    Phương án A. Q(A, 450)(B) = B' ≠ C và Q(A, 450)(E) = E' ≠ F(sai cả hai ảnh)

    Phương án C. Q(A, -900)(B) = D và Q(A, 900)(E) = E' ≠ F(sai về chiều góc và ảnh của E)

    Phương án D. Q(O, 900)(B) = A và Q(O, -900)(E) = F

  • Câu 2: Thông hiểu
    Xác định phép quay

    Cho hình vuông ABCD tâm O. Gọi E, F lần lượt là trung điểm của các cạnh BC và CD.

    Phép biến hình nào sau đây biến  \overrightarrow {BE} thành \overrightarrow {DF} là: 

    Hướng dẫn:

     Hình vẽ minh họa

    Xác định phép quay

    Khi luyện tập ta kiểm tra cả bốn phương án và trong mỗi phương án kiểm tra cả hai điểm B, D. còn trong khi kiểm tra, thi cử khi thấy ảnh của một điểm sai thì loại phương án đó; thấy ảnh của cả hai điểm đều đúng thì chọn phương án đó mà không cần kiểm tra các phương án còn lại. 

  • Câu 3: Nhận biết
    Tìm ảnh của điểm M

    Trong mặt phẳng Oxy, ảnh của điểm M (-6; 1) qua phép quay Q(O; 90^{\circ}) là:

    Hướng dẫn:

    Phép quay tâm O góc quay 900 biến điểm M(x; y) thành M’(x’; y’) với biểu thức tọa độ là:

    \left\{ {\begin{array}{*{20}{l}} {x\prime = - y} \\ {y\prime = x} \end{array}} ight.

    Với M(-6; 1) suy ra M’ có tọa độ là:

    \left\{ {\begin{array}{*{20}{l}} {x\prime = - y = - 1} \\ {y\prime = x = - 6} \end{array}} ight.

    => M'(-1; -6).

  • Câu 4: Thông hiểu
    Tìm tọa độ điểm M

    Trong mặt phẳng Oxy qua phép quay Q(O;90^0) thì M'(2; -3) là ảnh của điểm.

    Hướng dẫn:

    Áp dụng công thức tọạ độ của phép quay {Q_{\left( {O;\alpha } ight)}}:M\left( {x;y} ight) \to M'\left( {x';y'} ight) thì biểu thức tọa độ là: \left\{ {\begin{array}{*{20}{c}} {x' = x\cos \alpha - y\sin \alpha } \\ {y' = x\sin \alpha + y\cos \alpha } \end{array}} ight.

    Áp dụng bài toán ta có:

    \begin{matrix} \left\{ {\begin{array}{*{20}{c}} {2 = x\cos {{90}^0} - y\sin {{90}^0}} \\ { - 3 = x\sin {{90}^0} + y\cos {{90}^0}} \end{array}} ight. \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x = - 3} \\ {y = - 2} \end{array}} ight. \Leftrightarrow M\left( {3; - 2} ight) \hfill \\ \end{matrix}

  • Câu 5: Thông hiểu
    Tìm ảnh của điểm M qua phép quay tâm O

    Trong mặt phẳng Oxy cho điểm M(1; 1). Điểm nào sau đây là ảnh của M qua phép quay tâm O, góc quay 45^{\circ}.

    Hướng dẫn:

    Gọi điểm M′(x′; y′) là ảnh của điểm M(1; 1) qua phép quay tâm O góc 450 nên ta có:

    \begin{matrix} \left\{ {\begin{array}{*{20}{c}} {x' = \cos {{45}^0} - \sin {{45}^0}} \\ {y' = \sin {{45}^0} + \cos {{45}^0}} \end{array}} ight. \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x' = 0} \\ {y' = \sqrt 2 } \end{array}} ight. \Leftrightarrow M'\left( {0;\sqrt 2 } ight) \hfill \\ \end{matrix}

  • Câu 6: Nhận biết
    Chọn đáp án đúng

    Có bao nhiêu điểm biến thành chính nó qua phép quay tâm O góc \alpha với \alpha eq k2\pi (k là một số nguyên)?

    Hướng dẫn:

    Có 1 điểm biến thành chính nó qua phép quay tâm O góc \alpha với \alpha eq k2\pi (k là một số nguyên).

  • Câu 7: Thông hiểu
    Xác định góc quay

    Cho tam giác đều tâm O. Với giá trị nào dưới đây của \varphi thì phép quay Q_{(O,\varphi)} biến tam giác đều thành chính nó?

    Hướng dẫn:

     Các góc quay để biến tam giác đều thành chính nó là: 0;\frac{{2\pi }}{3};\frac{{4\pi }}{3};2\pi

  • Câu 8: Thông hiểu
    Chọn mệnh đề sai

     Cho hình lục giác ABCDEF, tâm O. Mệnh đề nào sau đây sai?

    Hướng dẫn:

    Hình vẽ minh họa:

    Chọn mệnh đề sai

    Xét phép quay tâm O góc quay −600:

    \begin{matrix} {Q_O}\left( A ight) = B; \hfill \\ {Q_O}\left( F ight) = A; \hfill \\ {Q_O}\left( D ight) = E \hfill \\ \end{matrix}

    Do đó, phép quay tâm O góc quay - 600 biến tam giác AFD thành tam giác BAE.

  • Câu 9: Thông hiểu
    Tam giác BFG là tam giác gì

    Cho ba điểm thẳng hàng A, B, C. Dựng các tam giác đều ABD, BCE về cùng phía đối với đường thẳng AC. Gọi F, G lần lượt là trung điểm của các cạnh AE và DC. Tam giác BFG là:

    Hướng dẫn:

    Hình vẽ minh họa

    Tam giác BFG là tam giác gì

    Xét phép quay tâm B góc quay -600 biến A thành D, biến E thành C

    => Phép quay này biến đoạn thẳng AE thành đoạn thẳng DC.

    Suy ra nó biến trung điểm F của AE thành trung điểm G của DC.

    Suy ra nó biến đoạn thẳng BF thành đoạn thẳng BG do đó BF = BG và góc FBG bằng 600.

    Vậy tam giác BFG là tam giác đều.

  • Câu 10: Thông hiểu
    Tìm phép biến hình biến AB thành BC

    Cho hình thoi ABCD có góc A bằng 60^0.Phép biến hình nào sau đây biến AB thành BC?

    Hướng dẫn:

    ĐO(AB) = CD.

    T_{2\vec{OC}} (AB)=CB' với ACB'B là hình bình hành.

    Q(B,1200)(AB) = A'B với A' là điểm đối xứng của D và B.

    Góc quay là -1200 (thuận chiều kim đồng hồ) thì A biến thành C.

  • Câu 11: Thông hiểu
    Chọn đáp án sai

    Cho hình thoi ABCD có góc A bằng 60^0. Phép biến hình nào sau đây không biến A thành C?

    Hướng dẫn:

    Phép biến hình không biến A thành C là Q_{(B; 120^{\circ})}

  • Câu 12: Thông hiểu
    Tìm tọa độ điểm K

    Trong mặt phẳng Oxy phép quay tâm K, góc 60^0 biến M(1; 1) thành M’(-1; 1). Tọa độ điểm K là:

    Hướng dẫn:

    Tam giác đều KMM’ có cạnh MM’ = 2 nên đường cao bằng \sqrt 3

    =>OK = \sqrt 3 - 1 \Rightarrow K\left( {0;1 - \sqrt 3 } ight)

    Nhận xét: Phép quay có góc quay bằng ±600 thì tam giác tạo bởi tâm quay, điểm M và ảnh M’ của nó luôn tạo thành một tam giác đều.

  • Câu 13: Thông hiểu
    Viết phương trình đường thẳng d'

    Trong mặt phẳng Oxy phép quay Q(O; 90^0) biến đường thẳng d có phương trình x - 2y = 0 thành đường thẳng d’ có phương trình:

    Hướng dẫn:

    Lấy M(2; 1) thuộc d, phép quay Q(O, 900) biến M(2; 1) thành M’(-1; 2). Tâm quay O(0; 0) thuộc d.

    => d' đi qua O và M’ có phương trình 2x + y = 0. 

  • Câu 14: Thông hiểu
    Viết phương trình d'

    Trong mặt phẳng Oxy phép quay Q (O; 90^{\circ}) biến đường thẳng d có phương trình: 2x - y + 1 = 0 thành đường thẳng d’ có phương trình.

    Hướng dẫn:

    Lấy A(0; 1) và B(-1/2;0) thuộc d, phép quay Q(O; 900) biến A thành A’(-1; 0), biến B thành B’(0; -1/2)

    Ta viết phương trình đường thẳng A'B':

    Đi qua A' (-1; 0) và có vecto chỉ phương \overrightarrow {AB} \left( {1; - \frac{1}{2}} ight) nên có vecto pháp tuyến (1; 2 )

    Phương trình d’ qua A’, B’ là

    1. (x + 1) + 2.( y - 0) = 0

    Hay x + 2y + 1 = 0.

  • Câu 15: Thông hiểu
    Tìm ảnh của đường tròn (C)

    Trong mặt phẳng Oxy cho đường tròn (C) có phương trình (x - 3)^{2} + y^{2} = 4 . Phép quay tâm O(0; 0) góc quay 90^0 biến (C) thành (C’) có phương trình:

    Hướng dẫn:

    Phép quay tâm O(0; 0) góc quay 900 biến tâm I(3; 0) của (C) thành tâm I’(0; 3) của (C’), bán kính không thay đổi. phương trình (C’) là:

    \begin{matrix} {x^2} + {\left( {y - 3} ight)^2} = 4 \hfill \\ \Rightarrow {x^2} + {y^2} - 6y + 5 = 0 \hfill \\ \end{matrix}

0/15
15 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (13%):
    2/3
  • Thông hiểu (87%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 6 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11

Đăng nhập