Lớp 11 Toán 11 (sách cũ)

Luyện tập Phép tịnh tiến

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 15 câu
  • Điểm số bài kiểm tra: 15 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Thông hiểu
    Viết phương trình đường thẳng d'

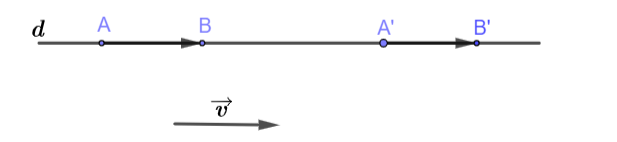
    Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto \overrightarrow v \left( {3;1} ight) biến đường thẳng d: 12x - 36y + 101 = 0 thành đường thẳng d’ có phương trình:

    Hướng dẫn:

    Đường thẳng d có vecto pháp tuyến là: \overrightarrow n \left( {12; - 36} ight) = 12\left( {1; - 3} ight)

    => Vecto chỉ phương của đường thẳng d là \overrightarrow u = \left( {3;1} ight)

    Vì vecto chỉ phương của d cùng phương với vecto \overrightarrow v nên phép tịnh tiến theo vecto \overrightarrow v \left( {3;1} ight) biến đường thẳng d thành chính nó.

    => d':12x – 36y + 101 = 0

  • Câu 2: Thông hiểu
    Viết phương trình (P')

    Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto \overrightarrow v \left( { - 2; - 1} ight) biến thành parabol (P): y=x^2  thành parabol (P’) có phương trình:

    Hướng dẫn:

    Qua phép tịnh tiến theo \overrightarrow v biến (P) thành (P'). Lấy M(x; y) thuộc (P); gọi M’(x’; y’) là ảnh của M qua phép tịnh tiến theo vecto \overrightarrow v \left( { - 2; - 1} ight) thì điểm M' thuộc (P').

    Áp dụng biểu thức tọa độ của phép tịnh tiến ta có:

    \left\{ {\begin{array}{*{20}{c}} {x' - x = - 2} \\ {y' - y = - 1} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x = x' + 2} \\ {y = y' + 1} \end{array}} ight.

    Thay vào phương trình (P) ta được:

    \begin{matrix} y' + 1 = {\left( {x' + 1} ight)^2} \hfill \\ \Rightarrow y' = x{'^2} + 4x' + 3 \hfill \\ \end{matrix}

    Hay y = {x^2} + 4x + 3

  • Câu 3: Vận dụng
    Viết phương trình đường tròn (C')

    Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto \overrightarrow v \left( { - 3; - 2} ight) biến đường tròn có phương trình (C): {x^2} + {(y - 1)^2} = 1 thành đường tròn (C’) có phương trình:

    Hướng dẫn:

     Đường tròn (C) có tâm I(0; 1), bán kính R = 1

    Gọi I′(x; y) là ảnh của I(0; 1) qua phép tịnh tiến vectơ \overrightarrow v \left( { - 3; - 2} ight)

    Ta có: 

    \begin{matrix} \overrightarrow {II'} = \overrightarrow v \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {x - 0 = - 3} \\ {y - 1 = - 2} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {x = - 3} \\ {y = - 1} \end{array}} ight. \hfill \\ \Rightarrow I\prime \left( { - 3; - 1} ight) \hfill \\ \end{matrix}

    Vì phép tịnh tiến bảo toàn khoảng cách nên R′ = R = 1

    Vậy ảnh của đường tròn (C) qua phép {T_{\overrightarrow v }} là đường tròn (C′) có tâm I′(−3;−1), bán kính T nên có phương trình (C′):(x+3)^2+(y+1)^2=1.

  • Câu 4: Nhận biết
    Xác định số phép tịnh tiến biến một đường tròn thành chính nó

    Có bao nhiêu phép tịnh tiến biến một đường tròn cho trước thành chính nó?

    Hướng dẫn:

    Có đúng một phép tịnh tiến biến một đường tròn cho trước thành chính nó. Tịnh tiến theo vectơ – không.

  • Câu 5: Nhận biết
    Có bao nhiêu phép tịnh tiến biến một hình vuông thành chính nó

    Có bao nhiêu phép tịnh tiến biến một hình vuông cho trước thành chính nó?

    Hướng dẫn:

    Có đúng một phép tịnh tiến biến một hình vuông cho trước thành chính nó.

    Tịnh tiến theo vectơ–không.

  • Câu 6: Nhận biết
    Có bao nhiêu phép tịnh tiến biến một đường thẳng thành chính nó

    Có bao nhiêu phép tịnh tiến biến một đường thẳng cho trước thành chính nó?

    Hướng dẫn:

    Mọi phép tịnh tiến theo vectơ có giá song song hoặc trùng với đường thẳng d đều biến d thành chính nó.

    Hình vẽ minh họa

    Có bao nhiêu phép tịnh tiến biến một đường thẳng thành chính nó

    Vậy có vô số phép tịnh tiến như trên.

  • Câu 7: Thông hiểu
    Có bao nhiêu phép tịnh tiến biến d thành d'

    Cho hai đường thẳng d và d' song song với nhau. Có bao nhiêu phép tịnh tiến biến d thành d'?

    Hướng dẫn:

    Trên hai đường thẳng d, d' đã cho lần lượt lấy hai điểm A, A' bất kì.

    Khi đó d' là ảnh của d qua phép tịnh tiến vectơ \overrightarrow {AA'}

    Vậy có vô số phép tịnh tiến biến d thành d' thỏa mãn d song song d'.

    Hình vẽ minh họa

    Có bao nhiêu phép tịnh tiến biến d thành d'

  • Câu 8: Thông hiểu
    Có bao nhiêu phép tịnh tiến biến a thành a' và b thành b'

    Cho bốn đường thẳng a, b, a', b' trong đó a // a', b // b' và a cắt b. Có bao nhiêu phép tịnh tiến biến a thành a' và b thành b'?

    Hướng dẫn:

    Có suy nhất một phép tịnh tiến biến a thành a' và b thành b'

  • Câu 9: Thông hiểu
    Chọn mệnh đề đúng

    Tìm mệnh đề đúng trong các mệnh đề sau:

    Hướng dẫn:

    Phương án: "Phép tịnh tiến theo vecto \vec{v} biến M thành M’ thì \overrightarrow v = \overrightarrow {M'M}" sai vì \overrightarrow v = \overrightarrow {MM'}.

    Phương án: "Phép tịnh tiến theo vecto \vec{v} biến M thành M’ và N thành N’ thì tứ giác MNM’N’ là hình bình hành." sai vì tứ giác MNN'M’ là hình bình hành.

    Phương án: "Phép tịnh tiến theo vecto \vec{v} biến đường tròn (O; R) thành đường tròn (O; R)" sai vì phép tịnh tiến theo vecto \vec{v} chỉ biến đường tròn (O; R) thành đường tròn (O; R) khi vecto tịnh tiến bằng vecto không. 

  • Câu 10: Thông hiểu
    Tìm mệnh đề sai

    Cho tam giác ABC có trọng tâm G. Gọi D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB. Mệnh đề nào sau đây là sai?

    Hướng dẫn:

    Ta có: D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB

    Do đó: DE, EF, FD là các đường trung bình của tam giác ABC

    Suy ra: \left\{ {\begin{array}{*{20}{l}} {FE// = \dfrac{1}{2}BC} \\ {DE// = \dfrac{1}{2}AB} \\ {DF// = \dfrac{1}{2}AC} \end{array}} ight.

    Do đó ta có các phép tịnh tiến như sau: T_{\frac{1}{2}\vec{BC}}(F) =E, T_{\vec{DE}}(B)=F

    Lại có G là trọng tâm tam giác ABC nên ta có DG = \frac{1}{2}GA

    \Rightarrow {T_{\frac{1}{2}\overrightarrow {GA} }}(D)= G;{T_{2\overrightarrow {DG} }}(G) = A

    Vậy đáp án T_{\frac{1}{2}\vec{BC}}(F) =E, T_{\vec{DE}}(B)=F, T_{\frac{1}{2}\vec{GA}}(D) = G là các đáp án đúng.

  • Câu 11: Nhận biết
    Tìm tọa độ M'

    Trong mặt phẳng tọa độ, phép tịnh tiến theo \vec{v}(1;2) biến điểm M (-1; 4) thành điểm M’ có tọa độ là:

    Hướng dẫn:

    Gọi tọa độ điểm M'(x'; y')

    Thay tọa độ M và vecto \overrightarrow v vào công thức:

    \begin{matrix} \left\{ {\begin{array}{*{20}{l}} {x\prime = x + 1} \\ {y\prime = y + 2} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {x\prime = - 1 + 1} \\ {y\prime = 4 + 2} \end{array}} ight. \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {x\prime = 0} \\ {y\prime = 6} \end{array}} ight. \Rightarrow M'\left( {0;6} ight) \hfill \\ \end{matrix}

  • Câu 12: Thông hiểu
    Tính tọa độ vecto

    Trong mặt phẳng tọa độ cho điểm M(-10; 1) và điểm M’(3; 8). Phép tịnh tiến theo \vec{v} biến M thành M’ thì tọa độ vecto \vec{v} là:

    Hướng dẫn:

    Gọi tọa độ vecto cần tìm là: \overrightarrow v = \left( {a;b} ight)

    Thay vào công thức như sau:

    \begin{matrix} \left\{ {\begin{array}{*{20}{l}} {x\prime = x + a} \\ {y\prime = y + b} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} { - 10 = 3 + a} \\ {1 = 8 + b} \end{array}} ight. \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {a = - 13} \\ {b = - 7} \end{array}} ight. \Rightarrow \overrightarrow v = \left( { - 13; - 7} ight) = \left( {13;7} ight) \hfill \\ \end{matrix}

  • Câu 13: Thông hiểu
    Tìm tọa độ ảnh A' của A

    Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto \vec{v}(0; 0) biến điểm A(0; 2) thành điểm A’ có tọa độ:

    Hướng dẫn:

    Phép tịnh tiến theo vecto không biến mỗi điểm thành chính nó.

    => A’(0; 2)

  • Câu 14: Vận dụng
    Tính độ dài A'B'

    Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto \vec{v}(1; 1) biến điểm A(0; 2) thành A’ và biến điểm B(-2; 1) thành B’ khi đó:

    Hướng dẫn:

    Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.

    Phép tịnh tiến theo vecto  \vec{v}(1; 1)  biến A(0; 2) thành A’(1; 3) và biến B(-2; 1) thành B’(-1; 2)

    => A'B' = AB = \sqrt {{{\left( { - 2 - 0} ight)}^2} + {{\left( {1 - 2} ight)}^2}} = \sqrt 5

  • Câu 15: Thông hiểu
    Viết phương trình đường thẳng d'

    Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto \vec{v}(1; 0) biến đường thẳng d: x - 1 = 0 thành đường thẳng d’ có phương trình:

    Hướng dẫn:

    Lấy M(x; y) thuộc d. Gọi M’(x’; y’) là ảnh của M qua phép tịnh tiến theo vecto \vec{v}(1; 0) thì

    \left\{ {\begin{array}{*{20}{l}} {x\prime - x = 1} \\ {y\prime - y = 0} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {x = x' - 1} \\ {y = y'} \end{array}} ight.

    Thay vào phương trình d ta được x’ – 2 = 0, hay phương trình d’ là x – 2 = 0.

0/15
15 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (27%):
    2/3
  • Thông hiểu (60%):
    2/3
  • Vận dụng (13%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 5 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11

Đăng nhập