Lớp 11 Toán 11 (sách cũ)

Phép thử và biến cố

1. Phép thử, không gian mẫu

Một trong những khái niệm cơ bản của lí thuyết xác suất là phép thử. Một thí nghiệm, một phép đo hay một sự quan sát hiện tượng nào đó,... được gọi là phép thử.

Phép thử ngẫu nhiên

Phép thử ngẫu nhiên là phép thử mà ta không đoán trước được kết quả của nó, mặc dù đã biết tập hợp tất cả các kết quả có thể có của phép thử đó.

Để đơn giản ta gọi tắt phép thử ngẫu nhiên là phép thử và trong chương trình toán phổ thông ta
chỉ xét phép thử có hữu hạn kết quả.

Không gian mẫu

Tập hợp các kết quả có thể xảy ra của một phép thử được gọi là không gian mẫu của phép thử và kí hiệu là Ω (đọc là ô-mê-ga). 

Ví dụ: Gieo một con xúc xắc hai lần liên tiếp. Hãy mô tả không gian mẫu của phép thử.

Hướng dẫn giải

Không gian mẫu của phép thử \Omega = \;\left\{ {\left( {i;j} \right)|i = \overline {1,6} ,{\text{ }}j = \overline {1,6} } \right\}

Câu trắc nghiệm mã số: 22027,22028

2. Biến cố

Định nghĩa

  • Biến cố là một tập con của không gian mẫu.
  • Mỗi biến cố liên quan đến một phép thử được mô tả bởi một tập con của không gian mẫu, tức là một tập hợp bao gồm các kết quả nào đó của phép thử.

Chú ý:

  • Biến cố có thể được cho dưới dạng một mệnh đề xác định tập hợp. Kí hiệu các biến cố bằng các chữ in hoa A, B, C, ...
  • Khi nói cho các biến cố A, B, ... mà không nói gì thêm thì ta hiểu chúng cùng liên quan đến một phép thử.

Định nghĩa

  • Tập \emptyset được gọi là biến cố không thể (gọi tắt là biến cố không).
  • Tập Ω được gọi là biến cố chắc chắn.

Biến cố A xảy ra trong một phép thử nào đó khi và chỉ khi kết quả của phép thử đó là một phần tử của A (hay thuận lợi cho A.

Ví dụ: Gieo một con súc sắc hai lần, biến cố A: "Tổng số chấm trên mặt xuất hiện của hai
lần gieo là số chẵn", và biến cố B là biến cố đối của biến cố A. Xác định biến cố B và liệt kê các kết quả thuận lợi cho B.

Hướng dẫn giải

B: "Tổng số chấm trên mặt xuất hiện của hai lần gieo là số lẻ".

\begin{matrix} B = \{ \left( {1,2} \right);\left( {1,4} \right);\left( {1,6} \right);\left( {2,1} \right);\left( {2,3} \right); \hfill \\ \left( {2,5} \right);\left( {3,2} \right);\left( {3,4} \right);\left( {3,6} \right);\left( {4,1} \right);\left( {4,3} \right); \hfill \\ \left( {4,5} \right);\left( {5,2} \right);\left( {5,4} \right);\left( {5,6} \right);\left( {6,1} \right);\left( {6,3} \right);\left( {6,5} \right)\} \hfill \\ \end{matrix}

3. Phép toán trên các biến cố

Giả sử A và B là hai biến cố liên quan đến một phép thử.

Định nghĩa

Tập Ω \setminus A được gọi là biến cố đối của biến cố A, kí hiệu \overline A

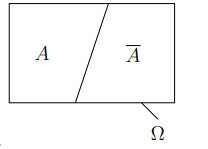
Phép thử và biến cố

Chú ý: \overline A xảy ra khi và chỉ khi A không xảy ra.

Định nghĩa

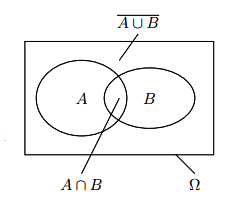
  • Tập A ∪ B được gọi là hợp của biến cố A và B.
  • Tập A ∩ B được gọi là giao của biến cố A và B.
  • Nếu A ∩ B = ∅ thì ta nói A và B xung khắc.

Chú ý: 

  • A ∪ B xảy ra khi và chỉ khi A xảy ra hoặc B xảy ra.
  • A ∩ B xảy ra khi và chỉ khi A và B đồng thời xảy ra.
  • Biến cố 
  • A ∩ Bcòn được viết là A.B.
  • A và B xung khắc khi và chỉ khi chúng không khi nào cùng xảy ra.

Kí hiệu

Ngôn ngữ biến cố

A ⊂ Ω

A là biến cố

A = ∅

A là biến cố không

A = Ω

A là biến cố chắc chắn

C = A ∪ B

C là biến cố: "A hoặc B"

C = A ∩ B

C là biến cố: "A và B"

A ∩ B = ∅

A và B xung khắc

B = A

A và B đối nhau

Ví dụ: Lớp 11A có 35 học sinh. Trong đó có 10 bạn là học sinh giỏi môn Văn, 7 bạn là học sinh giỏi môn Toán, và 2 bạn là học sinh giỏi cả hai môn. Chọn một học sinh đi thi giao thông học đường.

Xét biến cố:

A: "Bạn được chọn là học sinh giỏi Văn";

B: "Bạn được chọn là học sinh giỏi Toán";

C: "Bạn được chọn là học sinh vừa giỏi Văn vừa giỏi Toán".

Xét tính đúng sai của các mệnh đề sau.

a) A ∪ B ∪ C = Ω

b) A và B là hai biến cố xung khắc nhau;

c) A và B là hai biến cố đối nhau;

d) A \setminus B là biến cố đối của biến cố B \setminus A;

e) \overline A \cap \overline B và A ∪ B là hai biến cố đối nhau;

f) A \cap \overline B và \overline A \cap \overline B là hai biến cố xung khắc.

Hướng dẫn giải

Phép thử và biến cố

a) Mệnh đề sai A \cup B \cup C = \Omega \backslash \overline {A \cup B}

b) Mệnh đề sai vì A \cap B = C \ne \emptyset

c) Mệnh đề sai vì A \cap B = C \ne \emptyset

d) Mệnh đề sai. \left( {A\backslash B} \right) \cap \left( {A\backslash B} \right) = \emptyset, nhưng \left( {A\backslash B} \right) \cup \left( {A\backslash B} \right) \ne \Omega.

Đây là hai biến cố xung khắc nhưng không phải hai biến cố đối nhau.

e) Mệnh đề đúng vì \overline A \cap \overline B = \overline {A \cup B}

f) Mệnh đề đúng. Vì \forall x \in A \cap \overline B \Leftrightarrow \left\{ \begin{gathered} x \in A \hfill \\ x \in B \hfill \\ \end{gathered} \right. \Rightarrow \left[ \begin{gathered} x \notin \overline A {\text{ }} \hfill \\ x \notin B \hfill \\ \end{gathered} \right.

Tương tự với tập \overline A \cap B.

=> Hai tập là xung khắc nhau

Câu trắc nghiệm mã số: 9527,9519,9518
  • 1.575 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11