Luyện tập Phép đối xứng tâm

 Mệnh đề đúng là: "Hình bình hành có tâm đối xứng."

Hình không có tâm đối xứng là tam giác đều.

 Hình gồm một đường tròn và một tam giác đều nội tiếp không có tâm đối xứng.

Đường elip có tâm đối xứng là trung điểm của đoạn nối hai tiêu điểm.

Đường tròn có tâm đối xứng là tâm đường tròn.

Đường parabol không có tâm đối xứng.

Hình vuông có tâm đối xứng là giao điểm hai đường chéo.

Hình bình hành có tâm đối xứng.

Hình chữ nhật vừa có tâm đối xứng vừa có trục đối xứng.

Hình tam giác cân và hình tam giác đều chỉ có trục đối xứng. 

Hình chữ nhật có 1 tâm đối xứng là giao điểm của 2 đường chéo

=> Có duy nhất một phép đối xứng tâm biến hình chữ nhật thành chính nó.

Phép đối xứng tâm biến điểm M(x; y) thành M'(x'; y') thì:

Phép đối xứng tâm I biến điểm M(x; y) thành điểm M'(x'; y') nên I là trung điểm của đoạn thẳng MM' nên ta có:

Qua phép đối xứng tâm I biến M thành M' nên I là trung điểm của MM' khi đó ta có:

Thay tọa độ điểm I vào phương trình đường thẳng d ta được:

6. 2 + 5. (-1) - 7 = 0

=> Điểm I nằm trên đường thẳng d

Vì tâm đối xứng I thuộc d thì phép đối xứng tâm I biến d thành chính nó.

Hai đường thẳng d và d’ song song.

Vì điểm A(1; 2) thuộc d và điểm B(-4; 0) thuộc d’ nên =>  và  bị loại

Xét điểm . Tính khoảng cách từ C tới hai đường thẳng d, d’:

 => d(C; d) = d(C; d') => C là tâm đối xứng của hình 

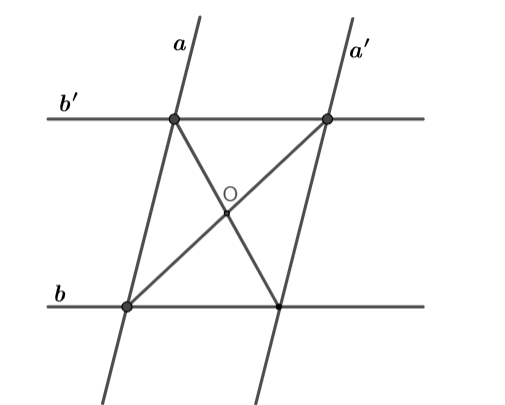
Đó là phép đối xứng qua tâm hình bình hành tạo thành bởi bốn đường thẳng đã cho.

Hình bát giác đều vừa có tâm đối xứng, vừa có trục đối xứng.

Hình tam giác đều có trục đối xứng nhưng không có tâm đối xứng.