Lớp 11 Toán 11

Nhị thức Newton

I. Nhị thức Newton

Định lí

Với \forall n\in {{\mathbb{N}}^{*}} với cặp số \left( a,b \right) ta có:

{{\left( a+b \right)}^{n}}=\sum\limits_{k=0}^{n}{C_{n}^{k}{{a}^{n-k}}}{{b}^{k}}=C_{n}^{0}{{a}^{n}}+C_{n}^{1}{{a}^{n-1}}b+C_{n}^{2}{{a}^{n-2}}{{b}^{2}}+...+C_{n}^{n-1}{{a}^{1}}{{b}^{n-1}}+C_{n}^{n}{{b}^{n}}

Hệ quả

{{\left( 1+x \right)}^{n}}=C_{n}^{0}+xC_{n}^{1}+{{x}^{2}}C_{n}^{2}+...+{{x}^{n}}C_{n}^{n}

  • Với a=b=1 ta có {{2}^{n}}=C_{n}^{0}+C_{n}^{1}+C_{n}^{2}+...+C_{n}^{n}
  • Với a=1;b=-1C_{n}^{0}-C_{n}^{1}+C_{n}^{2}-C_{n}^{3}+...+{{\left( -1 \right)}^{n}}C_{n}^{n}=0

Chú ý: Trong khai triển Newton {{\left( a+b \right)}^{n}} có tính chất sau:

  • Gồm n + 1 phần tử.
  • Số mũ của a giảm từ n đến 0 và số mũ của b tăng từ 0 đến n.
  • Tổng số mũ của a và b trong mỗi số hạng bằng n .
  • Các hệ số có tính đối xứng C_{n}^{k}=C_{n}^{n-k},\left( 0\le k\le n \right).
  • Số hạng tổng quát: {{T}_{k+1}}=C_{n}^{k}{{a}^{b-k}}{{b}^{k}}
  • Số hạng thứ nhất {{T}_{1}}={{T}_{0+1}}=C_{n}^{0}{{a}^{n}}
  • Số hạng thứ k: {{T}_{k}}={{T}_{k-1+1}}=C_{n}^{k-1}{{a}^{n-k+1}}{{b}^{k-1}}

Ví dụ 1: Viết khai triển theo công thức nhị thức Newton:

a, {{\left( a+2b \right)}^{5}} b, {{\left( a-\sqrt{2} \right)}^{6}}

Hướng dẫn giải

a. Khai triển Newton của {{\left( a+2b \right)}^{5}}

{{\left( a+2b \right)}^{5}}=\sum\limits_{k=0}^{5}{C_{5}^{k}{{a}^{5-k}}{{\left( 2b \right)}^{k}}}=\sum\limits_{k=0}^{5}{C_{5}^{k}{{a}^{5-k}}{{.2}^{k}}.{{b}^{k}}}

{{\left( a+2b \right)}^{5}}=C_{5}^{0}{{a}^{5}}+C_{5}^{1}{{a}^{4}}2b+...+C_{5}^{5}32{{b}^{5}}

b. Khai triển Newton của {{\left( a-\sqrt{2} \right)}^{6}}

{{\left( a-\sqrt{2} \right)}^{6}}=\sum\limits_{k=0}^{6}{C_{6}^{k}{{a}^{6-k}}{{\left( \sqrt{2} \right)}^{k}}}

{{\left( a-\sqrt{2} \right)}^{6}}=C_{6}^{0}{{a}^{6}}+C_{6}^{1}{{a}^{5}}.\sqrt{2}+C_{6}^{2}{{a}^{4}}.2+...+C_{6}^{6}.{{\left( \sqrt{2} \right)}^{6}}

Ví dụ 2: Tìm hệ số của {{x}^{7}} trong khai triển biểu thức {{\left( 1-2x \right)}^{10}}

Hướng dẫn giải

Ta có: f\left( x \right)={{\left( 1-2x \right)}^{10}}=\sum\limits_{k=0}^{10}{C_{10}^{k}{{.1}^{10-k}}{{\left( -2x \right)}^{k}}=}\sum\limits_{k=0}^{10}{C_{n}^{k}.{{\left( -2 \right)}^{k}}.{{x}^{k}}}

Số hạng chứa {{x}^{7}} trong khai triển ứng với k = 7. Khi đó hệ số của số hạng chứa {{x}^{7}}:

 C_{10}^{7}.{{\left( -2 \right)}^{7}}=-15360

Ví dụ 3: Tìm hệ số không chứa x trong khai triển sau: {{\left( {{x}^{3}}-\frac{2}{x} \right)}^{n}}biết rằng:

C_{n}^{n-1}+C_{n}^{n-2}=78,x>0

Hướng dẫn giải

Ta có: C_{n}^{n-1}+C_{n}^{n-2}=78,n>2

\Leftrightarrow \frac{n!}{\left( n-1 \right)!(n-n+1)!}+\frac{n!}{\left( n-2 \right)!\left( n-2+2 \right)!}=78

\Leftrightarrow \frac{n!}{\left( n-1 \right)!(1)!}+\frac{n!}{\left( n-2 \right)!\left( 2 \right)!}=78

\Leftrightarrow n+\frac{n\left( n-1 \right)}{2}=78\Leftrightarrow {{n}^{2}}+n-156=0\Leftrightarrow \left[ \begin{matrix} n=12\left( TM \right) \\ n=-13\left( L \right) \\ \end{matrix} \right.

Do đó biểu thức khai triển là {{\left( {{x}^{3}}-\frac{2}{x} \right)}^{12}}=\sum\limits_{k=0}^{12}{C_{12}^{k}{{\left( {{x}^{3}} \right)}^{12-k}}{{\left( -\frac{2}{x} \right)}^{k}}}

=\sum\limits_{k=0}^{12}{C_{12}^{k}.{{x}^{36-3k}}.{{\left( \frac{1}{x} \right)}^{k}}.{{\left( -2 \right)}^{k}}}=\sum\limits_{k=0}^{12}{C_{12}^{k}.{{x}^{36-4k}}.{{\left( -2 \right)}^{k}}}

Số hạng không chứa x ứng với k: 36-4k=0\Leftrightarrow k=9

Số hạng không chưa x là: C_{12}^{9}.{{\left( -2 \right)}^{9}}=-112640

Ví dụ 4: Xét khai triển: {{\left( 2x+\frac{1}{x} \right)}^{20}}

a. Viết số hạng thứ k + 1 trong khai triển.

b. Số hạng nào trong khai triển không chứa x.

c. Xác định hệ số của {{x}^{4}} trong khai triển.

Hướng dẫn giải

{{\left( 2x+\frac{1}{x} \right)}^{20}}=\sum\limits_{k=0}^{20}{C_{20}^{k}{{\left( 2x \right)}^{20-k}}{{\left( \frac{1}{x} \right)}^{k}}=}\sum\limits_{k=0}^{20}{C_{20}^{k}{{2}^{20-k}}{{x}^{20-2k}}}

Số hạng không chứa x trong khai triển ứng với k là: 20-2k=0\Leftrightarrow k=10

Số hạng không chứa x trong khai triển là: C_{20}^{10}{{.2}^{10}}

Số hạng chứa {{x}^{4}} trong khai triển ứng với k là: 20-2k=4\Leftrightarrow k=8

Vậy số hạng chứa {{x}^{4}} trong khai triển có hệ số là: C_{20}^{8}{{.2}^{12}}

II. Tam giác Pascal

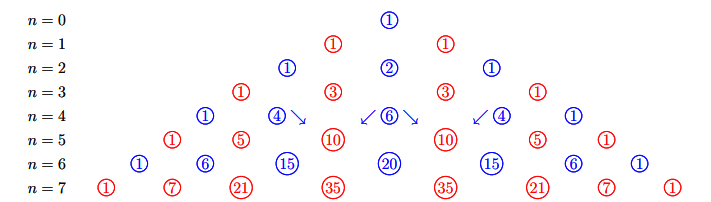
Trong công thức nhị thức Newton, cho n=0,1,... và sắp xếp các hệ số thành dòng, ta nhận được tam giác sau đây, gọi là tam giác Pascal.

Nhị thức Newton

Ví dụ 5: Tính tổng: S=\frac{1}{2}C_{n}^{0}-\frac{1}{4}c_{n}^{1}+\frac{1}{6}C_{n}^{3}-\frac{1}{8}C_{n}^{4}+...+\frac{\left( -1 \right)}{2\left( n+1 \right)}C_{n}^{n}

Hướng dẫn giải

Ta có: S=\frac{1}{2}\left( C_{n}^{0}-\frac{1}{2}c_{n}^{1}+\frac{1}{3}C_{n}^{3}-\frac{1}{4}C_{n}^{4}+...+\frac{\left( -1 \right)}{n+1}C_{n}^{n} \right)

Vì \frac{{{\left( -1 \right)}^{k}}}{k+1}C_{n}^{k}=\frac{{{\left( -1 \right)}^{k}}}{k+1}C_{n+1}^{k+1}

\begin{matrix} \Leftrightarrow S = \dfrac{1}{{2\left( {n + 1} \right)}}\sum\limits_{k = 0}^n {{{\left( { - 1} \right)}^k}C_{n + 1}^{k + 1}} \hfill \\ = \dfrac{{ - 1}}{{2\left( {n + 1} \right)}}\left( {\sum\limits_{k = 0}^{n + 1} {{{\left( { - 1} \right)}^k}C_{n + 1}^k - C_{n + 1}^0} } \right) \hfill \\ = \dfrac{1}{{2\left( {n + 1} \right)}} \hfill \\ \end{matrix}

Câu trắc nghiệm mã số: 9408,9409,9406
  • 4.775 lượt xem
1 Bình luận
Sắp xếp theo
🖼️
Xóa Gửi bình luận
  • Le Tuan Anh
    Le Tuan Anh

    Hay quá ạ 😍
    Thích Phản hồi 06/05/23

Toán 11