Hai mặt phẳng song song
I. Định nghĩa
Định nghĩa
Hai mặt phẳng (α) và (β) gọi là song song với nhau nếu chúng không có điểm chung.
Kí hiệu: (α) // (β) hay (β) // (α).
Hình vẽ minh họa
II. Tính chất
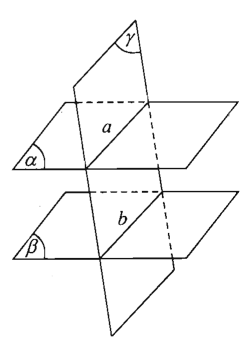
Định lí 1
Nếu mặt phẳng (α) chứa hai đường thẳng a, b và a, b cùng song song với mặt phẳng (β) thì (α) // (β).
Hình vẽ minh họa

Định lí 2
Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.
Hình vẽ minh họa
Hệ quả 1
Nếu đường thẳng d song song với mặt phẳng (α) thì qua d có duy nhất một mặt phẳng song song với (α).
Hệ quả 2
Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.
Hệ quả 3
Cho điểm A không nằm trên mặt phẳng (α). Mọi đường thẳng đi qua A và song song với (α) đều nằm trong mặt phẳng qua A và song song với (α).
Hình ảnh minh họa
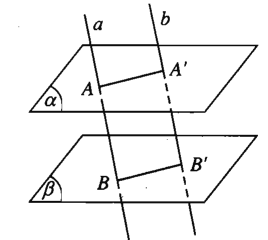
Định lí 3
Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
Hình vẽ minh họa
Ví dụ: Cho hình chóp S.ABCD đáy ABCD là hình bình hành tâm H. Mặt phẳng (P) đi qua H và song song với (SAB). Tìm giao tuyến của mặt phẳng (P) và mặt phẳng (ABCD).
Hướng dẫn giải
Hình vẽ minh họa
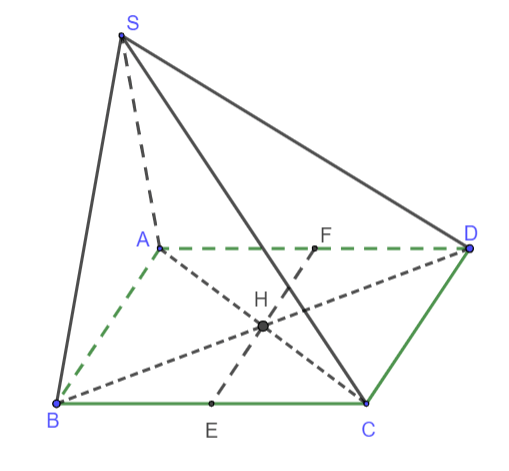
Giao tuyến của mặt phẳng (P) và mặt phẳng (ABCD).

Với 
Hệ quả
Hai mặt phẳng song song chắn hai cát tuyến song song những đoạn thẳng bằng nhau.
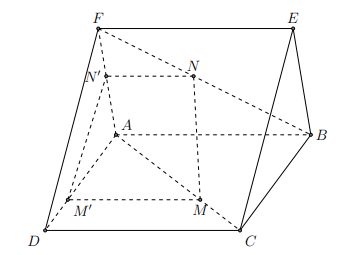
Ví dụ: Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng phân biệt. Trên các đường chéo AC và BF lần lượt lấy các điểm M, N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M và N lần lượt cắt AD và AF tại M’ và N’. Chứng minh:
a) (ADF) // (BCE)
b) M’N’ // DF
c) (DEF) // (MM’N’N) và MN // (DEF).
Hướng dẫn giải
Hình vẽ minh họa
a) Ta có: 
Tương tự: 
Mà ![]()
=> ![]()
b) Ta có: ABCD và ABEF là các hình vuông nên AC = BF. Khi đó:
MM’ // CD => ![]()
NN’ // AB => ![]()
=> ![]()
c) Từ chứng minh trên ra suy ra: DF // (MM’N’N)
Mặt khác 
Mà ![]()
![]()
Vì 
III. Định lí Ta – Lét (Thalès)
Định lí Ta – lét
Ba mặt phẳng đôi một song song chắn hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.
Hình ảnh minh họa
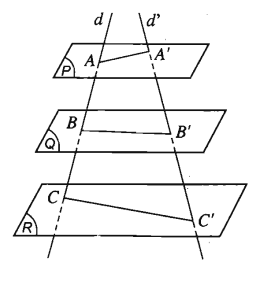
Chú ý: Nếu hai cát tuyến d và d’ cắt ba mặt phẳng song song (P) // (Q) // (R) lần lượt tại các giao điểm A, B, C và A’, B’, C’ thì ![]()
Ví dụ: Cho hình hộp ABCD.A’B’C’D’. Trên ba cạnh AB, DD’, C’B’ lần lượt lấy ba điểm M, N, P không trùng với các đỉnh sao cho ![]() (*). Chứng minh rằng hai mặt phẳng (MNP) và (AB’D’) song song với nhau.
(*). Chứng minh rằng hai mặt phẳng (MNP) và (AB’D’) song song với nhau.
Hướng dẫn giải
Hình vẽ minh họa

Từ (*) ta suy ra được: ![]()
Theo Định lý Ta - lét đảo, ta có ba đường thẳng MP, AB’, BC’ cùng song song với một mặt phẳng (α) cố định.
Ta có thể lấy (α) là mặt phẳng qua C và song song với AB’, BC’.
Do (α) // BC’, mà BC’ // AD’ và AD’ ⊄ (α), nên (α) // AD’, (AD’ ⊄ (α) vì (α) // AB’, nghĩa là (α) không thể chứa điểm A).
Ta có: 
=> (AB’D’) // (α)
Vậy (α) là mặt phẳng qua C, song song với (AB’D’).
Từ giả thiết (*), ta suy ra được ![]()
Theo Định lý Ta - lét đảo, ta có ba đường thẳng AD’, MN, BD cùng song song với một mặt phẳng (β) cố định.
Ta có thể lấy (β) là mặt phẳng qua C và song song với AD’, BD.
Do (β) // BD, mà BD // B’D’ và B’D’ ⊄ (β), nên (β) // B’D’, (B’D’ ⊄ (β) vì (β) // AD’, nghĩa là (β) không thể chứa điểm D’).
Ta có: 
=> (AB’D’) // (β)
Vậy (β) là mặt phẳng qua C, song song với (AB’D’), suy ra (β) ≡ (α)
Ta có: 
=> (MNP) // (α)
Lại có (AB’D’) // (α), (AB’D’) và (MNP) phân biệt, suy ra (MNP) // (AB’D’).
IV. Hình lăng trụ và hình hộp
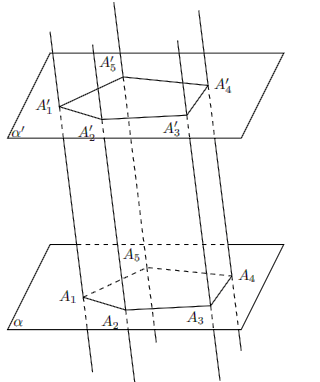
Định nghĩa
Cho hai mặt phẳng (α) // (α’). Trong (α) cho đa giác lồi A1A2A3 …. An.
Qua các điểm A1, A2, A3, …., An ta dựng các đường song song với nhau và cắt (α’) tại A’1A’2A’3 …. A’n.
Hình tạo thành bởi hai đa giác A1A2A3 …. An và A’1A’2A’3 …. A’n cùng với các hình bình hành A1A2A’2A’1, A2A3A’3A’2, …, AnA1A’1A’n được gọi là hình lăng trụ và được kí hiệu bởi A1A2A3 …. An.A’1A’2A’3…. A’n.
Hình vẽ minh họa
Đặc điểm của hình lăng trụ
- Hai đa giác A1A2A3 …. An và A’1A’2A’3 …. A’n được gọi là mặt đáy (bằng nhau) của hình lăng trụ.
- Các đoạn thẳng A1A’1, A2A’2, … , AnA’n gọi là các cạnh bên của hình lăng trụ.
- Các hình bình hành A1A2A’2A’1, A2A3A’3A’2, …, AnA1A’1A’n được gọi là các mặt bên của hình trụ.
- Các đỉnh của hai đa giác đáy là các đỉnh của hình lăng trụ.
Tính chất của hình lăng trụ
- Các mặt bên của hình lăng trụ thì song song và bằng nhau.
- Các mặt bên của hình lăng trụ đều là hình bình hành.
- Hai đáy của hình lăng trụ là hai đa giác bằng nhau.
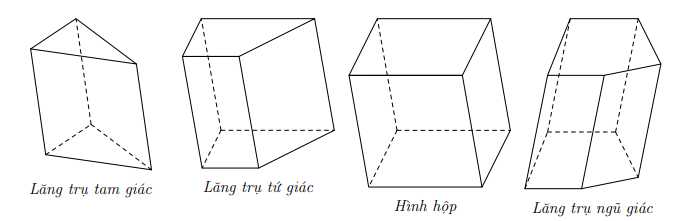
- Hình lăng trụ có đáy là tam giác được gọi là hình lăng trụ tam giác.
- Hình lăng trụ có đáy là hình bình hành là hình hộp.
- Người ta gọi tên hình lăng trụ theo đáy của nó như sau:
V. Hình chóp cụt
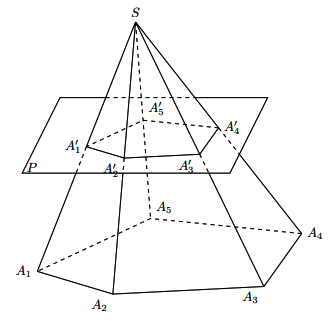
Định nghĩa
Cho hình chóp S.A1A2A3 …. An. Một mặt phẳng (P) song song với mặt đáy của hình chóp không đi qua đỉnh lần lượt cắt các cạnh SA1, SA2, …., SAn tại A’1, A’2, A’3, …. , A’n. Hình tạo thành bởi đa giác A’1A’2A’3 …. A’n, A1A2A3 …. An và các tứ giác A1A2A’2A’1, A2A3A’3A’2, …, AnA1A’1A’n gọi là hình chóp cụt.
Hình vẽ minh họa
Đặc điểm của hình chóp cụt
- Đáy A1A2A3 …. An của hình chóp gọi là đáy lớn của hình chóp cụt.
- Thiết diện A’1A’2A’3 …. A’n của hình chóp và (P) gọi là đáy nhỏ của hình chóp cụt.
- Ta gọi tên hình chóp cụt theo đa giác đáy của nó (chóp cụt tam giác, tứ giác, …)
Tính chất của hình chóp cụt
- Hai đáy của hình chóp cụt là hai đa giác có cạnh tương ứng song song và tỉ lệ giữa các cặp có cạnh tương ứng bằng nhau.
- Các mặt bên là hình thang
- Các đường thẳng chứa các cạnh bên đồng quy tại 1 điểm.
-
Chương 1: Hàm số lượng giác và phương trình lượng giác
-
Chương 2: Tổ hợp - xác suất
-
Chương 3: Dãy số - Cấp số cộng và cấp số nhân
-
Chương 4: Giới hạn
-
Chương 5: Đạo hàm
-
Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng
-
Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
-
Chương 3: Vectơ trong không gian. Quan hệ vuông góc trong không gian







