Lớp 11 Toán 11 (sách cũ)

Luyện tập Phép đồng dạng

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 15 câu
  • Điểm số bài kiểm tra: 15 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Nhận biết
    Tìm mệnh đề sai

    Mệnh đề nào sau đây là sai?

    Hướng dẫn:

    Phép đồng dạng có tỉ số khác ±1 thì không bảo toàn khoảng cách giữa hai điểm nên không phải là phép dời hình

  • Câu 2: Thông hiểu
    Chọn các mệnh đề sai

    Có bao nhiêu mệnh đề sai trong các mệnh đề sau?

    P: Phép dời hình là một phép đồng dạng.

    Q: Phép vị tự là một phép đồng dạng.

    R: Phép đồng dạng là một phép dời hình.

    Hướng dẫn:

    Phép dời hình là một phép đồng dạng.” là mệnh đề đúng.

    “Phép vị tự là một phép đồng dạng.” là mệnh đề đúng.

    “Phép đồng dạng là một phép dời hình.” là mệnh đề sai. 

    Vậy có 1 mệnh đề sai trong các mệnh đề đã cho.

  • Câu 3: Thông hiểu
    Xác định mệnh đề sai

    Cho tam giác ABC và A'B'C' đồng dạng với nhau theo tỉ số k. Mệnh đề nào sau đây là sai?

    Hướng dẫn:

    Vì hai tam giác đồng dạng thì các góc tương ứng luôn bằng nhau

    => k là tỉ số hai góc tương ứng

  • Câu 4: Thông hiểu
    Xác định k

    Mọi phép dời hình cũng là phép đồng dạng với tỉ số k bằng: 

    Hướng dẫn:

    Phép dời hình là phép đồng dạng tỉ số k = 1.

  • Câu 5: Thông hiểu
    Tìm mệnh đề sai

    Mệnh đề nào sau đây là sai?

    Hướng dẫn:

    Phép đồng dạng biến đường thẳng thành đường thẳng song song hoặc trùng hoặc cắt với nó.

  • Câu 6: Vận dụng
    Xác định ảnh của IGHF qua phép đồng dạng

    Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm I biến tứ giác IGHF thành:

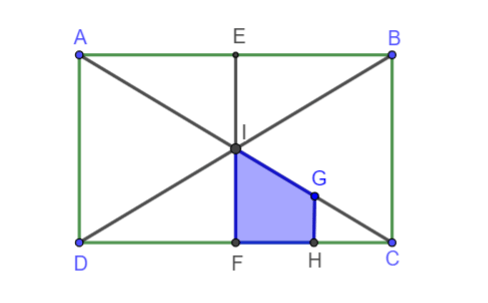
    Xác định ảnh của IGHF qua phép đồng dạng

    Hướng dẫn:

    Ta có:

    \begin{matrix} {V_{\left( {C;2} ight)}}\left( {IGHF} ight) = \left( {AIFD} ight) \hfill \\ {D_I}\left( {AIFD} ight) = CIEB \hfill \\ \end{matrix}

  • Câu 7: Vận dụng
    Tìm ảnh của điểm M

    Trong mặt phẳng tọa độ Oxy phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số k=\dfrac{1}{2} và phép đối xứng trục Ox biến điểm M(4;2) thành điểm có tọa độ là:

    Hướng dẫn:

    Phép vị tự tâm O, tỉ số k=\dfrac{1}{2} biến điểm M(4;2) thành điểm có tọa độ M'(x'; y')

    => \overrightarrow {OM'} = k\overrightarrow {OM}

    => \left\{ {\begin{array}{*{20}{c}} {x' - 0 = \dfrac{1}{4}\left( {4 - 0} ight) = 2} \\ {y' - 0 = \dfrac{1}{2}\left( {2 - 0} ight) = 1} \end{array}} ight.

    Phép đối xứng qua trục Ox biến điểm M'(2; 1) thành điểm M'(2; -1).

  • Câu 8: Vận dụng
    Tìm mệnh đề sai

    Cho hình thoi ABCD tâm O. Gọi E, F, M, N lần lượt là trung điểm các cạnh AB, CD, BC, AD. P là phép đồng dạng biến tam giác OCF thành tam giác CAB. Tìm mệnh đề sai trong các mệnh đề sau:

    Hướng dẫn:

     Đáp án A

    \begin{matrix} {D_O}(\Delta OCF) = \Delta OAE \hfill \\ {V_{(A;2)}}(\Delta OAE) = \Delta CAB \hfill \\ \end{matrix}

    Đáp án B

    \begin{matrix} {D_{AC}}(\Delta OCF) = \Delta OCM \hfill \\ {V_{(C;2)}}(\Delta OCM) = \Delta ACB \hfill \\ \end{matrix}

    Đáp án C

    \begin{matrix} {V_{(C;2)}}(\Delta OCF) = \Delta ACD \hfill \\ {D_O}(\Delta ACD) = \Delta CAB \hfill \\ \end{matrix}

    Đáp án D

    \begin{matrix} {D_{BD}}(\Delta OCF) = \Delta OAN \hfill \\ {V_{(O; - 1)}}(\Delta OAN) = \Delta OCM \hfill \\ \end{matrix}

    Vậy phép đồng dạng P được hợp thành bởi phép đối xứng trục BD và phép vị tự tâm O, tỉ số k = -1 không biến tam giác OCF thành tam giác CAB.

  • Câu 9: Vận dụng
    Xác định ảnh của điểm M

    Cho điểm I(2;1) điểm M(-1;0) phép đồng dạng hợp thành bởi phép vị tự tâm I tỉ số k = -2 và phép đối xứng trục Ox biến M thành M’' có tọa độ.

    Hướng dẫn:

    Phép vị tự tâm I với tỉ số k = -2 biến điểm M thành điểm M'(x'; y')

    => \overrightarrow {IM'} = - 2\overrightarrow {IM}

     \begin{matrix} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x' - 2 = - 2\left( { - 1 - 2} ight) = 6} \\ {y' - 1 = - 2\left( {0 - 1} ight) = 2} \end{array}} ight. \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x' = 8} \\ {y' = 3} \end{array}} ight. \Leftrightarrow M'\left( {8;3} ight) \hfill \\ \end{matrix}

    Phép đối xứng qua trục Ox biến điểm M'(8; 3) thành điểm M''(8; -3).

  • Câu 10: Vận dụng
    Xác định đường thẳng d'

    Trong mặt phẳng tọa độ Oxy, phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số k = 3 và phép đối xứng trục Ox, biến đường thẳng d: x - y - 1 = 0 thành đường thẳng d’ có phương trình.

    Hướng dẫn:

    Phương trình đường thẳng d: x - y - 1= 0

    Lấy M(x; y) thuộc d

    Phép vị tự tâm O(0; 0) tỉ số k = 3 biến điểm M thành M’(x’; y’) thì

    \begin{matrix}\overrightarrow {OM'} = 3\overrightarrow {OM} \hfill \\\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x' = 3x} \\{y' = 3y}\end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = \dfrac{1}{3}x'} \\{y = \dfrac{1}{3}y'}\end{array}} ight. \hfill \\\end{matrix}

    Phép đối xứng trục Ox biến M’(x’; y’) thành M’’(x’’; y’’)

    \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x'' = x'} \\{y'' = - y'}\end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = \dfrac{1}{3}x''} \\{y = \dfrac{1}{3}y''}\end{array}} ight.

    Thay vào phương trình d ta được:

    Hay x’’ + y’’ - 3 = 0

    Vậy phương trình đường thẳng d’: x + y - 3 = 0.

  • Câu 11: Vận dụng
    Tìm ảnh của điểm M

    Trong mặt phẳng tọa độ Oxy cho điểm M(2; 4). Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k=\frac{1}{2} và phép đối xứng qua trục Oy sẽ biến M thành điểm nào trong các điểm sau:

    Hướng dẫn:

    Giả sử M'\left( {x';y'} ight) = {V_{\left( {0;\frac{1}{2}} ight)}}\left( M ight)

    \begin{matrix} \Leftrightarrow \overrightarrow {OM'} = \dfrac{1}{2}\overrightarrow {OM} \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x = 1} \\ {y = 2} \end{array}} ight. \hfill \\ \Rightarrow M'\left( {1;2} ight)\mathop \to \limits^{{D_{Oy}}} M''\left( { - 1;2} ight) \hfill \\ \end{matrix}

  • Câu 12: Vận dụng
    Viết phương trình đường thẳng d'

    Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình x + y - 2 = 0. Viết phương trình đường thẳng d' là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm I(-1;-1) tỉ số k=\frac{1}{2} và phép quay tâm O góc -45^{\circ}

    Hướng dẫn:

    Gọi d1 là ảnh của d qua phép vị tự tâm I (−1; −1) tỉ sốk = \frac{1}{2}

    Vì d1 song song hoặc trùng với d nên phương trình của nó có dạng x + y + c = 0.

    Lấy M (1; 1) thuộc d.

    Gọi M'\left( {x';y'} ight) = {V_{\left( {I;\frac{1}{2}} ight)}}\left( M ight)

    \begin{matrix}\Leftrightarrow \overrightarrow {IM'} = \dfrac{1}{2}\overrightarrow {IM} \hfill \\\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x' + 1 = \dfrac{1}{2}\left( {1 + 1} ight)} \\{yY + 1 = \dfrac{1}{2}\left( {1 + 1} ight)}\end{array}} ight. \hfill \\\Rightarrow M'\left( {0;0} ight) \in {d_1} \hfill \\\end{matrix}

    Vậy phương trình của d1 là x + y = 0.

    Ảnh của d1 (đường phân giác góc phần tư thứ hai) qua phép quay tâm O góc −450 là đường thẳng Oy. Vậy phương trình của d 0 là x = 0.

  • Câu 13: Vận dụng
    Tìm ảnh của đường tròn (C)

    Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có phương trình (x-2)^{2}+(y-2)^{2}=4 Phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k=\frac{1}{2} và phép quay tâm O góc 90^{\circ} sẽ biến (C) thành đường tròn nào trong các đường tròn sau:

    Hướng dẫn:

    Đường tròn (C) có tâm I (2; 2), bán kính R = 2.

    Suy ra phép vị tự {V_{\left( {O;\frac{1}{2}} ight)}} biến (C) thành (C’) tâm I’(1; 1), bán kính R’ = 1.

    Phép quay Q(O; 90o) biến (C’) thành (C’’) có tâm I’’(−1; 1), bán kính R’’ = R’ = 1.

    Vậy phương trình đường tròn (C’’) là (x + 1)2 + (y − 1)2 = 1.

  • Câu 14: Thông hiểu
    Tính độ dài A'B'

    Trong mặt phẳng tọa độ Oxy cho hai điểm A(-2; -3) và B(4; 1). Phép đồng dạng tỉ số k=\frac{1}{2} biến điểm A thành A', biến điểm B thành B'. Tính độ dài A'B'.

    Hướng dẫn:

    Phép đồng dạng tỉ số k = \frac{1}{2} điểm A thành A', biến điểm B thành B'nên ta có:

    A'B' = \frac{1}{2}AB = \frac{{\sqrt {{{\left( {4 + 2} ight)}^2} + {{\left( {1 + 3} ight)}^2}} }}{2} = \frac{{\sqrt {52} }}{2}

  • Câu 15: Thông hiểu
    Tính tỉ số đồng dạng k

    Trong mặt phẳng tọa độ Oxy, cho hai đường tròn (C) và (C') có phương trình x^{2}+y^{2}-4y-5=0 và x^{2}+y^{2}-2x+2y-14=10. Gọi (C') là ảnh của (C) qua phép đồng dạng tỉ số k, khi đó giá trị k là:

    Hướng dẫn:

     Đường tròn (C) có bán kính của R = 3. Đường tròn (C') có bán kính R' = 4

    Suy ra tỉ số đồng dạng k = \frac{{R'}}{R} = \frac{4}{3}

0/15
15 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (7%):
    2/3
  • Thông hiểu (40%):
    2/3
  • Vận dụng (53%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 5 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11

Đăng nhập