Lớp 11 Toán 11

Phép vị tự

1. Phép vị tự

Định nghĩa

Cho điểm O và số k\neq 0. Phép biến hình biến mỗi điểm M thành điểm M'' sao cho: \overrightarrow {OM} = k\overrightarrow {OM'} được gọi là phép vị tự tâm O tỉ số k. 

Phép vị tự tâm O tỉ số k thường được kí hiệu là V_{(O,k)}.

Hình vẽ minh họa

Phép vị tự

Nhận xét

  • Phép vị tự biến tâm vị tự thành chính nó.
  • Khi k = 1, phép vị tự là đồng nhất.
  • Khi k = −1, phép vị tự là phép đối xứng tâm.
  • M' = {V_{\left( {O;k} \right)}}\left( M \right) \Leftrightarrow M = {V_{\left( {O;\dfrac{1}{k}} \right)}}\left( {M'} \right)

2. Tính chất của phép vị tự

Tính chất 1

Nếu phép vị tự tỉ số k biến hai điểm M, N thành M', N' thì \vec{M'N'} =k\vec{MN} và M'N' = \left| k \right|MN.

Tính chất 2

Phép vị tự tỉ số k:

  • Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự các điểm ấy.
  • Biến một đường thẳng thành một đường thẳng song song hoặc trùng với đường thẳng ấy, biến một tia thành một tia, biến một đoạn thẳng thành một đoạn thẳng.
  • Biến đường tròn thành đường tròn có cùng bán kính.
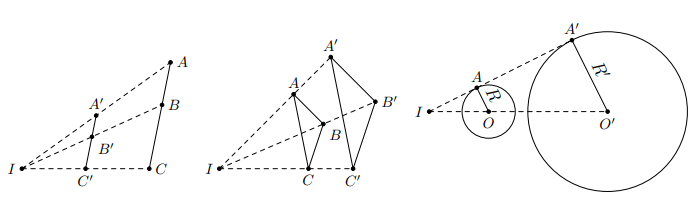
  • Biến một tam giác thành một tam giác đồng dạng với nó, một góc thành góc bằng nó.

Hình vẽ minh họa

Phép vị tự

Ví dụ: Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x + 2y − 6 = 0. Hãy viết phương trình của đường thẳng d' là ảnh của d qua phép vị tự tâm O tỉ số k = −2.

Hướng dẫn giải

Do d' song song hoặc trùng với d nên d’: 3x + 2y + C = 0

Lấy M(0; 3) ∈ d.

Gọi M’(x’; y’) là ảnh của M qua phép vị tự tâm O tỉ số k = −2.

Ta thấy rằng \overrightarrow {OM} = \left( {0;3} \right);\overrightarrow {OM'} = \left( {x;y} \right) = - 2\overrightarrow {OM}

Ta có: \left\{ {\begin{array}{*{20}{l}} {x{\text{ '}} = {\text{ }}0} \\ {y' = - 2.3 = - 6} \end{array}} \right.

Do M’ ∈ d’ nên 2(−6) + C = 0

=> C = 12

Từ đó phương trình d’: 3x + 2y + 12 = 0.

3. Cách tìm tâm vị tự của hai đường tròn

Cho hai đường tròn (I, R) và (I’, R’).

a) Trường hợp I trùng với I'.

Hình vẽ minh họa

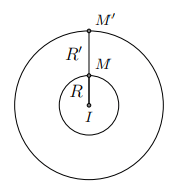
Phép vị tự

Phép vị tự tâm I, tỉ số \frac{{R'}}{R} và phép vị tự tâm I, tỉ số -\frac{{R'}}{R} biến đường tròn (I, R) thành đường tròn (I, R’).

b) Trường hợp I khác I' và R khác R’.

Hình vẽ minh họa

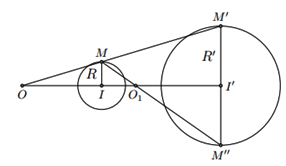
Phép vị tự

Lấy M bất kì thuộc (I, R), đường thẳng qua I' song song với IM cắt (I’, R’) tại M’ và M’’.

Giả sử M, M’ nằm cùng phía đối với đường thẳng II’ còn M, M’’ nằm khác phía với đường thẳng II’.

Giả sử đường thằng M, M’ cắt II’ tại O nằm ngoài đoạn thẳng II’, còn đường thằng M, M’’ cắt II’ tại O_1 nằm ngoài đoạn thẳng II’.

Khi đó phép vị tự tâm O, tỉ số \frac{{R'}}{R} và phép vị tự tâm O_1, tỉ số -\frac{{R'}}{R} biến đường tròn (I, R) thành đường tròn (I’, R’).

Ta gọi O là tâm vị tự ngoài, còn O_1 là tâm vị tự trong của hai đường tròn nói trên.

c) Trường hợp I khác I' và R = R’.

Hình vẽ minh họa

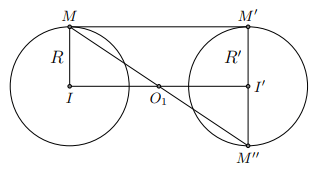
Phép vị tự

Khi đó MM’ // II’ nên chỉ có phép vị tự tâm O_1, tỉ số k=-\frac{{R'}}{R}=-1 biến đường tròn (I, R) thành đường tròn (I’, R’). Nó chính là phép đối xứng tâm O_1.

Ví dụ: Cho hai đường tròn (O, 3R) và (O’, R) nằm ngoài nhau. Tìm phép vị tự biến (O, 3R) thành (O’, R).

Hướng dẫn giải

Hình ảnh minh họa

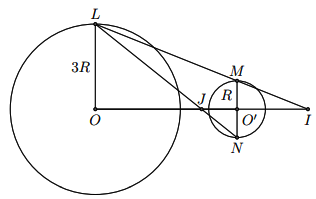
Phép vị tự

Lấy L bất kì thuộc (O, 3R), đường thẳng qua O' song song với OL cắt (O’, R) tại M và N.

Hai đường thằng LM và LN cắt OO’ lần lượt tại I, J.

Khi đó phép vị tự {V_{\left( {I;\frac{1}{3}} \right)}} và {V_{\left( {J; - \frac{1}{3}} \right)}} biến (O, 3R) và (O’, R).

Câu trắc nghiệm mã số: 9795,9796,9797
  • 1.356 lượt xem

Nội dung cùng chủ đề

Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11