Lớp 11 Toán 11 (sách cũ)

Khoảng cách

1. Khoảng cách từ một điểm đến một đường thẳng

Hình vẽ minh họa

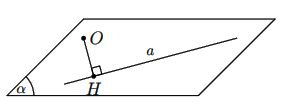
Khoảng cách

Cho một điểm O và một đường thẳng. Trong (O, a) gọi H là hình chiếu vuông góc của O trên a. Khi đó khoảng cách OH được gọi là khoảng cách từ điểm O đến a, kí hiệu là: d(O, a) = OH.

Ví dụ: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Chứng minh rằng khoảng cách từ điểm B, C, D, A’, B’, D’ đến đường chéo AC’ đều bằng nhau. Tính khoảng cách đó.

Hướng dẫn giải

Hình vẽ minh họa

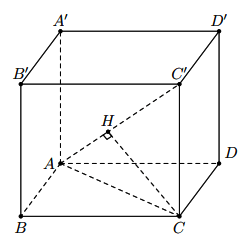
Khoảng cách

Ta có:

ΔBAC’ = ΔCAA’ = ΔDAC’ = ΔA’AC = ΔB’C’A = ΔD’C’A chung đáy AC’ nên khoảng cách từ B, C, D, A’, B’, D’ đến đường chéo AC’ đều bằng nhau.

Hạ CH ⊥ AC’ ta được:

\frac{1}{{C{H^2}}} = \frac{1}{{A{C^2}}} + \frac{1}{{CC{'^2}}} \Rightarrow CH = \frac{{a\sqrt 6 }}{3}

2. Khoảng cách từ một điểm đến một mặt phẳng

Hình vẽ minh họa

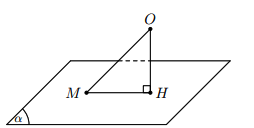
Khoảng cách

Cho mặt phẳng (α) và một điểm O, gọi H là hình chiếu vuông góc của điểm O trên mặt phẳng (α). Khi đó khoảng cách OH được gọi là khoảng cách từ điểm O đến mặt phẳng (α), kí hiệu d(O, (α)) = OH.

Chú ý: OH \leqslant OM,\forall M \in \left( \alpha \right)

Tính chất 1: Nếu đường thẳng d song song với mặt phẳng (P) thì khoảng cách từ mọi điểm trên đường thẳng d đến mặt phẳng (P) là như nhau.

Tính chất 2: Nếu \overrightarrow {AM} = k\overrightarrow {BM} thì d\left( {A,\left( P \right)} \right) = \left| k \right|d\left( {B,\left( P \right)} \right), trong đó (P) là mặt phẳng đi qua M.

Ví dụ: Cho hình chóp S.ABC có SA = a\sqrt 3, SA ⊥ (ABC), tam giác ABC vuông tại B và AB = a. Tính khoảng cách từ A đến (SBC).

Hướng dẫn giải

Hình vẽ minh họa

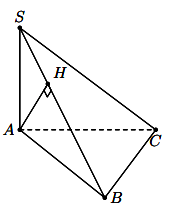
Khoảng cách

Ta có: \left\{ {\begin{array}{*{20}{l}} {SA \bot \left( {ABC} \right)} \\ {SA \subset \left( {SAB} \right)} \end{array}} \right. \Rightarrow \left( {SAB} \right) \bot \left( {ABC} \right)

Mà \left\{ {\begin{array}{*{20}{l}} {\left( {SAB} \right) \cap \left( {ABC} \right) = AB} \\ {AB \bot BC} \end{array}} \right.

=> BC ⊥ (SAB)

Do BC ⊂ (SBC) => (SBC) ⊥ (SAB)

Kẻ AH ⊥ SB với H ∈ SB

Do (SAB) ∩ (SBC) = SB => AH ⊥ (SBC)

=> d(A, (SBC)) = AH

Do SA ⊥ (ABC) => SA ⊥ AB khi đó ta có:

\begin{matrix} \dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{B^2}}} \hfill \\ \Rightarrow \dfrac{1}{{A{H^2}}} = \dfrac{1}{{3{a^2}}} + \dfrac{1}{{{a^2}}} = \dfrac{4}{{3{a^2}}} \hfill \\ \Rightarrow AH = \dfrac{{a\sqrt 3 }}{2} \hfill \\ \Rightarrow d\left( {A;SBC} \right) = AH = \dfrac{{a\sqrt 3 }}{2} \hfill \\ \end{matrix}

Câu trắc nghiệm mã số: 16326,12694

3.Khoảng cách từ một đường thẳng tới một mặt phẳng song song

Hình vẽ minh họa

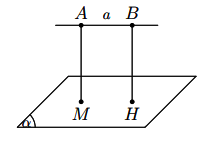
Khoảng cách

Cho đường thẳng a song song với (α). Khoảng cách giữa đường thẳng a và mặt phẳng (α) là khoảng cách từ một điểm bất kì của a đến mặt phẳng (α). Kí hiệu: d(a, (α))

Chú ý: d\left( {a;\left( \alpha \right)} \right) = d\left( {A,\left( \alpha \right)} \right),\forall A \in a

4. Khoảng cách giữa hai mặt phẳng song song

Hình vẽ minh họa

Khoảng cách

Cho hai mặt phẳng (α) và (β) song song với nhau, khoảng cách từ một điểm bất kì trên mặt phẳng này đến mặt phẳng kia được gọi là khoảng cách giữa hai mặt phẳng (α) và (β).

d\left( {\left( \alpha \right);\left( \beta \right)} \right) = d\left( {M;\left( \beta \right)} \right) = d\left( {N,\left( \alpha \right)} \right),M \in \left( \alpha \right),N \in \left( \beta \right)

Ví dụ: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng a, mặt bên (SBC) vuông góc với đáy. Gọi M, N, P theo thứ tự là trung điểm AB, SA, AC. Tính khoảng cách giữa hai mặt phẳng (MNP) và (SBC).

Hướng dẫn giải

Hình vẽ minh họa

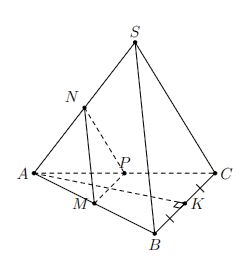
Khoảng cách

Ta chứng minh được (MNP) // (SBC)

=> d((MNP), (SBC)) = d(P, (SBC))

Giả sử AP ∩ (SBC) = C

=> d\left( {P;\left( {SBC} \right)} \right) = \frac{{AP}}{{AC}}.d\left( {A,\left( {SBC} \right)} \right) = \frac{1}{2}d\left( {A,\left( {SBC} \right)} \right)

Gọi K là trung điểm của BC.

Tam giác ABC đều => AK ⊥ BC

Do (ABC) ⊥ (SBC) theo giao tuyến BC => AK ⊥ (SBC)

=> d\left( {A,\left( {SBC} \right)} \right) = AK = \frac{{a\sqrt 3 }}{2}{\text{ }}

Vậy d\left( {\left( {MNP} \right),\left( {SBC} \right)} \right) = \frac{{a\sqrt 3 }}{4}

Câu trắc nghiệm mã số: 16333

5. Đường thẳng vuông góc chung và khoảng cách giữa hai đường thẳng chéo nhau

Hình vẽ minh họa

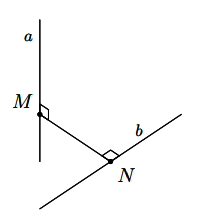
Khoảng cách

Định nghĩa

a) Đường thẳng Δ cắt hai đường thẳng chéo nhau a, b và cùng vuông góc với mỗi đường thẳng ấy được gọi là đường vuông góc chung a và b.

b) Nếu đường thẳng vuông góc chung Δ cắt hai đường chéo nhau a và b lần lượt tại M, N thì độ dài đoạn MN gọi là khoảng cách giữa hai đường thẳng chéo nhau a và b.

Ví dụ: Cho hình lăng trụ đứng ABC.A’B’C; có đáy ABC là tam giác vuông tại A với AB = a, AC = 2a; cạnh bên AA’ = 2a. Hãy dựng và tính độ dài đoạn vuông góc chung của hai đường thẳng BC’ và AA’.

Hướng dẫn giải

Hình vẽ minh họa

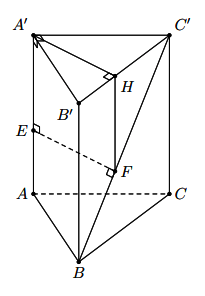
Khoảng cách

Ta có AA’ // BB’ => AA’// (BB’C’C)

Vì (A’B’C’) ⊥ (BB’C’C) theo giao tuyến B’C’

=> Trong mặt phẳng (A’B’C’), kẻ A’H ⊥ B’C’ tại H, ta có A’H ⊥ (BB’C’C)

=> A’H ⊥ BC’

Trong mặt phẳng (B’C’C), kẻ HF // AA’ (F ∈ BC’)

Trong mặt phẳng (HF, AA’), kẻ FE // A’H (E ∈ AA’) => FE ⊥ BC’

Ta có: AA’ ⊥ (A’B’C’) => AA’ ⊥ A’H => AA’ ⊥ FE.

Do đó EF là đoạn vuông góc chung của AA’ và BC’

Trong tam giác vuông A’B’C’ ta có:

\begin{matrix} \dfrac{1}{{A'H{'^2}}} = \dfrac{1}{{A'B{'^2}}} + \dfrac{1}{{A'C{'^2}}} \hfill \\ = \dfrac{1}{{{a^2}}} + \dfrac{1}{{4{a^2}}} = \dfrac{5}{{4{a^2}}} \hfill \\ \Rightarrow EF = A'H = \dfrac{{2a\sqrt 5 }}{5} \hfill \\ \Rightarrow d\left( {AA';BC'} \right) = \dfrac{{2a\sqrt 5 }}{5} \hfill \\ \end{matrix}

Câu trắc nghiệm mã số: 16324,16322,16321
  • 6 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 11