Vectơ trong không gian

1. Các định nghĩa

a) Vectơ là một đoạn thẳng có hướng (có phân biệt điểm đầu và điểm cuối).

b) Vectơ không là vectơ có điểm đầu và điểm cuối trùng nhau. Ký hiệu .

c) Ký hiệu vectơ: (điểm đầu là A, điểm cuối là B) hay

d) Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Độ dài của ký hiệu là , độ dài của ký hiệu là .

e) Giá của vectơ là đường thẳng đi qua điểm đầu và điểm cuối của vectơ đó.

f) Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

g) Hai vectơ cùng phương thì cùng hướng hoặc ngược hướng.

h) Hai vectơ bằng nhau là hai vectơ cùng hướng và có cùng độ dài. Tức là

i) Hai vectơ đối nhau là hai vectơ ngược hướng nhưng vẫn có cùng độ dài.

j) Các phép toán cộng, trừ, nhân vectơ với một số được định nghĩa tương tự trong mặt phẳng.

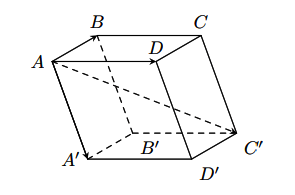
Ví dụ: Cho hình hộp ABCD.A’B’C’D’. Hãy xác định các vectơ (khác ) có điểm đầu, điểm cuối là các đỉnh của hình hộp ABCD.A’B’C’D’ và

a) cùng phương với

b) cùng phương

Hướng dẫn giải

a) Các vectơ có điểm đầu, điểm cuối là các đỉnh của hình hộp cùng phương với là

b) Các vectơ có điểm đầu, điểm cuối là các đỉnh của hình hộp cùng phương với là

2. Các quy tắc tính toán với vectơ

a) Quy tắc ba điểm

b) Quy tắc hình bình hành

c) Quy tắc hình hộp

3. Một số hệ thức vectơ trọng tâm cần nhớ

a) I là trung điểm của đoạn thẳng AB khi đó

(với O là một điểm bất kỳ).

b) G là trọng tâm của tam giác ABC khi đó

(với O là một điểm bất kỳ, M là trung điểm cạnh BC).

c) G là trọng tâm của tứ diện ABCD khi đó

(với điểm O bất kỳ, A’ là trọng tâm của ΔBCD)

(với M, N là trung điểm 1 cặp cạnh đối diện).

d) và cùng phương

e)  và cùng hướng

f)  và ngược hướng

g) Ba điểm A, B, C thẳng hàng

4. Điều kiện đồng phẳng của ba vectơ

Định nghĩa

Trong không gian, ba vectơ được gọi là đồng phẳng nếu giá của chúng cùng song song với một mặt phẳng nào đó.

Hệ quả 1

Nếu có một mặt phẳng chứa vectơ này đồng thời song song với giá của hai vectơ kia thì ba vectơ đó đồng phẳng.

Định lí 1 (Điều kiện để ba vectơ đồng phẳng)

Trong không gian cho hai vectơ và không cùng phương và vectơ . Khi đó và đồng phẳng khi và chỉ khi tồn tại cặp số (m; n) sao cho (cặp số (m; n) nêu trên là duy nhất).

Bốn điểm phân biệt A, B, C, D đồng phẳng đồng phẳng

5. Phân tích một vectơ theo ba vectơ không đồng phẳng

Định lí

Cho ba vectơ và   không đồng phẳng. Với mọi vectơ , ta đều tìm được duy nhất một bộ số (m; n; p) sao cho

Hình ảnh minh họa

6. Tích vô hướng của hai vectơ

Định nghĩa

a) Nếu  và thì

b) Nếu  hoặc thì

c) Bình phương vô hướng của một vectơ:

Một số ứng dụng của tích vô hướng 

a) Nếu  và ta có

b) Công thức tính cosin của góc hợp bởi hai vectơ khác vectơ:

c) Công thức tính độ dài của một đoạn thẳng: