Trong mặt phẳng Oxy cho điểm M(2; 3). Điểm M là ảnh của điểm nào trong bốn điểm sau qua phép đối xứng trục Oy?
Phép đối xứng trục Oy có:
Suy ra
Vậy ảnh của điểm M(2; 3) qua phép đối xứng trục Oy là D(-2; 3).
Trong các mệnh đề sau mệnh đề nào đúng?
Phương án "Tam giác đều có vô số trục đối xứng" sai vì tam giác đều chỉ có ba trục đối xứng là ba đường cao.
Phương án "Một hình có vô số trục đối xứng thì hình đó phải là đường tròn" sai vì đường thẳng cũng có vô số trục đối xứng (là đường thẳng bất kì vuông góc với đường thẳng đã cho).
Phương án "Hình gồm hai đường thẳng vuông góc có vô số trục đối xứng" vì hình gồm hai đường thẳng vuông góc có bốn trục đối xứng (là chính hai đường thẳng đó và hai đường phân giác của góc tạo bởi hai đường thẳng đó).
Phương án "Hình tròn có vô số trục đối xứng" đúng vì trục đối xứng là 1 đường thẳng bất kì đi qua tâm đường tròn.
Trong mặt phẳng, hình vuông có mấy trục đối xứng?
Hình vuông có 4 trục đối xứng
Hình vẽ minh họa
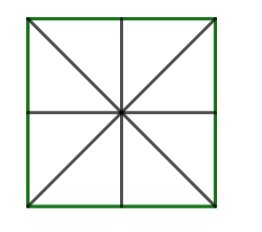
Trong mặt phẳng, hình nào sau đây có trục đối xứng?
Tam giác cân có trục đối xứng là đường cao (cũng là trung trực, phân giác).
Trong mặt phẳng, cho hình thang cân 
có . Tìm mệnh đề đúng:
Hình vẽ minh họa
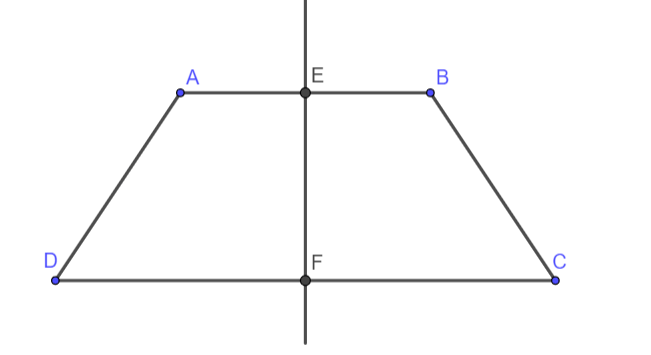
Gọi E, F lần lượt là trung điểm của AB và CD
Khi đó B đối xứng với A qua EF và C đối xứng với D qua EF
Vậy ta có phép đối xứng với trục biến DA thành CB nên
Trong mặt phẳng cho hai đường thẳng a và b tạo với nhau góc . Có bao nhiêu phép đối xứng trục biến a thành b.
Hình vẽ minh họa
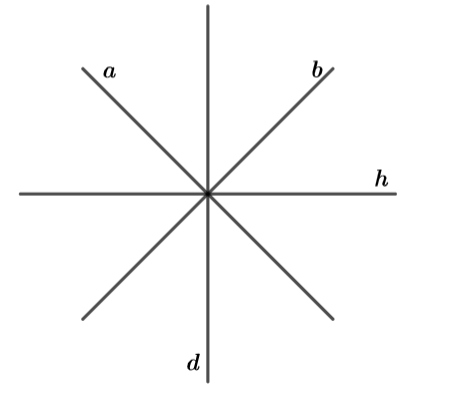
Có hai phép đối xứng trục biến đường thẳng a thành đường thẳng b
Trục đối xứng là hai đường phân giác của góc tạo bởi a và b.
Có bao nhiêu phép đối xứng trục biến một hình chữ nhật thành chính nó?
Có hai phép đối xứng trục biến một hình chữ nhật thành chính nó.
Trục đối xứng là hai đường thẳng đi qua tâm hình chữ nhật và vuông góc với hai cặp cạnh đối diện của nó.
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y - 2 = 0. Phép đối xứng trục Oy biến d thành d’ có phương trình:
Phép đối xứng trục Oy biến đường thẳng d thành đường thẳng d'.
Biến mỗi điểm M(x, y) thuộc d thành điểm M'(x'; y') thuộc d'.
Áp dụng biểu thức tọa độ của phép đối xứng trục Oy ta có:
Vì điểm M(x, y) thuộc đường thẳng d nên:
=> hay
Do đó, phương trình đường thẳng d' là:
Trong mặt phẳng Oxy cho parabol (P) có phương trình: . Phép đối xứng trục Ox biến (P) thành (P’) có phương trình:
Phép đối xứng trục Ox, biến parabol (P) thành parabol (P') và biến mỗi điểm M(x, y) thuộc (P) thành điểm M'(x'; y') thuộc (P')
Áp dụng biểu thức tọa độ của phép đối xứng trục Ox ta có:
Vì điểm M thuộc (P) nên
=>
=>
Suy ra, phương trình (P') là:
Có bao nhiêu phép đối xứng trục biến một đường thẳng d cho trước thành chính nó.
Gọi d' là đường thẳng vuông góc với đường thẳng d.
Khi đó, phép đối xứng trục d' biến d thành chính nó.
Có vô số đường thẳng d' vuông góc với d nên có vô số phép đối xứng trục biến một đường thẳng d cho trước thành chính nó.
Cho hai đường thẳng vuông góc với nhau a và b. Có bao nhiêu phép đôi xứng trục biến a thành a và b thành b?
Qua trục đối xứng là đường thẳng a sẽ biến a thành a và biến b thành b.
Qua trục đối xứng là đường thẳng b sẽ biến a thành a và biến b thành b.
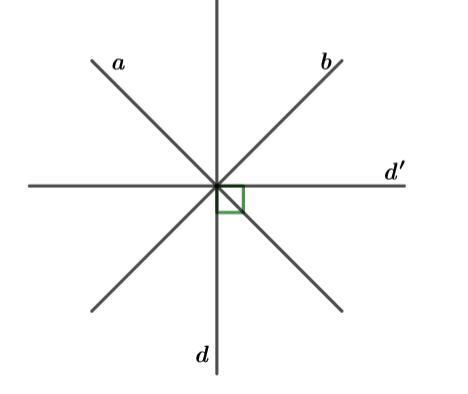
Hình gồm hai đường thẳng d và d' vuông góc với nhau có mấy trục đối xứng?
Hình có hai trục đối xứng, đó là các đường thẳng a, d', a và b
Trong đó a và b là các đường phân giác của góc tạo bởi hai đường thẳng d à d'
Hình vẽ minh họa
Cho hai đường thẳng a và b cắt nhau và góc ở giữa chúng bằng 60∘. Có bao nhiêu phép đối xứng trục biến a thành a và b thành b?
Để biến a thành a thì trục đối xứng trùng với a hoặc vuông góc với a.
Trường hợp 1: Trục đối xứng trùng với a mà a tạo với b góc 600 => a không là trục đối xứng để biến b thành b.
Trường hợp 2: Trục đối xứng vuông góc với a mà a tạo với b góc 600 => đường thẳng đó không là trục đối xứng để biến b thành b.
Cho hai đường thẳng song song d và d'. Có bao nhiêu phép đối xứng trục biến mỗi đường thẳng thành chính nó?
Đường thẳng Δ vuông góc với d và d' sẽ biến d và d' thành chính nó.
Có vô số đường thẳng Δ vuông góc với d và d'.
Cho hai đường thẳng song song d và d'. Có bao nhiêu phép đối xứng trục biến đường thẳng d thành đường thẳng d'?
Khi 2 đường thẳng d và d' song song thì có 1 phép đối xứng trục biến d thành d'.
Trục đối xứng là đường thẳng song song và cách đều 2 đường thẳng d và d'.
