Bất phương trình bậc nhất hai ẩn sách CTST

Ví dụ:

2. Nghiệm của bất phương trình bậc nhất hai ẩn

Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm.

Ví dụ: Cặp số là một nghiệm của bất phương trình vì

3. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn

Trong mặt phẳng tọa độ , tập hợp các điểm sao cho  được gọi là miền nghiệm của bất phương trình .

Biểu diễn miền nghiệm của bất phương trình

Bước 1: Trên mặt phẳng , vẽ đường thẳng

Bước 2: Lấy một điểm không thuộc . Tính

Bước 3: Kết luận

• Nếu thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ ) chứa điểm .
• Nếu thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ ) không chứa điểm .

Chú ý

Nếu ta thường chọn là gốc tọa độ.

Nếu ta thường chọn có tọa độ hoặc .

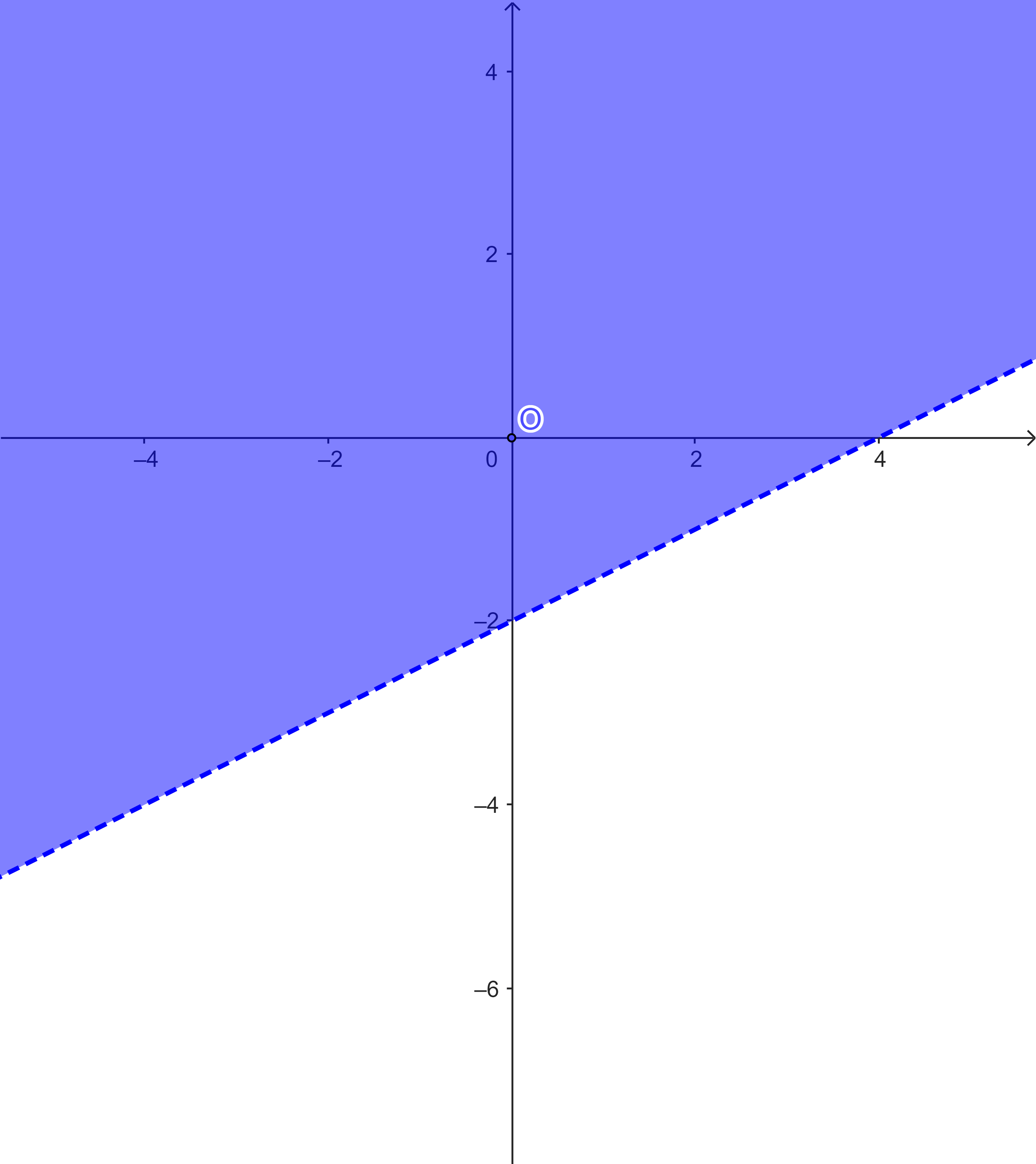
Ví dụ: Biểu diễn hình học tập nghiệm của bất phương trình bậc nhất hai ẩn .

Hướng dẫn giải

Vẽ đường thẳng .

Thay tọa độ điểm vào vế trái phương trình đường thẳng , ta được: .

Vậy miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm . (Trên hình là nửa mặt phẳng tô màu).