Lớp 10 Toán 10 - Chân trời sáng tạo

Khái niệm Vectơ sách CTST

A. Định nghĩa, xác định vectơ

Định nghĩa Vectơ

Vectơ là một đoạn thẳng có hướng nghĩa là đã chỉ ra điểm đầu và điểm cuối.

  • Vectơ có điểm đầu (gốc) A, điểm cuối (ngọn) B được kí hiệu là: \overrightarrow {AB}.
  • Vectơ còn được kí hiệu là \overrightarrow a ,\overrightarrow b ,\overrightarrow x ,\overrightarrow y ,... khi không có điểm đầu và điểm cuối của nó.
  • Hình vẽ minh họa

Khái niệm vectơ

  • Một vectơ hoàn toàn được xác định khi biết điểm đầu và điểm cuối của nó.
  • Đường thẳng đi qua hai điểm A và B được gọi là giá của vectơ \overrightarrow {AB}.

Chú ý

Với hai điểm phân biệt A và B ta chỉ có một đoạn thẳng (AB hoặc BA) nhưng có hai vectơ khác nhau là: \overrightarrow {AB} và \overrightarrow {BA}.

Độ dài vectơ

Độ dài của đoạn thẳng AB là độ dài (hay mô – đun) của vectơ \overrightarrow {AB}, kí hiệu là \left| {\overrightarrow {AB} } \right|, tức là AB = \left| {\overrightarrow {AB} } \right|.

Đương nhiên \left| {\overrightarrow {BA} } \right| = \left| {\overrightarrow {AB} } \right|.

Ví dụ: Cho hình vuông ABCD cạnh a. Gọi M là trung điểm của AB, N là điểm đối xứng với C qua D. Hãy tính độ dài của vectơ \overrightarrow {MD} ;\overrightarrow {MN}.

Hướng dẫn giải

Hình vẽ minh họa

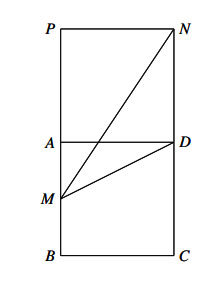
Khái niệm vectơ

Áp dụng định lý Py – ta - go trong tam giác vuông MAD ta có:

\begin{matrix} D{M^2} = A{M^2} + A{D^2} \hfill \\ \Rightarrow D{M^2} = {\left( {\dfrac{a}{2}} \right)^2} + {a^2} = \dfrac{{5{a^2}}}{4} \hfill \\ \Rightarrow DM = \dfrac{{a\sqrt 5 }}{2} \hfill \\ \Rightarrow MD = \left| {\overrightarrow {MD} } \right| = \dfrac{{a\sqrt 5 }}{2} \hfill \\ \end{matrix}

Qua N kẻ đường thẳng song song với AD cắt AB tại P.

Khi đó tứ giác ADNP là hình vuông và PM = PA + AM = a + \frac{a}{2} = \frac{{3a}}{2}

Áp dụng định lý Py – ta - go trong tam giác vuông NPM ta có:

\begin{matrix} M{N^2} = N{P^2} + P{M^2} \hfill \\ \Rightarrow M{N^2} = {a^2} + {\left( {\dfrac{{3a}}{2}} \right)^2} = \dfrac{{13{a^2}}}{4} \hfill \\ \Rightarrow MN = \dfrac{{a\sqrt {13} }}{2} \hfill \\ \Rightarrow MN = \left| {\overrightarrow {MN} } \right| = \dfrac{{a\sqrt {13} }}{2} \hfill \\ \end{matrix}

B. Hai vectơ cùng phương, cùng hướng

Định nghĩa Phương, hướng vectơ

Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

Cho hình vẽ

Khai niệm vectơ

Trên hình 1.3a) ta có \overrightarrow {AB} ,\overrightarrow {CD} ,\overrightarrow {EF} các vectơ cùng phương.

Trên hình 1.3b) ta có: \overrightarrow {AB} và \overrightarrow {MN} cùng phương còn \overrightarrow {AB} và \overrightarrow {MP} không cùng phương.

  • Hai vectơ cùng phương có thể cùng hướng hoặc ngược hướng.

Chẳng hạn \overrightarrow {AB} và \overrightarrow {CD} cùng hướng, \overrightarrow {AB} và \overrightarrow {EF} ngược hướng (Hình 1.3a).

  • Ba điểm A, B, C thẳng hàng khi và chỉ khi hai vectơ \overrightarrow {AB} và \overrightarrow {AC} cùng phương.

Hình vẽ minh họa

Khái niệm vectơ

Chú ý

Khi nó hai vectơ cùng hướng hay ngược hướng thì chúng đã cùng phương.

Ví dụ: Cho hình vẽ:

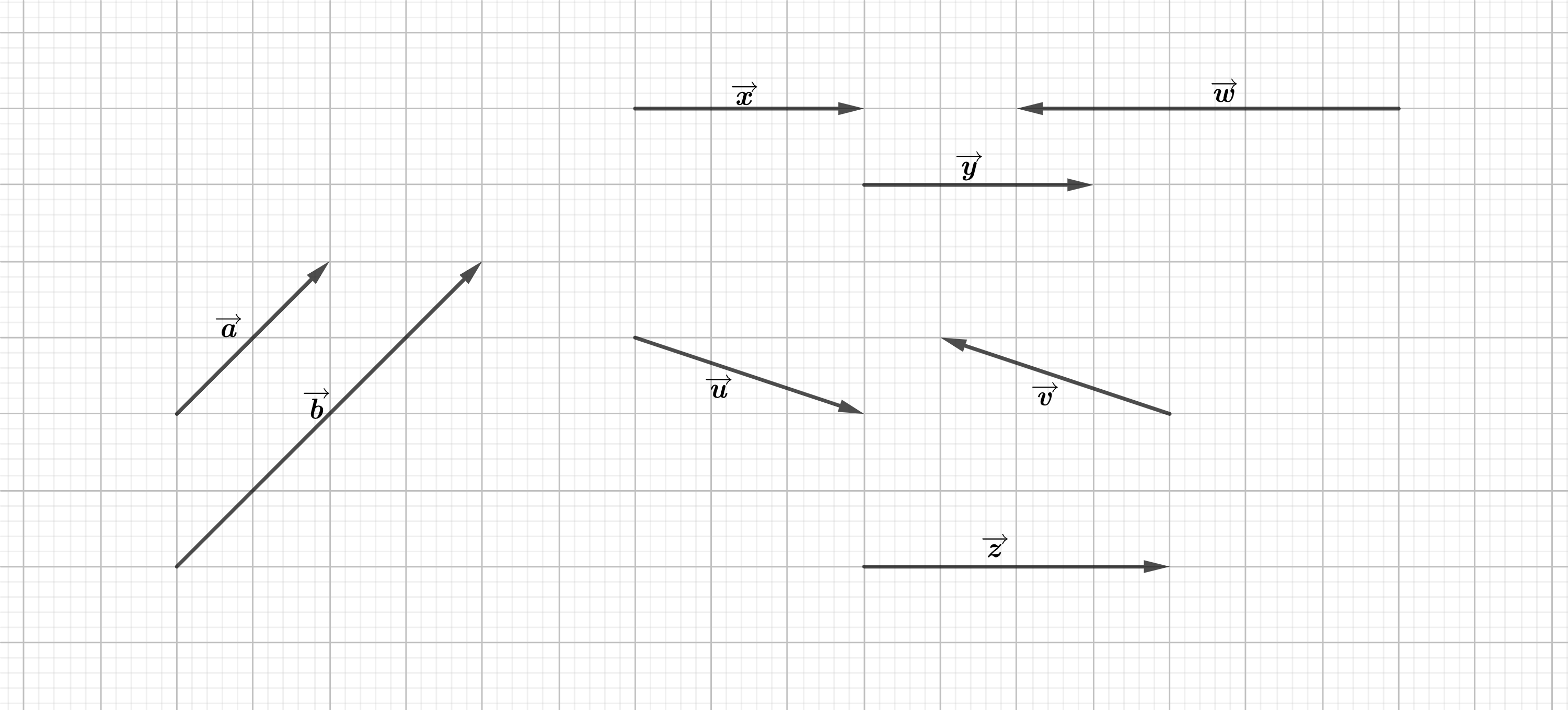
Khái niệm vectơ

Hãy chỉ ra các vectơ cùng phương, cùng hướng, ngược hướng và các vectơ bằng nhau.

Hướng dẫn giải

Các vectơ cùng phương: \overrightarrow a và \overrightarrow b, \overrightarrow u và \overrightarrow v, \overrightarrow x ,\overrightarrow y ,\overrightarrow z và \overrightarrow w.

Các vectơ cùng hướng: \overrightarrow a và \overrightarrow b, \overrightarrow x ,\overrightarrow y và \overrightarrow z.

Các vectơ ngược hướng: \overrightarrow u và \overrightarrow v, \overrightarrow w và \overrightarrow x, \overrightarrow w và \overrightarrow y, \overrightarrow w và \overrightarrow z.

Các vectơ bằng nhau: \overrightarrow x = \overrightarrow y.

C. Vectơ - không

Định nghĩa

Vectơ - không là vectơ có điểm đầu và điểm cuối trùng nhau. Vectơ - không được kí hiệu là \overrightarrow 0.

Ví dụ: \overrightarrow 0 = \overrightarrow {AA} = \overrightarrow {BB} = ...

Chú ý

  • Quy ước vectơ – không có độ dài bằng 0.
  • Vectơ – không luôn cùng phương, cùng hướng với mọi vectơ.
  • Vectơ đối của vectơ – không là chính nó.

D. Vectơ bằng nhau – Vectơ đối nhau

Định nghĩa

  • Hai vectơ  \overrightarrow a và \overrightarrow b được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài. Kí hiệu: \overrightarrow a = \overrightarrow b
  • Hai vectơ \overrightarrow a và \overrightarrow b được gọi là đối nhau nếu chúng ngược hướng và có cùng độ dài. Kí hiệu: \overrightarrow a = - \overrightarrow b ta nói vectơ \overrightarrow b là vectơ đối của vectơ \overrightarrow a.

Ví dụ: Cho hình bình hành ABCD như hình vẽ:

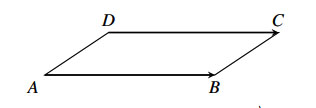
Khái niệm vectơ

Ta có: \left\{ {\begin{array}{*{20}{c}} {\overrightarrow {AB} = \overrightarrow {DC} ,\overrightarrow {AD} = \overrightarrow {BC} } \\ {\overrightarrow {AB} = - \overrightarrow {CD} ,\overrightarrow {AD} = - \overrightarrow {CB} } \end{array}} \right.

Chú ý

Khi cho trước vectơ \overrightarrow a và điểm O thì ta luôn tìm được một điểm A duy nhất sao cho \overrightarrow {OA} = \overrightarrow a. Nếu I là trung điểm của đoạn thẳng AB thì \overrightarrow {AI} = \overrightarrow {IB}.

Ví dụ: Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm AB, BC, CD, DA. Chứng minh \overrightarrow {MN} = \overrightarrow {QP}.

Hướng dẫn giải

Hình vẽ minh họa

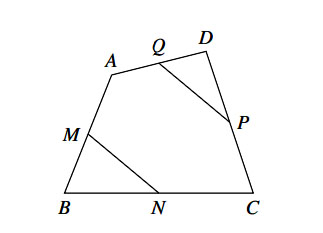
Khái niệm vectơ

Do M, N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC

=> \left\{ {\begin{array}{*{20}{c}} {MN//AC} \\ {MN = \dfrac{1}{2}AC} \end{array}} \right. (1).

Tương tự, QP là đường trung bình của tam giác ADC

=> \left\{ {\begin{array}{*{20}{c}} {QP//AC} \\ {QP = \dfrac{1}{2}AC} \end{array}} \right. (2).

Từ (1) và (2) suy ra \overrightarrow {MN} = \overrightarrow {QP}.

Câu trắc nghiệm mã số: 21099,21096,21094
  • 79 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 10 CTST