Lớp 10 Toán 10 - Chân trời sáng tạo

Hàm số bậc hai sách CTST

1. Hàm số bậc hai

Định nghĩa

Hàm số bậc hai cho bởi công thức dạng y = f(x) = a{x^2} + bx + c với a,b,c \in \mathbb{R};a \ne 0.

Tập xác định của hàm số này là: D=\mathbb{R}.

2. Đồ thị hàm số bậc hai

Định lí

Đồ thị hàm số bậc hai y = f(x) = a{x^2} + bx + c ,(a \ne 0) là một đường parabol có đỉnh là điểm I\left( { - \frac{b}{{2a}};\frac{{ - \Delta }}{{4a}}} \right), có trục đối xứng là đường thẳng x = - \frac{b}{{2a}}. Parabol này quay bề lõm lên trên nếu a > 0, quay xuống dưới nếu a < 0.

Cách vẽ đồ thị hàm số bậc hai

Bước 1: Xác định đỉnh I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)

Bước 2: Vẽ trục đối xứng x = - \frac{b}{{2a}}

Bước 3: Lập bảng giá trị

x {x_1} {x_2} - \frac{b}{{2a}}  {x_3} {x_4}
y y\left( {{x_1}} \right) y\left( {{x_2}} \right) - \frac{\Delta }{{4a}} y\left( {{x_3}} \right) y\left( {{x_4}} \right)

Chú ý

  • Đồ thị của hàm số y = f(x) = a{x^2} + bx + c ,(a \ne 0) cắt trục tung tại điểm (0; c).
  • Đồ thị của hàm số y = f(x) = a{x^2} + bx + c ,(a \ne 0) cắt trục hoành (nếu có) tại điểm có tọa độ (x_0; 0) với x_0 là nghiệm của phương trình ax^2 +bx+c = 0. 

Bước 4: Vẽ parabol.

Chú ý: Khi vẽ cần chú ý đến dấu của hệ số a (a > 0 bề lõm quay lên trên, a < 0 bề lõm quay xuống dưới).

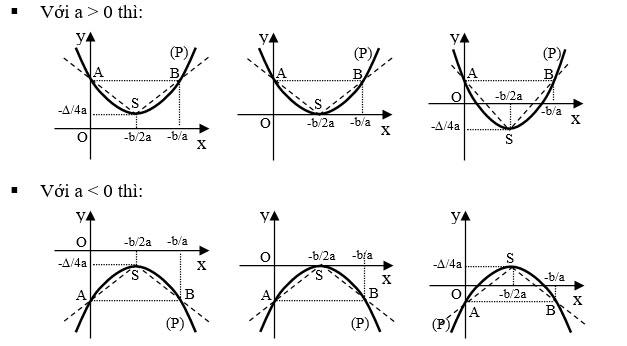
Hàm số bậc hai

3. Sự biến thiên của hàm số bậc hai

Dựa vào đồ thị của hàm số y = f(x) = a{x^2} + bx + c ,(a \ne 0), ta có bảng biến thiên của nó trong hai trường hợp a > 0 và a<0 như sau:
Với a > 0 ta có:

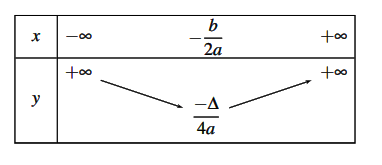
Hàm số bậc hai

Với a<0 ta có:

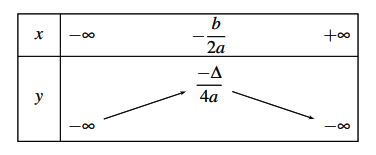
Hàm số bậc hai

Định lí

  • Nếu a > 0 thì hàm số y = f(x) = a{x^2} + bx + c nghịch biến trên khoảng \left( { - \infty ;- \frac{b}{{2a}}} \right), đồng biến trên khoảng \left( { - \frac{b}{{2a}}; + \infty } \right)
  • Nếu a<0 thì hàm số y = f(x) = a{x^2} + bx + c đòng biến trên khoảng \left( { - \infty ;- \frac{b}{{2a}}} \right), nghịch biến trên khoảng \left( { - \frac{b}{{2a}}; + \infty } \right)

Ví dụ: Lập bảng biến thiên và vẽ đồ thị của hàm số y=x^2-2x.

Hướng dẫn giải

Ta có a = 1,b = −2, c = 0. Suy ra tọa độ đỉnh là I(1;-1).

Vậy bảng biến thiên là 

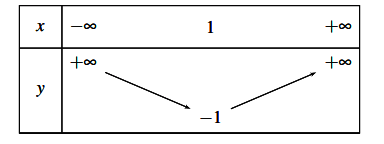
Hàm số bậc hai

=> Hàm số nghịch biến trên khoảng (−∞; 1) và đồng biến trên khoảng (1;+∞).

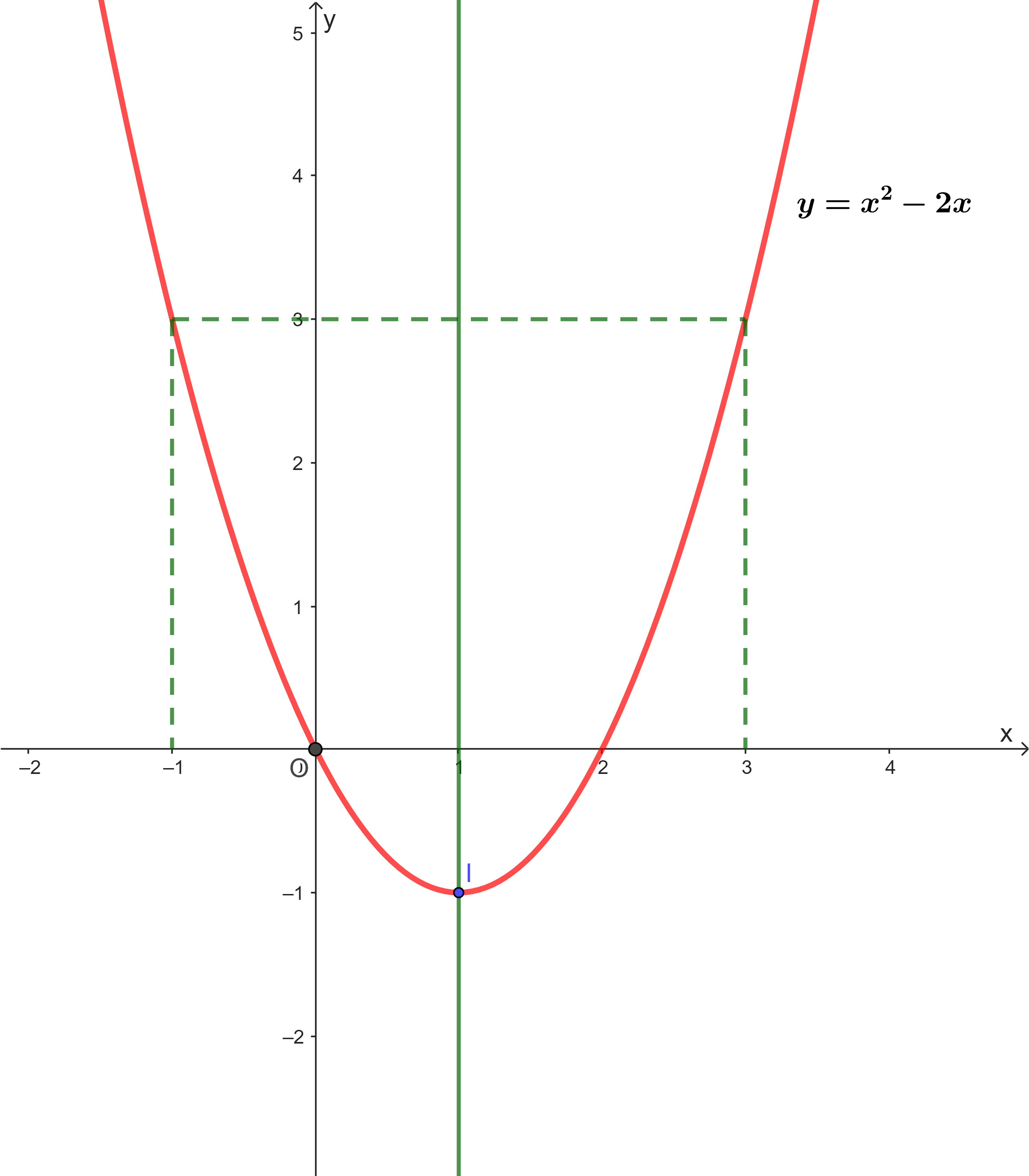
Vẽ đồ thị:

Ta có đỉnh là I(1;-1) và trục đối xứng là x=1.

Bảng giá trị

x

-1

0

1

2

3

y

3

0

-1

0

3

Ta có đồ thị của hàm số y = x^2 −2x là 

Hàm số bậc hai

4. Phương trình hoành độ giao điểm

Cho hàm số y=f(x) có đồ thị là (C_1) và hàm số y=g(x) có đồ thị là (C_2). Khi đó nếu M(x;y) là giao điểm của (C_1) và (C_2) thì tọa độ của M là nghiệm của hệ phương trình:

\left\{ {\begin{array}{*{20}{c}} {y = f\left( x \right)} \\ {y = g\left( x \right)} \end{array}} \right. \Rightarrow f\left( x \right) = g\left( x \right) (*)

Phương trình (*) được gọi là phương trình hoành độ giao điểm của hai đồ thị (C_1) và (C_2). 

Để giải một bài toán về tính chất giao điểm của hai đồ thị (C_1) và (C_2) ta có thể tiến hành theo các bước như sau:

  • Lập phương trình hoành độ giao điểm của hai đồ thị (C_1) và (C_2).
  • Biến đổi phương trình về dạng bậc hai đơn giản.
  • Dựa vào điều kiện ban đầu của bài toán để chuyển về điều kiện cho phương trình hoành độ giao điểm.

5. Định lí Vi - ét

Định lí

Cho phương trình bậc hai a{x^2} + bx + c = 0;\left( {a \ne 0} \right)

a) Nếu phương trình bậc hai có hai nghiệm {x_1},{x_2} thì ta có: \left\{ {\begin{array}{*{20}{c}} {S = {x_1} + {x_2} = - \dfrac{b}{a}} \\ {P = {x_1}.{x_2} = \dfrac{c}{a}} \end{array}} \right..

b) Phương trình có hai nghiệm trái dấu khi và chỉ khi P<0.

c) Phương trình có hai nghiệm dương phân biệt khi và chỉ khi: \left\{ {\begin{array}{*{20}{c}} {\Delta > 0} \\ {S > 0} \\ {P > 0} \end{array}} \right..

d) Phương trình có hai nghiệm âm phân biệt khi và chỉ khi: \left\{ {\begin{array}{*{20}{c}} {\Delta > 0} \\ {S < 0} \\ {P > 0} \end{array}} \right..

e) Phương trình có hai nghiệm phân biệt khác x_0 khi và chỉ khi \left\{ {\begin{array}{*{20}{c}} {\Delta > 0} \\ {a{x_0}^2 + b{x_0} + c \ne 0} \end{array}} \right..

6. Ứng dụng của hàm số bậc hai

Tầm bay cao và tầm bay xa

Chọn điểm (0;{y_0}) là điểm xuất phát thì phương trình quỹ đạo của cầu lông khi rời mặt vợt là:

y = \frac{{ - g.{x^2}}}{{2.{v_0}^2.{{\cos }^2}\alpha }} + \tan \alpha .x + {y_0}

Trong đó:

g là giá tốc trọng trường ( \approx 9,8\;m/{s^2})

\alpha là góc phát cầu (so với phương ngang của mặt đất)

{v_0} là vận tốc ban đầu của cầu

{y_0} là khoảng cách từ vị trí phát cầu đến mặt đất

Quỹ đạo chuyển động của cầu lông là một parabol.

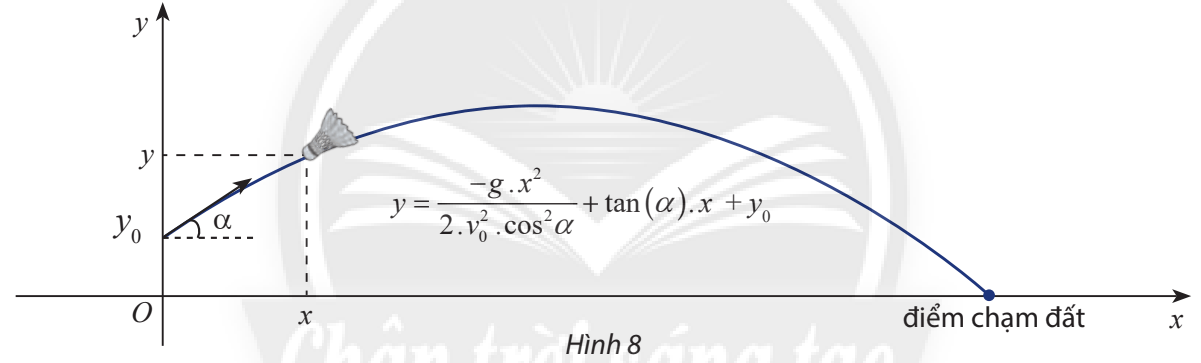
Ứng dụng của hàm số bậc hai

Vị trí cao nhất tại đỉnh parabol, gọi là tầm bay cao;

Khoảng cách từ nơi đứng phát cầu đến điểm chạm đất, gọi là tầm bay xa.

Câu trắc nghiệm mã số: 7905,27607,27605
  • 127 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 10 CTST