Lớp 10 Toán 10 - Chân trời sáng tạo

Luyện tập Hàm số và đồ thị

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 10 câu
  • Điểm số bài kiểm tra: 10 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu làm bài
00:00:00
  • Câu 1: Nhận biết
    Hàm số nghịch biến

    Trong các hàm số sau, hàm số nào là nghịch biến:

    Hướng dẫn:

    Ta có: 

    Hàm số y = f(x) = -2x + 2 có a = -2 < 0

    => Hàm số nghịch biến.

  • Câu 2: Nhận biết
    Tìm tập xác định của hàm số

    Tập xác định của hàm số y = f(x) = 2\sqrt{x} ‒ 1 là:

    Hướng dẫn:

    Điều kiện xác định của hàm số y = f(x) = 2\sqrt{x} ‒ 1 là:

    x \geqslant 0

    => Tập xác định của hàm số là: D = [0; +∞)

  • Câu 3: Vận dụng
    Xác định đồ thị của hàm số y=|2x+3|

    Đồ thị hàm số y = |2x + 3| là hình nào trong các hình sau:

    Hướng dẫn:

    Tập xác định của hàm số D = \mathbb{R}

    Ta có: y = \left| {2x + 3} ight| = \geqslant \left\{ {\begin{array}{*{20}{c}}{2x + 3{\text{ khi }}x \geqslant - \frac{3}{2}} \\{ - 2x - 3{\text{ khi }}x < - \frac{3}{2}}\end{array}} ight.

    Ta vẽ đồ thị y = 2x + 3 với {x \geqslant - \frac{3}{2}} (d_1)

    Ta có bảng sau:

    x

    0

    - \frac{3}{2}

    y = f(x)

    3

    0

    Suy ra đồ thị hàm số y = f(x) = 2x + 3 với {x \geqslant - \frac{3}{2}} là phần đồ thị nằm bên trên trục Ox và đi qua các điểm A(- \frac{3}{2}; 0) và B(0; 3).

    Ta có đồ thị như sau:

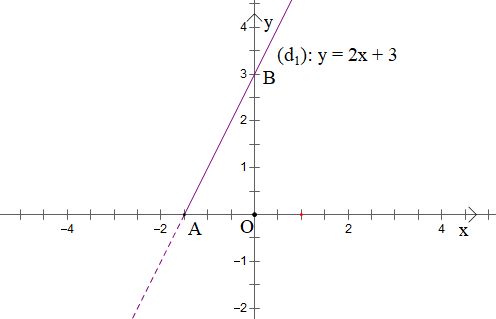
    Xác định đồ thị của hàm số

    Tương tự ta có đồ thị hàm số y = f(x) = - 2x - 3 với x <- \frac{3}{2} là phần đồ thị nằm bên trên trục Ox và đi qua các điểm C(-2; 1) và D(-3; 3).

    Kết hợp 2 đồ thị ta có đồ thị hàm số y = |2x + 3| là phần đồ thị nét liền nằm trên trục Ox.

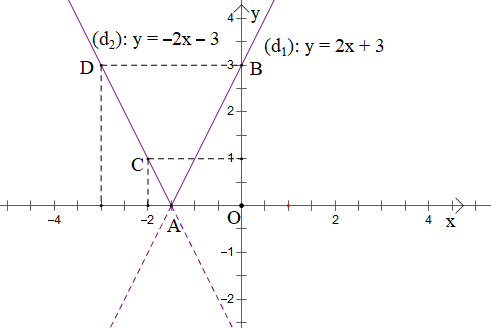
    Xác định đồ thị của hàm số

  • Câu 4: Nhận biết
    Chọn khẳng định sai

    Cho hàm số y = f(x) = |-5x|. Khẳng định nào sau đây là sai?

    Hướng dẫn:

    Ta có: f(\frac{1}{5})=|-5.\frac{1}{5}|=1 e-1

    Khẳng định sai là: f(\frac{1}{5})=-1

  • Câu 5: Nhận biết
    Điền vào chỗ trống

    Điền vào chỗ trống: Hàm số y = f(x) xác định trên khoảng (a; b) có thể là hàm số ….

    Hướng dẫn:

    Hàm số y = f(x) xác định trên khoảng (a; b) có thể là hàm số đồng biến hoặc nghịch biến

  • Câu 6: Thông hiểu
    Tìm tập xác định của hàm số

    Tìm tập xác định của hàm số y=\sqrt{x+2}-\frac{2}{x-3}

    Hướng dẫn:

    Điều kiện xác định của hàm số là: \left\{ {\begin{array}{*{20}{c}} {x + 2 \geqslant 0} \\ {x - 3 e 0} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x \geqslant - 2} \\ {x e 3} \end{array}} ight.

    => Tập xác định của hàm số là: D = \left[ {2; + \infty } ight)\backslash \left\{ 3 ight\}

  • Câu 7: Vận dụng
    Hàm số nào tăng trên khoảng (-1;0)

    Trong các hàm số sau, hàm số nào tăng trên khoảng (-1;0)?

    Hướng dẫn:

    Lấy hai điểm x_1,x_2\in (-1;0) sao cho - 1 < {x_1} < {x_2} < 0 khi đó {x_2} - {x_1} > 0

    Xét đáp án y = x ta có: 

    \begin{matrix} \dfrac{{f\left( {{x_2}} ight) - f\left( {{x_1}} ight)}}{{{x_2} - {x_1}}} = \dfrac{{{x_2} - {x_1}}}{{{x_2} - {x_1}}} = 1 > 0 \hfill \\ \forall {x_1},{x_2} \in \left( { - 1;0} ight) \hfill \\ \end{matrix}

    Vậy hàm số tăng trên (-1,0).

    Xét đáp án y=\frac{1}{x} ta có: 

    \begin{matrix} \dfrac{{f\left( {{x_2}} ight) - f\left( {{x_1}} ight)}}{{{x_2} - {x_1}}} = \dfrac{{\dfrac{1}{{{x_2}}} - \dfrac{1}{{{x_1}}}}}{{{x_2} - {x_1}}} = - \dfrac{1}{{{x_2}.{x_1}}} < 0 \hfill \\ \forall {x_1},{x_2} \in \left( { - 1;0} ight) \hfill \\ \end{matrix}

    Vậy hàm số không tăng trên (-1,0).

    Xét đáp án y = |x| ta có: 

    \begin{matrix} \dfrac{{f\left( {{x_2}} ight) - f\left( {{x_1}} ight)}}{{{x_2} - {x_1}}} = \dfrac{{\left| {{x_2}} ight| - \left| {{x_1}} ight|}}{{{x_2} - {x_1}}} = \dfrac{{ - {x_2} + {x_1}}}{{{x_2} - {x_1}}} = - < 0 \hfill \\ \forall {x_1},{x_2} \in \left( { - 1;0} ight) \hfill \\ \end{matrix}

    Vậy hàm số không tăng trên (-1,0).

    Xét đáp án y=x^{2} ta có: 

    \begin{matrix} \dfrac{{f\left( {{x_2}} ight) - f\left( {{x_1}} ight)}}{{{x_2} - {x_1}}} = \dfrac{{{{\left( {{x_2}} ight)}^2} - {{\left( {{x_1}} ight)}^2}}}{{{x_2} - {x_1}}} = \left( {{x_2} - {x_1}} ight) < 0 \hfill \\ \forall {x_1},{x_2} \in \left( { - 1;0} ight) \hfill \\ \end{matrix}

    Vậy hàm số không tăng trên (-1,0).

  • Câu 8: Thông hiểu
    Tính tỉ lệ biết chữ của phụ nữ

    Theo tài liệu dân số và phát triển của Tổng cục dân số và kế hoạch hóa gia đình thì:

    Dựa trên số liệu về dân số, kinh tế, xã hội của 85 nước trên thế giới, người ta xây dựng được hàm nêu lên mối quan hệ giữa tuổi thọ trung bình của phụ nữ (y) và tỷ lệ biết chữ của họ (x) như sau: y = 47,17 + 0,307x. Trong đó y là số năm (tuổi thọ), x là tỷ lệ phần trăm biết chữ của phụ nữ. Theo báo cáo của Bộ Giáo dục và Đào tạo năm học 2015 ‒ 2016, tỷ lệ biết chữ đã đạt 96,83% trong nhóm phụ nữ Việt Nam tuổi từ 15 đến 60. Hỏi với tỉ lệ biết chữ của phụ nữ Việt Nam như trên thì nhóm này có tuổi thọ bao nhiêu?

    Hướng dẫn:

    Thay x = 96,83 vào công thức y = 47,17 + 0,307x ta được:

    y = 47,17 + 0,307. 96,83 = 47,17 + 29,72 = 76,89 (năm)

    Vậy nhóm này có tuổi thọ 76,89 tuổi.

  • Câu 9: Thông hiểu
    Tìm x

    Cho hàm số: y = f(x) = |2x-3|. Tìm x để f(x) = 3

    Hướng dẫn:

    Ta có:

    \begin{matrix} f\left( x ight) = 3 \hfill \\ \Leftrightarrow \left| {2x - 3} ight| = 3 \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {2x - 3 = 3} \\ {2x - 3 = - 3} \end{array}} ight. \hfill \\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 3} \\ {x = 0} \end{array}} ight. \hfill \\ \end{matrix}

    Vậy x = 3 hoặc x = 0

  • Câu 10: Nhận biết
    Chọn đáp án đúng

    Hàm số đồng biến thì đồ thị của nó có dạng như thế nào?

    Hướng dẫn:

    Hàm số đồng biến thì đồ thị của nó có dạng đi lên từ trái sang phải

0/10
10 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (50%):
    2/3
  • Thông hiểu (30%):
    2/3
  • Vận dụng (20%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
Làm lại
  • 14 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 10 CTST

Đăng nhập