Lớp 10 Toán 10 - Chân trời sáng tạo

Tích vô hướng của hai vectơ sách CTST

A. Góc giữa hai vectơ

Định nghĩa

Cho hai vectơ \overrightarrow a và \overrightarrow b đều khác vectơ \overrightarrow 0. Từ một điểm O bất kỳ, ta vẽ\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b

Góc \widehat {AOB} với số đo từ 00 đến 1800 được gọi là góc giữa hai vectơ \overrightarrow a và \overrightarrow b.

Ta ký hiệu góc giữa hai vectơ \overrightarrow a và \overrightarrow b là \left( {\overrightarrow a ,\overrightarrow b } \right).

Hình vẽ minh họa

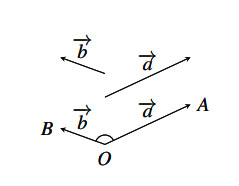
Tích vô hướng của hai vectơ

Chú ý

  • Nếu \left( {\overrightarrow a ,\overrightarrow b } \right) = {90^0} thì ta nói rằng \overrightarrow a và \overrightarrow b vuông góc với nhau, ký hiệu là \overrightarrow a \bot \overrightarrow b hoặc \overrightarrow b \bot \overrightarrow a.
  • Nếu \overrightarrow a và \overrightarrow b cùng hướng thì \left( {\overrightarrow a ,\overrightarrow b } \right) = {0^0}.
  • Nếu \overrightarrow a và \overrightarrow b ngược hướng thì \left( {\overrightarrow a ,\overrightarrow b } \right) = {180^0}.

B. Tích vô hướng của hai vectơ

Định nghĩa

Cho hai vectơ \overrightarrow a và \overrightarrow b đều khác \overrightarrow 0. Tích vô hướng của \overrightarrow a và \overrightarrow b là một số, kí hiệu là \overrightarrow a .\overrightarrow b, được xác định bởi công thức sau:

\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)

Trường hợp ít nhất một trong hai vectơ \overrightarrow a và \overrightarrow b bằng vectơ \overrightarrow 0 ta quy ước \overrightarrow a .\overrightarrow b = \overrightarrow 0.

a) Với \overrightarrow a và \overrightarrow b khác vectơ ta có: \overrightarrow a .\overrightarrow b = \overrightarrow 0 \Leftrightarrow \overrightarrow a \bot \overrightarrow b.

b) Khi \overrightarrow a = \overrightarrow b tích vô hướng \overrightarrow a .\overrightarrow a được kí hiệu là {\overrightarrow a ^2} và số này được gọi là bình phương vô hướng của vectơ \overrightarrow a. Ta có: {\overrightarrow a ^2} = \left| {\overrightarrow a } \right|.\left| {\overrightarrow a } \right|.\cos \left( {{0^0}} \right) = {\left| {\overrightarrow a } \right|^2}.

Ví dụ: Cho hình vuông ABCD có cạnh bằng 2a\sqrt 2. Tính tích vô hướng của \overrightarrow {AB} .\overrightarrow {AC}.

Hướng dẫn giải

Hình vẽ minh họa

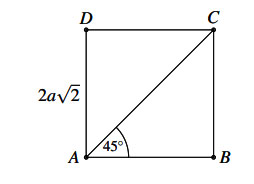
Tích vô hướng của hai vectơ

Ta có: \overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)

Ta có: \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = {45^0} (theo tính chất hình vuông)

Vì tam giác ABC vuông tại A nên A{C^2} = A{B^2} + B{C^2} = 16{a^2}

=> AC = 4a

=> \overrightarrow {AB} .\overrightarrow {AC} = 2a\sqrt 2 .4a.\cos \left( {{{45}^0}} \right) = 8{a^2}

C. Tính chất của tích vô hướng

Tính chất

Với ba vectơ \overrightarrow a ;\overrightarrow b ;\overrightarrow c bất kì và mọi số k ta có:

  • \overrightarrow a .\overrightarrow b = \overrightarrow b .\overrightarrow a (tính chất giao hoán)
  • \overrightarrow a .\left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow a .\overrightarrow b + \overrightarrow a .\overrightarrow c (tính chất phân phối)
  • k.\left( {\overrightarrow a .\overrightarrow b } \right) = \overrightarrow a .\left( {k.\overrightarrow b } \right) = \overrightarrow b .\left( {k.\overrightarrow a } \right)
  • {\overrightarrow a ^2} \geqslant 0;{\overrightarrow a ^2} = 0 \Leftrightarrow \overrightarrow a = \overrightarrow 0

Ví dụ: Cho bốn điểm A, B, C, D bất kì. Chứng minh rằng:

\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} = 0

Hướng dẫn giải

Đẳng thức cần chứng minh tương đương với

\begin{matrix} \overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} \hfill \\ = \overrightarrow {DA} .\left( {\overrightarrow {DC} - \overrightarrow {DB} } \right) + \overrightarrow {DB} .\left( {\overrightarrow {DA} - \overrightarrow {DC} } \right) + \overrightarrow {DC} .\left( {\overrightarrow {DB} - \overrightarrow {DA} } \right) \hfill \\ = \overrightarrow {DA} .\overrightarrow {DC} - \overrightarrow {DA} .\overrightarrow {DB} + \overrightarrow {DB} .\overrightarrow {DA} - \overrightarrow {DB} .\overrightarrow {DC} + \overrightarrow {DC} .\overrightarrow {DB} - \overrightarrow {DC} .\overrightarrow {DA} \hfill \\ = \left( {\overrightarrow {DA} .\overrightarrow {DC} - \overrightarrow {DC} .\overrightarrow {DA} } \right) + \left( { - \overrightarrow {DA} .\overrightarrow {DB} + \overrightarrow {DB} .\overrightarrow {DA} } \right) + \left( { - \overrightarrow {DB} .\overrightarrow {DC} + \overrightarrow {DC} .\overrightarrow {DB} } \right) \hfill \\ = 0 + 0 + 0 \hfill \\ = 0 \hfill \\ \end{matrix}

Nhận xét

Từ các tính chất của tích vô hướng hai vectơ ta suy ra

  • {\left( {\overrightarrow a + \overrightarrow b } \right)^2} = {\overrightarrow a ^2} + 2\overrightarrow a .\overrightarrow b + {\overrightarrow b ^2}
  • {\left( {\overrightarrow a - \overrightarrow b } \right)^2} = {\overrightarrow a ^2} - 2\overrightarrow a .\overrightarrow b + {\overrightarrow b ^2}
  • \left( {\overrightarrow a + \overrightarrow b } \right).\left( {\overrightarrow a - \overrightarrow b } \right) = {\overrightarrow a ^2} - {\overrightarrow b ^2}
Câu trắc nghiệm mã số: 21593,21594,21595,21596
  • 154 lượt xem
Sắp xếp theo
🖼️
Xóa Gửi bình luận

Toán 10 CTST